Politechnika Częstochowska

Wydział Elektryczny

Katedra Elektrotechniki

Zakład Elektrotechniki

Laboratorium Elektrotechniki Teoretycznej

Przebiegi prądów i napięć
w obwodzie z żelazem.

Ferrorezonans napięć i prądów

Częstochowa 2004

1. Cel ćwiczenia

Celem ćwiczenia jest zapoznanie się z przebiegami napięć i prądów w obwodzie zawierającym cewkę z rdzeniem ferromagnetycznym oraz zbadanie zjawisk ferrorezonansu napięć
i prądów w układach złożonych z dławików i kondensatorów.

2. Wiadomości podstawowe

2.1. Przebiegi napięć i prądów w obwodzie z ferromagnetykiem

Obecność ferromagnetyka w obwodzie prądu zmiennego o pobudzeniu napięciowym sinusoidalnie zmiennym powoduje nie tylko dodatkowe straty wiroprądowe i histerezowe, ale również zniekształcenie przebiegu prądu. Jeśli strumień magnetyczny w cewce ma przebieg sinusoidalny

to napięcie na cewce wynosi

natomiast na skutek nieliniowości cewki prąd jest znacznie odkształcony od sinusoidy. Konstrukcję krzywej prądu pokazano na rysunku 1.

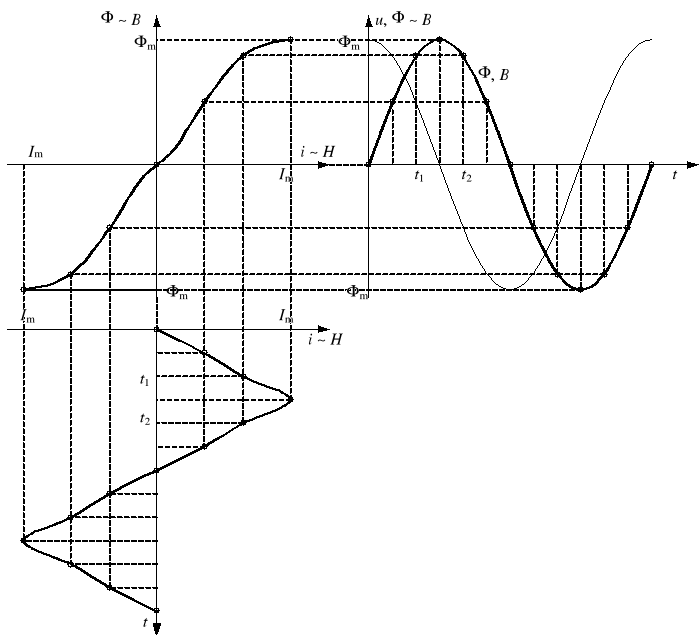
Rys. 1. Konstrukcja krzywej przebiegu prądu w cewce z rdzeniem ferromagnetycznym bez uwzględnienia zjawiska histerezy magnetycznej

Rysujemy charakterystykę magnesowania rdzenia w układzie (H, B). Ponieważ natężenie pola magnetycznego H jest proporcjonalne do prądu i, a indukcja magnetyczna B jest proporcjonalna do strumienia , to przy odpowiednim przeskalowaniu osi H i B otrzymamy charakterystykę magnesowania w układzie (i, ). Po prawej stronie rysujemy przebieg strumienia (t), a pod krzywą magnesowania - układ współrzędnych (i, t), przy czym oś t orientujemy w dół. Dla kolejnych chwil czasu znajdujemy wartość strumienia, a następnie z charakterystyki magnesowania odczytujemy odpowiadający mu prąd i, który zaznaczamy w układzie (i, t). W ten sposób powstaje krzywa prądu.

W rzeczywistości na skutek istnienia zjawiska histerezy magnetycznej krzywa prądu ma nieco inny kształt (rys. 2). Konstruuje się ją podobnie jak poprzednio. Zauważmy, że w zależności od tego, czy strumień rośnie, czy maleje, tej samej wartości strumienia odpowiada inna wartość prądu. Jeśli pętla histerezy jest dostatecznie wąska, to zjawisko histerezy można pominąć i przybliżyć charakterystykę magnesowania podstawową krzywą magnesowania.

Rzeczywista cewka posiada również rezystancję, a więc spadek napięcia na rzeczywistej cewce, jako suma siły elektromotorycznej zaindukowanej w wyniku czasowych zmian strumienia
i spadku napięcia na rezystancji uzwojenia proporcjonalnego do płynącego prądu odkształconego, nie będzie sinusoidalny.

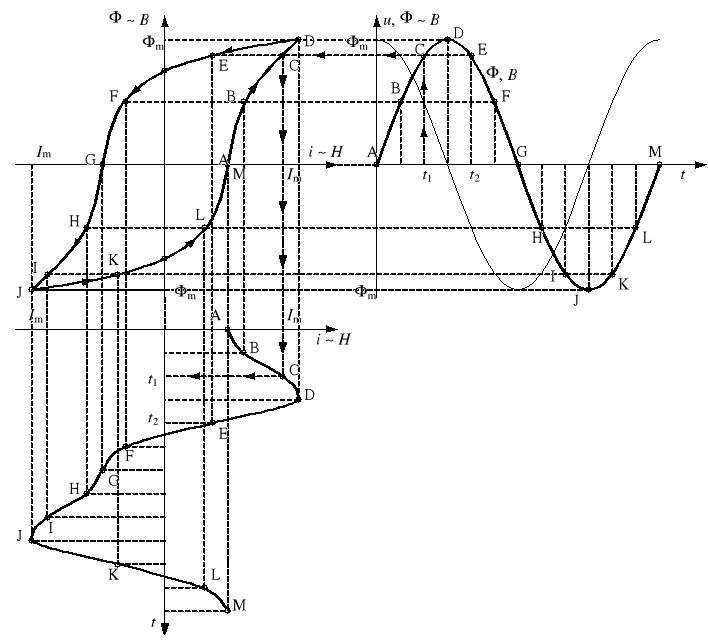
Rys. 2. Konstrukcja krzywej przebiegu prądu w cewce z rdzeniem ferromagnetycznym z uwzględnieniem zjawiska histerezy magnetycznej

2.2. Ferrorezonans napięć

W dalszym ciągu pomija się występowanie zjawiska histerezy, przyjmując że charakterystyka magnesowania dławika (cewki z rdzeniem ferromagnetycznym) jest krzywą magnesowania pierwotnego. Dławik jest elementem nieliniowym - jego charakterystyka strumień skojarzony-prąd nie jest linią prostą, co oznacza, że przy sinusoidalnie zmiennym napięciu przebieg prądu jest odkształcony i zawiera wyższe harmoniczne (rys. 1a). Zasilając dławik napięciem sinusoidalnie zmiennym o różnych wartościach skutecznych, można wyznaczyć wartość skuteczną pierwszej harmonicznej prądu w dławiku i na tej podstawie wykreślić charakterystykę prądowo-napięciową dławika U_L(I_L), przy czym jeszcze raz należy podkreślić, że U_L oraz I_L są wartościami skutecznymi pierwszych harmonicznych.

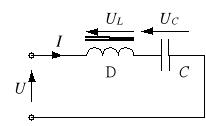
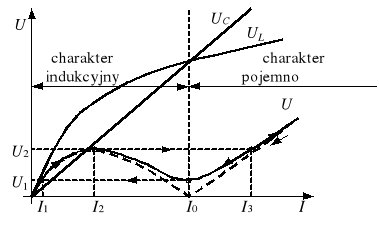
Rozważmy szeregowy układ dławik-kondensator zasilany napięciem sinusoidalnym (rys. 3a). Narysujmy charakterystyki prądowo-napięciowe dławika U_L(I) i kondensatora U_C(I) (rys. 3b) oraz charakterystykę wypadkową U(I) (linia przerywana pogrubiona), przy czym U = |U_L - U_C|, jako że poszczególne harmoniczne u_L i u_C są w przeciwfazie. Widać, że istnieje taka wartość skuteczna prądu I = I₀, dla którego wartość skuteczna napięcia zasilania U jest równa zeru (U(I₀) = 0). Jest to efekt zrównoważenia napięć U_L i U_C. Zjawisko zrównoważenia napięć na dławiku i kondensatorze poprzez dobór wartości skutecznej prądu nosi nazwę ferrorezonansu napięć. Podczas ferrorezonansu napięć równoważą się jedynie pierwsze harmoniczne napięć u_C i u_L. Ponieważ napięcia u_C i u_L zawierają wyższe harmoniczne, które nie kompensują się wzajemnie, to wartość skuteczna napięcia u_C + u_L nie spada do zera, lecz do pewnej wartości minimalnej - na rysunku 3b ferrorezonansowi napięć odpowiada punkt (I₀, U₁). Wobec tego rzeczywista charakterystyka U(I) przebiega nieco wyżej od idealnej.

a)	b)

Rys. 3. Szeregowy układ dławik-kondensator (a) oraz jego charakterystyki prądowo-napięciowe

W dalszym ciągu pomija się możliwość wystąpienia składowych podharmonicznych (drgania powolne, subharmoniczne), które dodatkowo komplikują analizę zjawiska ferrorezonansu. Gdy w układzie z rysunku 2a będziemy powoli zwiększać wartość skuteczną napięcia zasilania zaczynając od zera, to przy pewnej wartości U = U₂ nastąpi gwałtowny skok wartości skutecznej prądu I z I₂ do I₃. Powoduje to jednocześnie skok wartości skutecznych napięć na poszczególnych elementach, przy czym o ile przed skokiem wartość U_L była większa od U_C, o tyle po skoku U_L < U_C. Następuje również zmiana charakteru gałęzi z indukcyjnego na pojemnościowy. Zjawisko to nazywamy zjawiskiem przewrotu. Zauważmy, że stan ferrorezonansu (U = min) nie został przy tym osiągnięty. Dalszy wzrost wartości U powoduje ciągły wzrost wartości I. Zmniejszając następnie wartość U powodujemy ciągły spadek wartości I. Kiedy wartość U spadnie do wartości U₁, obwód znajduje się w stanie ferrorezonansu - pierwsze harmoniczne napięć na dławiku i kondensatorze są równe, a wartość skuteczna prądu w obwodzie wynosi I₀. Gdy zmniejszymy wartość U poniżej wartości U₁, nastąpi gwałtowny spadek wartości I z I₀ do I₁ z jednoczesnym skokowym spadkiem wartości skutecznych napięć na poszczególnych elementach. Dalsze zmniejszanie wartości U powoduje ciągły spadek wartości I. Zauważmy, że dla I z zakresu (I₂, I₀) nie jest możliwa stabilna praca układu (zasilanego ze źródła napięcia).

Przebieg zjawisk będzie nieco inny, gdy rozpatrywany układ zasilimy źródłem prądowym
i będziemy zwiększać lub zmniejszać wartość skuteczną prądu. W takim przypadku nie obserwuje się skoków wartości I. Zwiększanie wartości I od zera daje początkowo wzrost wartości U na zaciskach gałęzi, lecz dla wartości I większej od I₂ wartość U zaczyna maleć. Dla I = I₀ wartość U osiąga minimum (ferrorezonans). Dalsze zwiększanie wartości I powoduje ponowne zwiększanie wartości U.

Z rysunku 3b wynika, że aby zaszło zjawisko ferrorezonansu napięć, krzywe U_L(I) oraz U_C(I) muszą się przecinać. Oznacza to, że kondensator nie może mieć zbyt dużej reaktancji, gdyż wówczas przy zbyt dużym nachyleniu prostej U_C(I) nie będzie się ona przecinać z krzywą U_L(I).

2.3. Ferrorezonans prądów

Zjawisko ferrorezonansu może wystąpić również w równoległym układzie dławik-
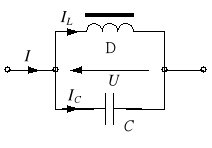
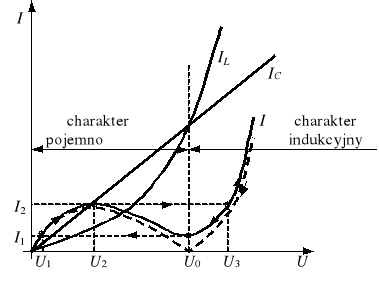
-kondensator zasilanym prądem sinusoidalnym (rys. 4a). Ferrorezonans prądów (I_L = I_C, I = min) uzyskamy poprzez zmianę wartości skutecznej napięcia U do wartości U₀ (rys. 4b). Uwagi
i uproszczenia podane przy omawianiu ferrorezonansu napięć dotyczą również ferrorezonansu prądów. W szczególności wartość skuteczna prądu I w stanie ferrorezonansu nie osiąga wartości równej zeru i rzeczywista charakterystyka I(U) przebieg nieco wyżej niż idealna.

a)	b)

Rys. 4. Równoległy układ dławik-kondensator (a) oraz jego charakterystyki prądowo-napięciowe

Gdy w układzie z rysunku 3a będziemy powoli zwiększać wartość skuteczną prądu zasilania zaczynając od zera, to przy pewnej wartości I = I₂ nastąpi gwałtowny skok wartości skutecznej napięcia U z U₂ do U₃. Powoduje to jednocześnie skok wartości skutecznej prądów poszczególnych elementów, przy czym o ile przed skokiem wartość I_L była mniejsza od I_C, o tyle po skoku I_L > I_C. Następuje również zmiana charakteru dwójnika z pojemnościowego na indukcyjny (przewrót). Stan ferrorezonansu (I = min) nie zostaje przy tym osiągnięty. Dalszy wzrost wartości I powoduje ciągły wzrost wartości U. Zmniejszając następnie wartość I powodujemy ciągły spadek wartości U. Kiedy wartość I spadnie do wartości I₁, obwód znajduje się w stanie ferrorezonansu - pierwsze harmoniczne prądów dławika i kondensatora są równe, a wartość skuteczna napięcia w obwodzie wynosi U₀. Gdy zmniejszymy wartość I poniżej wartości I₁, nastąpi gwałtowny spadek wartości U
z U₀ do U₁ z jednoczesnym skokowym spadkiem wartości skutecznych prądów poszczególnych elementów. Dalsze zmniejszanie wartości I powoduje ciągły spadek wartości U. Zauważmy, że dla U z zakresu (U₂, U₀) nie jest możliwa stabilna praca układu (zasilanego ze źródła prądu).

Przebieg zjawisk będzie nieco inny, gdy rozpatrywany układ zasilimy źródłem napięciowym
i będziemy zwiększać lub zmniejszać wartość skuteczną napięcia U. W takim przypadku nie obserwuje się skoków wartości U. Zwiększanie wartości U od zera daje początkowo wzrost wartości I, lecz dla wartości U większej od U₂ wartość I zaczyna maleć. Dla U = U₀ wartość I osiąga minimum (ferrorezonans). Dalsze zwiększanie wartości U powoduje ponowne zwiększanie wartości I.

Z rysunku 4b wynika, że aby zaszło zjawisko ferrorezonansu prądów, krzywe I_L(U) oraz I_C(U) muszą się przecinać. Oznacza to, że kondensator nie może mieć zbyt dużej reaktancji, gdyż wówczas przy zbyt małym nachyleniu prostej I_C(U) nie będzie się ona przecinać z krzywą I_L(U).

2.4. Ferrorezoansowy stabilizator napięć

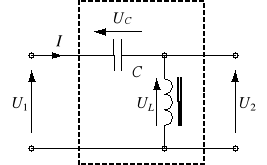
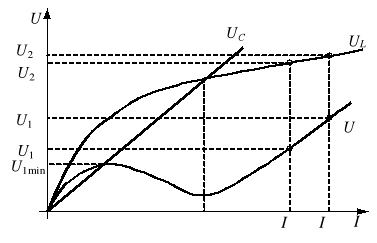
Układy ferrorezonansowe znalazły zastosowanie m.in. w stabilizacji napięć. Na rysunku 5a pokazano najprostszy układ tego rodzaju. Przypuśćmy, że na wejście układu podano napięcie U₁′. Na rysunku 5b pokazano, że odpowiada mu prąd I′ oraz napięcie na dławiku (wyjściowe) równe U₂′. Jeśli z pewnych powodów napięcie wejściowe wzrośnie do U₁″, to napięcie wyjściowe wzrośnie do wartości U₂″. Widać, że różnica U₂ = U₂″ - U₂′ jest mniejsza od U₁ = U₁″ - U₁′.

Wadą powyższego układu jest to, że pracuje on poprawnie dla napięcia zasilania większego od U_1min, a więc w stanie nasycenia rdzenia, a to jak wiadomo (rys. 1) powoduje znaczne odkształcenie krzywej prądu.

a)	b)

Rys. 5. Ferrorezonansowy stabilizator napięcia (a) i objaśnienie jego działania (b)

3. Przebieg ćwiczenia

3.1. Obserwacje przebiegów prądu i napięcia

• Zestawić układ wg rysunku 6,

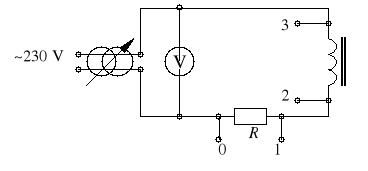
Rys. 6.

• Nastawić autotransformatorem wskazane przez prowadzącego ćwiczenia napięcie; podłączyć zaciski 0-1 do płytek odchylania pionowego oscyloskopu; zaobserwowany na ekranie przebieg przerysować; w analogiczny sposób postąpić dla zacisków 2-3 (obydwa przebiegi narysować na wspólnym wykresie),

• Pomiary powtórzyć dla dwóch innych wartości napięcia zasilania wskazanych przez prowadzącego ćwiczenia.

3.2. Badania w układzie szeregowym

• Zestawić układ wg schematu z rysunku 7 (do cewki i kondensatora podłączyć woltomierze cyfrowe; w razie braku dwóch woltomierzy zastosować jeden i podczas pomiarów przełączać woltomierz z zacisku A na B i odwrotnie),

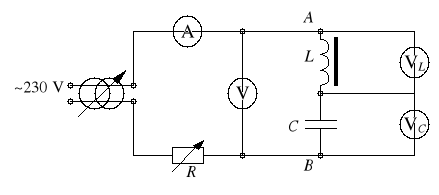
Rys. 7.

• Przed pomiarami właściwymi przeprowadzić próbę polegającą na powolnym zwiększaniu napięcia zasilania i obserwowaniu wskazań mierników; zakres amperomierza ustawić na stosunkowo duży. Zanotować napięcie U₂, dla którego następuje skok prądu oraz wartość prądu po skoku. Następnie zmniejszać powoli napięcie; zanotować napięcie U₁, dla którego następuje skok prądu. Ustawić napięcie zasilania na zero.

• Zwiększając powoli napięcie zasilania aż do wartości nieco mniejszej od U₂ notować wskazania mierników (tabela 1, wiersze oznaczone jako →),

• Przed ustawieniem napięcia U₂ zwiększyć zakres amperomierza,

• Bardzo powoli zwiększając napięcie zasilania doprowadzić do skoku prądu; dobrać zakres amperomierza i zanotować prąd oraz napięcia na cewce i kondensatorze tuż skoku,

• Zwiększając dalej napięcie zasilania wykonać jeszcze kilka pomiarów,

• Następnie zmniejszając napięcie zasilania aż do wartości nieco większej niż U₁ notować wskazania mierników (wiersze oznaczone jako ←),

• Bardzo powoli zmniejszając napięcie zasilania doprowadzić do skoku prądu; dobrać zakres amperomierza i zanotować prąd oraz napięcia na cewce i kondensatorze tuż po skoku,

• Następnie zmniejszać napięcie zasilania do zera i notować wskazania mierników.

UWAGA: W razie pomyłki podczas przeprowadzania pomiarów należy je wykonać od początku!

U, V

→

←

I, mA

→

←

UL, V

→

←

UC, V

→

←

3.3. Badania w układzie równoległym

• Zestawić układ wg schematu z rysunku 8 (amperomierze A_L i A_C są opcjonalne),

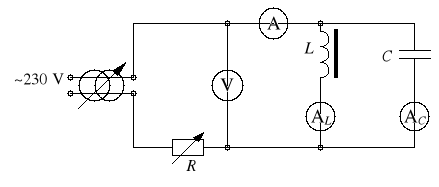
Rys. 8.

• Zwiększając stopniowo napięcie zasilania od zera do wartości nieco większej niż ferrorezonansowa, notować wskazania mierników (tabela 2); podczas pomiarów wyznaczyć maksimum i minimum prądu.

Tabela 2

U, V

I, mA

IL, mA

IC, mA

4. Opracowanie sprawozdania

1. Cel ćwiczenia.

2. Schematy pomiarowe i tabele wyników.

3. Parametry i dane znamionowe zastosowanych przyrządów.

4. Zamieścić oscylogramy zaobserwowane w punkcie 3.1.

5. Wykreślić charakterystyki prądowo-napięciowe dotyczące punktu 3.2.

6. Wykreślić charakterystyki prądowo-napięciowe dotyczące punktu 3.3; w przypadku, gdy pomiary wykonano bez amperomierzy A_L i A_C, narysować charakterystyki I_L(U) i I_C(U) na podstawie pomiarów z punktu 3.3 i obliczając |I_L - I_C|, sprawdzić, czy otrzymuje się charakterystykę zmierzoną I(U); ewentualne rozbieżności skomentować.

7. Podać przykład wykorzystania obwodu ferrorezonansowego i omówić zasadę jego działania.

8. Wnioski.

5. Pytania sprawdzające

1. Narysować przebiegi prądu, napięcia i strumienia magnetycznego w cewce z rdzeniem ferromagnetycznym przy założeniu, że napięcie jest sinusoidalnie zmienne.

2. Omówić sposób konstrukcji przebiegu prądu dla zadanego przebiegu napięcia.

3. Na czym polega ferrorezonans napięć?

4. Narysować charakterystyki prądowo-napięciowe szeregowego dwójnika dławik-kondensator.

5. Dlaczego w stanie ferrorezonansu napięć napięcie zasilania nie jest równe zeru?

6. Omówić zjawiska zachodzące w szeregowym dwójniku dławik-kondensator zasilanym ze źródła napięcia przy zwiększaniu i zmniejszaniu wartości skutecznej tego napięcia.

7. Omówić zjawiska zachodzące w szeregowym dwójniku dławik-kondensator zasilanym ze źródła prądu przy zwiększaniu i zmniejszaniu wartości skutecznej tego prądu.

8. Jak można doprowadzić do ferrorezonansu w szeregowym dwójniku dławik-kondensator zasilanym ze źródła napięcia?

9. Co to jest zjawisko przewrotu?

10. Na czym polega ferrorezonans prądów?

11. Narysować charakterystyki prądowo-napięciowe równoległego dwójnika dławik-kondensator.

12. Dlaczego w stanie ferrorezonansu prądów prąd zasilania nie jest równy zeru?

13. Omówić zjawiska zachodzące w równoległym dwójniku dławik-kondensator zasilanym ze źródła napięcia przy zwiększaniu i zmniejszaniu wartości skutecznej tego napięcia.

14. Omówić zjawiska zachodzące w szeregowym dwójniku dławik-kondensator zasilanym ze źródła prądu przy zwiększaniu i zmniejszaniu wartości skutecznej tego prądu.

15. Podać przykłady zastosowania obwodów ferrorezonansowych.

16. Omówić zasadę działania ferrorezonansowych stabilizatorów napięcia.

Literatura

[1] Bolkowski T.: Elektrotechnika teoretyczna, tom I - teoria obwodów elektrycznych, WNT,
W-wa 1986, ss. 508-516.

[2] Cholewicki T.: Elektrotechnika teoretyczna, tom II, WNT, W-wa 1970, ss. 393-399.

[3] Krakowski M.: Elektrotechnika teoretyczna, tom I - obwody liniowe i nieliniowe, PWN, W-wa 1991, ss. 614-617, 629-635.

Przebiegi prądów i napięć w obwodzie z żelazem. Ferrorezonans napięć i prądów

6

Politechnika Częstochowska, Wydział Elektryczny, Katedra Elektrotechniki

---