Politechnika Częstochowska

Wydział Elektryczny

Katedra Elektrotechniki

Zakład Elektrotechniki

Laboratorium Elektrotechniki Teoretycznej

Siatkowe modelowanie pól

Częstochowa 2004

1. Cel ćwiczenia

Celem ćwiczenia jest poznanie sposobu rozwiązywania zagadnień polowych za pomocą metody różnic skończonych i jej analogowej implementacji.

2. Wiadomości podstawowe

2.1. Pola i metody ich wyznaczana

Pole elektromagnetyczne charakteryzuje się ciągłością jego rozkładu w przestrzeni. Jednym
z problemów jest wyznaczenie tego rozkładu, tj. danie odpowiedzi na pytanie: jaka jest wartość natężenia pola (indukcji, potencjału itp.) w konkretnych punktach przestrzeni i konkretnych chwilach czasu w zadanej konfiguracji. Zadanie to sprowadza się do rozwiązania równania różniczkowego cząstkowego przy zadanych warunkach brzegowych i początkowych.

W wielu przypadkach występujących w zagadnieniach technicznych kształt obszaru działania pola jest dość złożony, a parametry materiałowe tego obszaru są różne w różnych miejscach (np. silnik elektryczny, transformator, antena itp.). Takiego problemu nie można w sposób dokładny rozwiązać metodami analitycznymi, tzn. nie można podać wzoru, do którego podstawia się współrzędne przestrzenne i czas. Wtedy stosuje się metody przybliżone. Należą do nich metody numeryczne i analogowe. Metody numeryczne polegają na sprowadzeniu zagadnienia do rozwiązania wielu równań liniowych na maszynach cyfrowych. Do metod numerycznych należą m.in. metoda różnic skończonych, metoda elementów skończonych czy metoda elementów brzegowych. Z kolei w metodach analogowych wykorzystuje się analogie pomiędzy różnymi zjawiskami fizycznymi, a ściślej - to, że dwa różne zjawiska mogą być opisane równaniem cząstkowym tego samego typu, co pozwala uzyskać informacje o obydwu zjawiskach poprzez badanie tylko jednego z nich. Do metod analogowych należą m.in. modelowanie pól statycznych na tkaninie przewodzącej, w wannie elektrolitycznej czy na modelu siatkowym.

2.2. Podstawy metody różnic skończonych dla równania Laplace'a

Metoda różnic skończonych polega na zapisaniu równania różniczkowego wraz warunkami brzegowymi i początkowymi w postaci różnicowej, tj. pochodne zastępuje się ilorazami różnicowymi. Omówimy to na przykładzie mającego duże znaczenie dwuwymiarowego równania Laplace'a

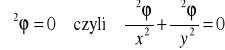
gdzie (x, y) - funkcja pola, której znaczenie fizykalne zależy od rodzaju zagadnienia, np. potencjał stałego pola elektrycznego, potencjał laminarnego pola przepływowego, potencjał stałego pola magnetycznego w obszarach bezprądowych, potencjał newtonowskiego pola grawitacyjnego
w obszarach bezmasowych, temperatura ustalona w obszarach bez źródeł ciepła.

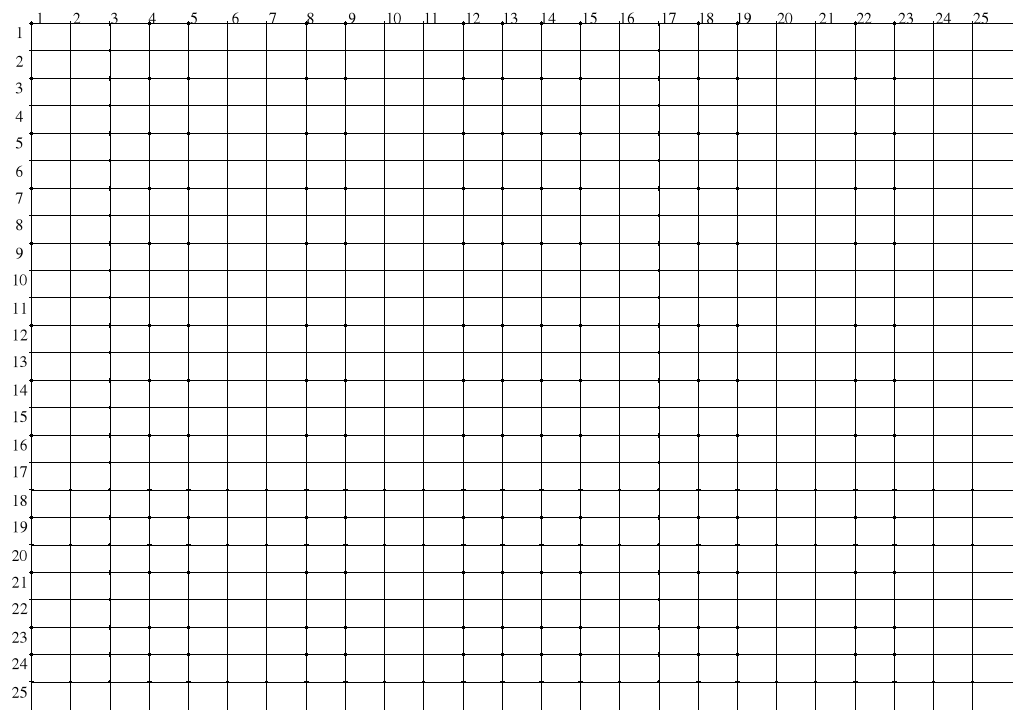
Przejście od pochodnych do ilorazów różnicowych wiąże się ze wprowadzeniem w obszarze działania pola węzłów. Zwykle rozmieszcza się je w regularnej siatce prostokątnej (rys. 1). Rozwiązanie zagadnienia polega na ułożeniu dla każdego z węzłów równania różnicowego wynikającego z postaci równania różniczkowego, a w przypadku węzłów brzegowych - dodatkowo z warunków brzegowych. Powstały układ równań rozwiązuje się ze względu na niewiadome wartości  w węzłach. Gdy w węźle zadana jest wartość funkcji , to równanie degeneruje się do trywialnej postaci  = _zadane. Równanie to można wyeliminować z układu równań, ale niekiedy nie opłaca się tego robić.

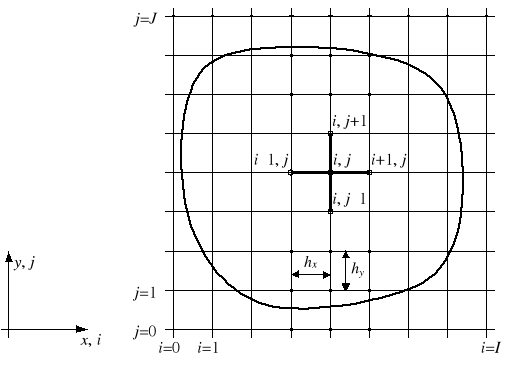
Rys. 1. Prostokątna siatka węzłów z wyróżnionym węzłem i, j i jego sąsiadami

Pochodne występujące w równaniu różniczkowym i w warunkach brzegowych zastępuje się wyrażeniami wynikającymi z szeregu Taylora, który wyraża wartość funkcji  w punkcie (x, y) poprzez wartości funkcji  i jej pochodnych w pewnym punkcie (x₀, y₀):

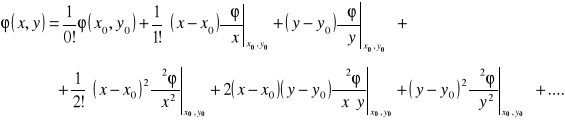
Weźmy pod uwagę dowolny węzeł (i, j). Z szeregu Taylora dla węzłów sąsiednich otrzymuje się

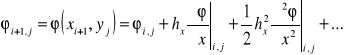
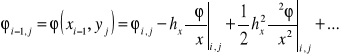
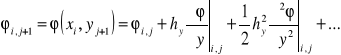
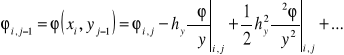
Dodając stronami pierwszą i drugą oraz trzecią i czwartą zależność, otrzymujemy odpowiednio

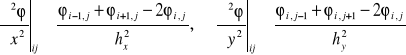
Wstawiając to do równania Lapalce'a, otrzymujemy jego różnicową postać w punkcie (i, j)

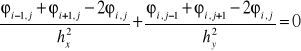
a w przypadku siatki kwadratowej (h_x = h_y)

Równania takie pisze się dla wszystkich węzłów leżących wewnątrz obszaru działania pola. Ponadto również warunki brzegowe wyraża się w postaci różnicowej. W ten sposób powstaje układ tylu równań, ile jest węzłów. Po jego rozwiązaniu znane będą wartości funkcji  w każdym
z węzłów. Jednakże otrzymane wartości węzłowe _i,j nie są na ogół równe rzeczywistym wartościom funkcji (x_i, y_j), ponieważ wyprowadzając różnicową postać równania Laplace'a
i wprowadzając warunki brzegowe pomija wyższe pochodne. Błąd rozwiązania jest tym większy, im bardziej nierównomierne jest pole, zatem dokładność wyników otrzymanych metodą różnicową nie jest w całym obszarze działania pola jednakowa. Dokładność tę można zwiększyć poprzez zastosowanie drobniejszej siatki. Można pokazać, że jeśli dwukrotnie zmniejszymy h_x i h_y, to liczba równań wzrośnie czterokrotnie, a dokładność - 16-krotnie. Z drugiej strony na rozwiązywanie układu równań na maszynie cyfrowej wnosi nowy błąd, gdyż wszystkie liczby pamiętane są tylko
z pewną dokładnością. W trakcie rozwiązywania układu równań niedokładności nakładają się na siebie. W efekcie istnieje graniczna siatka, dla której w praktyce otrzymuje się najdokładniejsze wyniki - wtedy zastosowanie drobniejszej siatki prowadzi wprawdzie do dokładniejszej aproksymacji, ale jest ona niweczona przez wzrost błędu rozwiązywania układu równań.

2.3. Metoda modelowania analogowego

Jedną z metod badania zjawisk polowych jest metoda modelowania fizycznego. Modelowanie fizyczne polega na badaniu zjawisk w modelu podobnym do rzeczywistego obiektu. Szeroko stosowane jest też modelowanie analogowe. Model ma w takim przypadku inną strukturę fizyczną niż oryginał, ale tak dobraną, że występujące w nim zjawiska są opisane równaniami o takiej samej postaci jak zjawiska w obiekcie oryginalnym.

Na modelu analogowym można w stosunkowo prosty sposób zrealizować badanie stałego pola elektrycznego lub pola prądu stałego - potencjał obydwu pól spełnia równanie Laplace'a.
W przypadku modeli ciągłych środowisko przewodzące wykonuje się z papierów lub tkanin przewodzących, a w przypadku modeli dyskretnych stosuje się siatkę rezystorów (rys. 2).

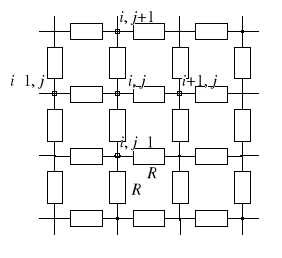
Rys. 2. Fragment siatkowy model rezystancyjnego

Rozważmy jeden węzeł takiej siatki, powiedzmy węzeł (i, j) Z metody potencjałów węzłowych wynika następujące równanie

a ponieważ wszystkie rezystory są jednakowe, to otrzymujemy

Równanie to ma identyczną strukturę jak postać różnicowa równania Laplace'a dla siatki kwadratowej. Wobec tego rozpatrywany model siatkowy opisuje to samo zjawisko, to układ równań wynikający z metody różnic skończonych. Węzły obliczeniowe w metodzie różnic skończonych odpowiadają węzłom fizycznym w modelu siatkowym, a gniazdom pomiarowym na tablicy modelu. Pomiędzy węzły można włączać nie tylko rezystory, ale również cewki czy kondensatory, co pozwala na modelowanie szerokiej gamy zjawisk. Przykładem modelowania analogowego jest też rozwiązywanie równań telegrafistów w linii długiej za pomocą łańcuchowo połączonych czwórników zawierających m.in. cewki i kondensatory. Można również modelować zjawiska opisane równaniem Poissona, ale w tym celu model siatkowy należy nieco zmodyfikować.

Szukanie rozwiązania zagadnienia brzegowego polega na zamodelowaniu równania opisującego pole, dokonaniu pomiarów wartości potencjałów V_i,j w poszczególnych węzłach modelu, a następnie przeliczeniu ich na wartości _i,j wg wzoru

gdzie k - współczynnik podobieństwa, którego wartość wynika z parametrów oryginalnego zagadnienia i z parametrów modelu siatkowego. Modelowanie równania sprowadza się do przeniesienia geometrii obszaru działania pola na tablicę pomiarową modelu siatkowego (przyjmując odpowiednie wartości h_x i h_y), a następnie na wprowadzeniu warunków brzegowych. Warunki brzegowe pierwszego rodzaju, tzn. zadane wartości brzegowe funkcji , realizuje się przez przyłożenie do odpowiednich węzłów modelu siatkowego potencjałów V odpowiadających wartościom funkcji  w tych punktach brzegowych.

Metoda modelowania siatkowego należy do przybliżonych metod rozwiązywania zagadnień brzegowych. Występujące w niej błędy wynikają przede wszystkim z dwóch powodów: po pierwsze - modeluje się nie oryginalne równanie, lecz równanie różnicowe, a po drugie - występuje problem polegający na rozrzucie parametrów modelu (np. rezystory nie mają rzeczywiście dokładnie takiej samej rezystancji, rezystancja ta zależy także od temperatury itp.). Pierwszy błąd można zmniejszyć przez dobór odpowiedniej siatki (kwadratowa, prostokątna, biegunowa), przez zagęszczenie siatki oraz przez zastosowanie różnic wyższych rzędów. To ostatnie komplikuje jednak zarówno równania, jak i sam model siatkowy.

Podsumowując, modele analogowe, a w szczególności modele siatkowe, stosuje się tam, gdzie nie jest wymagana wysoka dokładność. Zasady modelowania są dość proste, wprowadzanie warunków brzegowych oraz pomiary potencjałów w węzłach są stosunkowo dokładne i łatwe do zrealizowania. Wadą jest natomiast rozrzut parametrów modelu.

3. Przebieg ćwiczenia

3.1. Opis układu pomiarowego

W ćwiczeniu można zastosować jeden z dwóch dostępnych modeli - siatkowy oraz ciągły. Obydwa modele przeznaczone są do rozwiązywania równania dwuwymiarowego równania Laplace'a w układzie (x, y).

Model siatkowy zbudowany jest z rezystorów o wartości 10 k rozmieszczonych
w równomiernej siatce o wymiarach 25×25. Zatem siatka składa się z 625 węzłów pomiarowych. Odległość między węzłami jest stała i wynosi 2,5 cm. Model posiada wbudowany zasilacz stabilizowany, z wyprowadzonymi punktami o różnych potencjałach. Potencjały te można przenosić na tablicę pomiarową za pomocą przewodów stanowiących wyposażenie modelu. Pomiary potencjału dokonuje się woltomierzem cyfrowym.

Model ciągły wykorzystuje tkaninę przewodzącą, co pozwalają rozwiązywać bezpośrednio równanie Laplace'a, a nie jego postać dyskretną, jak ma to miejsce w modelu siatkowym. Również ten model zawiera 25×25 węzłów rozmieszczonych w kwadratowej siatce. Potencjały z zasilacza przenosi się na elektrody za pomocą przewodów, a same elektrody układa się z blach będących na wyposażeniu modelu. Pomiaru dokonuje się sondą sprzężoną z komputerem, który automatycznie zapisuje wyniki do pliku tekstowego.

3.2. Modelowanie potencjału pola elektrostatycznego

Należy wyznaczyć potencjał pola elektrostatycznego w jednej z trzech podanych niżej konfiguracji (rys. 3). W tym celu

• przyjąć h_x i h_y tak, aby konfiguracja zmieściła się na tablicy modelu, a z drugiej strony aby optymalnie wykorzystać model (skoki h_x i h_y odpowiadają odległości pomiędzy dwoma sąsiednimi węzłami modelu),

• wyznaczyć współczynnik podobieństwa k:

• za pomocą odpowiednich przewodów (lub blach w modelu ciągłym) odzwierciedlić konfigurację rzeczywistą w modelową,

• pomierzyć potencjały w węzłach leżących poza elektrodami (do notowania potencjałów można wykorzystać tabelę zamieszczoną na końcu instrukcji).

a)	b)	c)

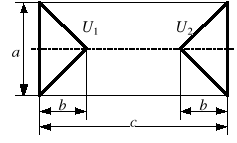
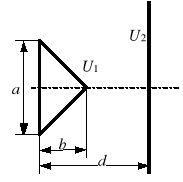
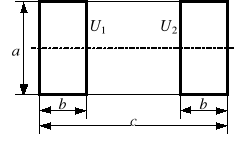
Rys. 3. Przykładowe konfiguracje: a) ostrze-ostrze, b) ostrze-płyta, c) płyta-płyta
(a = 10 cm, b = 5 cm, c = 25 cm, d = 20 cm, U₁ = 250 V, U₂ = 0 V)

3.3. Modelowanie potencjału pola przepływowego

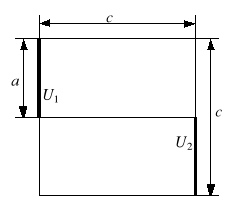
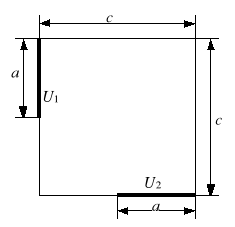
Należy wyznaczyć potencjał pola przepływowego w jednym z obszarów o stałej przewodności z rysunku 4. Pomiary przeprowadzać jak w poprzednim punkcie.

a)	b)	c)

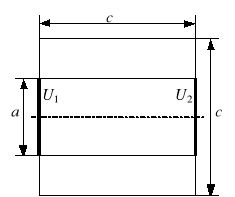
Rys. 4. Przykładowe konfiguracje: a) elektrody symetryczne, b) elektrody asymetryczne naprzeciwległe,
c) elektrody asymetryczne (a = 12 cm, c = 25 cm, U₁ = 100 V, U₂ = 0 V)

3.4. Modelowanie potencjału pola w żłobku

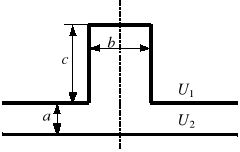
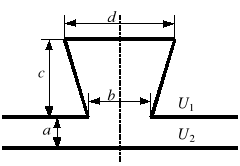
Należy wyznaczyć potencjał pola w odosobnionym żłobku stojana silnika i w szczelinie powietrznej z rysunku 5 (wybrać jedną z konfiguracji). Pomiary jak poprzednio.

a)	b)

Rys. 5. Przykładowe konfiguracje: a) żłobek prostokątny, b) żłobek trapezowy,
(a = 0,5 cm, b = 2 cm, c = 5 cm, d = 6 cm, U₁ = 100 V, U₂ = 0 V)

4. Opracowanie sprawozdania

1. Cel ćwiczenia.

2. Schematy pomiarowe i tabele wyników.

3. Parametry i dane znamionowe zastosowanych przyrządów.

4. Krótkie omówienie metody różnic skończonych i metody analogowej stosowanej w ćwiczeniu.

5. Na podstawie przeprowadzonych pomiarów nanieść linie ekwipotencjalne opisując na nich rzeczywistą, a nie modelową wartość napięcia.

6. Skomentować uzyskane wyniki.

7. Wnioski.

5. Pytania sprawdzające

1. Podać podział metod rozwiązywania zagadnień polowych i wymienić przykładowe metody.

2. Dlaczego stosuje się metody modelowania pola?

3. Omówić krótko metodę różnic skończonych.

4. Wyprowadzić postać różnicową równania Laplace'a.

5. Podać zalety i wady metody różnic skończonych.

6. Jakie błędy towarzyszą metodzie różnic skończonych.

7. Omówić krótko metodę modelowania analogowego.

8. Jakimi elementami należy uzupełnić siatkowy model rezystancyjny, aby można było na nim rozwiązywać równanie Poissona?

9. Jakie równanie rozwiązuje czwórnikowy model linii długiej?

10. Czy na modelu zastosowanym w ćwiczeniu można rozwiązywać pola trójwymiarowe?

Literatura

[1] Grzymkowski R., Kapusta A., Nowak I., Słota D.: Metody numeryczne - zagadnienia brzegowe, Wydawnictwo Pracowni Komputerowej Jacka Skalmierskiego, Gliwice 2003.

[2] Kącki E.: Równania różniczkowe cząstkowe w zagadnieniach fizyki i elektrotechniki, WNT, W-wa 1992, ss. 383-399, ss. 440-473.

[3] Krakowski M.: Elektrotechnika teoretyczna, tom II - pole elektromagnetyczne, PWN, 1991.

[4] Matusiak R.: Elektrotechnika teoretyczna, tom II - teoria pola elektromagnetycznego, WNT, W-wa 1982, ss. 163-193.

[5] Wiak S., Zwoliński G.: Wybrane problemy obliczeniowe z elektrodynamiki technicznej, Wydawnictwo Politechniki Łódzkiej, Łódź 1997.

Siatkowe modelowanie pól

8

Politechnika Częstochowska, Wydział Elektryczny, Katedra Elektrotechniki

---