Politechnika Lubelska	Laboratorium Elektrotechniki
w Lublinie	Ćwiczenie: 5a,c
Jurek Piotr Kidaj Andrzej Kwiatek Krzysztof	Semestr: IV	Grupa: ED 4.1	Rok akademicki: 1997/98
Modelowanie pól płaskich na papierze elektroprzewodzącym.		Data wykonania: 09.03.1998.	Ocena:

Wyznaczanie obrazu pola układu o symetrii cylindrycznej:

Ćwiczenie polegało na narysowaniu na wspólnym obrazie linii ekwipotencjalnych modelu prostego i odwrotnego. Przy pomocy układów jak na rysunkach. Układ był zasilany napięciem U=10V. Prąd płynący przez układ wynosił 26mA.

Parametry układu:

R=1190Ω

h=0,132mm

ρ=R⋅h=157,08Ωmm=0,157Ωm

γ=1/ρ=6,366 1/Ωm

R [mm]	U [V]	(h=0,132mm) J [A/m^2]	(h=1m) J [A/m^2]	E [V/mm]
23	7	1362	0,179	0,152
28	6	1119	0,147	0,107
36	5	871	0,114	0,069
43	4	729	0,096	0,046
54	3	581	0,076	0,027
70	2	448	0,059	0,014
88	1	356	0,047	0,006

Z przyczyn od nas niezależnych nie udało się zebrać danych dla potencjału większego niż 7 wolt.

Obliczenia:

Rezystancja przejścia: R_p=U/I=384,6Ω

Obliczamy pojemność kondensatora:

d=11mm=0,011m

a=22mm=0,022m

h=1,32⋅10^-4m

h=1,32⋅10^-4m

Sprawdzenie prawdziwości zależności: R_p⋅C=ρ⋅ε

R_p⋅C=384,6⋅3,67⋅10^-15=1,41⋅10^-12Ω

ρ⋅ε=0,157⋅8,85⋅10^-12=1,39⋅10^-12Ω

Jak widać z pomiarów, gęstość prądu maleje wraz ze wzrostem odległości od środka symetrii przewodu. Zmienia się ona hiperbolicznie podobnie jak i natężenie pola i potencjał (wykres). Można też zauważyć, że pojemność obliczona na podstawie wyników z pomiarów zgadza się z pojemnością teoretyczną zarówno dla grubości papieru przewodzącego, jak i dla kabla koncentrycznego o długości jednego metra.

Wyznaczanie obrazu pola układu o nieregularnym kształcie:

Prąd płynący w obwodzie: I=2,6mA

Obliczenia:

l₁=0,12m s₁=l₁⋅h=0,12⋅0,132⋅10^-3=1,584⋅10^-5m²

l₂=0,05m s₂=l₂⋅h=0,05⋅0,132⋅10^-3=6,6⋅10^-6m²

l₃=0,12m s₃=l₃⋅h=0,12⋅0,132⋅10^-3=1,584⋅10^-5m²

Rezystancja przejścia wyznaczona doświadczalnie:

Rezystancja przejścia obliczona analitycznie:

Jak widać, rezystancje różnią się między sobą, jest to jednak spowodowane z pewnością niedokładnością pomiarów. Duży wpływ na wynik ma wartość płynącego prądu, jednak przy tak niewielkich jego wartościach nietrudno o pomyłkę.

Modelowanie pól za pomocą programu komputerowego:

W tej części ćwiczenia dokonaliśmy pomiarów tych samych układów przy pomocy programu komputerowego QUICK FIELD. Następnie otrzymane wyniki porównaliśmy z wynikami wyznaczonymi analitycznie w poprzedniej części ćwiczenia.

Wykres potencjału i natężenia pola elektrycznego dla kabla koncentrycznego w polu elektrostatycznym:

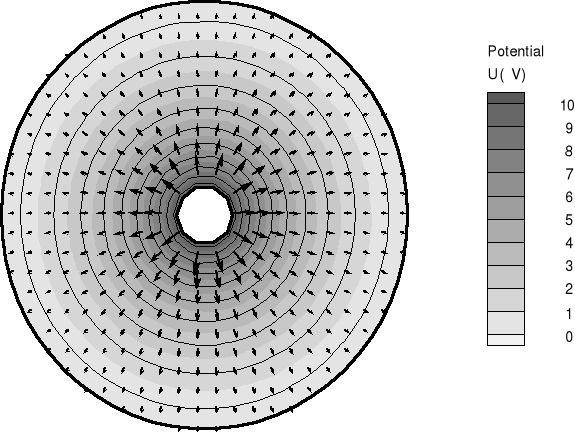
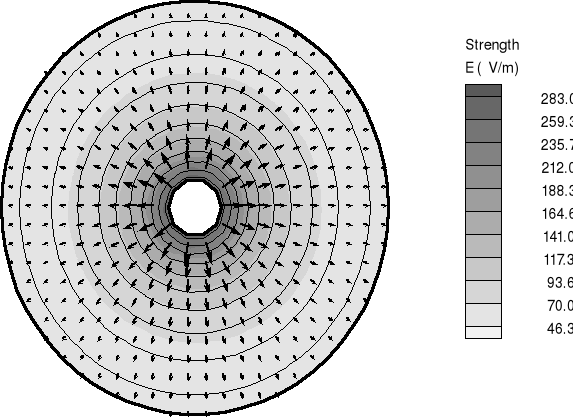
Wykres rozkładu linii ekwipotencjalnych i mapa pola elektrycznego dla walców współosiowych:

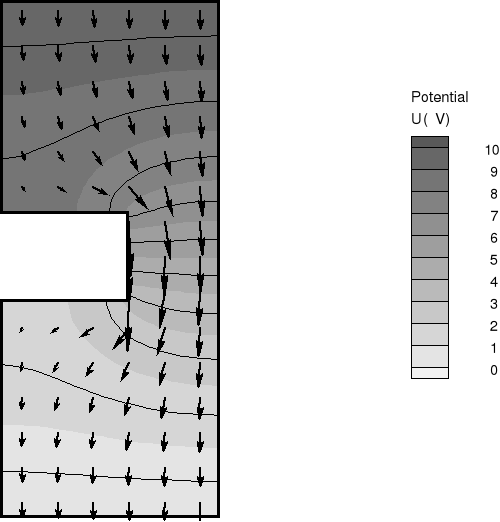
Wykres rozkładu linii ekwipotencjalnych w przewodzie wyznaczony metodą zadania odwrotnego:

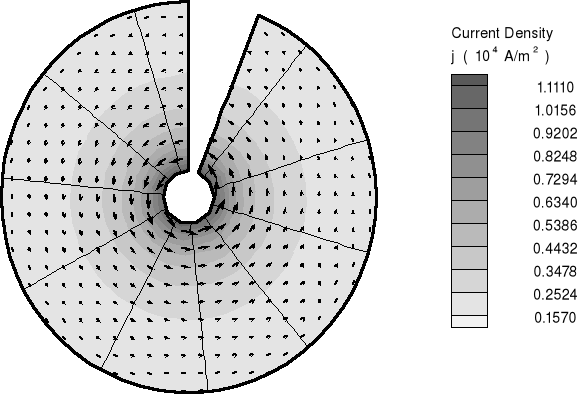
Wykres rozkładu linii ekwipotencjalnych i obraz wektorów gęstości prądu w przewodzie o zmiennym przekroju:

Potencjał V(r) i natężenie pola elektrycznego E(r) wzdłuż promienia układu walców współosiowych:

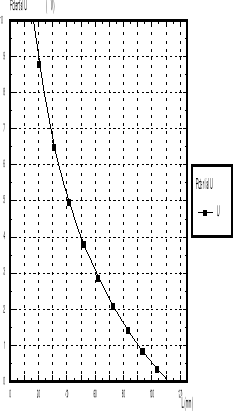
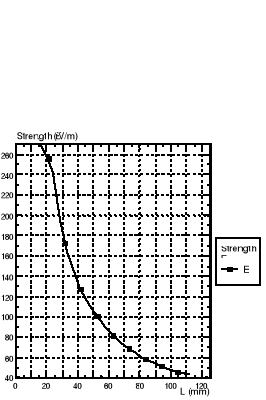
Obliczenia Przeprowadzone przy pomoc programu komputerowego:

1) Sprawdzenie prawa Gaussa:

2) Sprawdzenie pierwszego prawa Kirchhoffa:

3) Sprawdzenie drugiego prawa Kirchhoffa

Wnioski:

Na podstawie otrzymanych wyników można stwierdzić że od metody rozwiązywania równań Laplace'a znacznie prostsza jest metoda graficzna. Wymaga ona o wiele mniejszego nakładu czasu i środków: wystarcza woltomierz cyfrowy oraz papier półprzewodzący i można analizować nawet bardzo skomplikowane przypadki, których policzenie zajęłoby bardzo dużo czasu, a nawet mogłoby być niemożliwe, podczas gdy metodą graficzną wykreślenie rozkładu pola nie stanowi żadnego problemu.

Przy bardziej skomplikowanych przypadkach jednak nawet ta metoda nie jest wystarczająca. Wtedy najlepszym rozwiązaniem jest skorzystanie z programu komputerowego. Umożliwia on przygotowanie żądanego układu i po przypisaniu różnym elementom określonych parametrów, zasymulowanie jego działania.

Wyniki uzyskane przy pomocy komputera cechuje duża dokładność, możemy policzyć dowolne parametry na wybranym polu badanego układu. Zaletami tej metody są również przejrzystość i szybkość. Wadą jest natomiast sposób analizy: program dzieli badany układ na małe trójkąty, co powoduje pewną niedokładność wyników (na przykład podczas sprawdzania drugiego prawa Kirchhoffa program wskazał w obszarze 1 pewne napięcie, podczas gdy teoretycznie powinno ono być równe 0). Jednak można powiedzieć, że metoda komputerowej analizy rozkładu pola jest najlepsza.

---