Politechnika Warszawska
Wydział Inżynierii Środowiska
SPRAWOZDANIE 4
(BADANIE WŁAŚCIWOŚCI MAGNETYCZNYCH CIAŁ STAŁYCH)
Mikołaj Frankiewicz
Tomasz Madejski
Rafał Rodziewicz
Nr zespołu: 7
Grupa 5 Semestr II
R.A. 2006/07
I. CEL ĆWICZENIA
Celem laboratorium było zbadanie wpływu temperatury na właściwości magnetyczne ferromagnetyka, jak również wykreślenie pętli histerezy a także wyznaczenie temperatury Curie.
II. WPROWADZENIE
Zachowanie się ciała w zewnętrznym polu magnetycznym umożliwia klasyfikację ze względu na jego właściwości magnetyczne. Reakcją danego ciała na pole magnetyczne jest magnetyzacja, którą określamy wzorem :
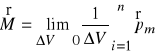
, gdzie:
pm- i-ty moment magnetyczny
V - objętość
Wzór ten należy rozumieć jako wektorową sumę momentów magnetycznych przypadających na jednostkę objętości.
W wyniku magnetyzacji ciało wytwarza własne pole w wyniku czego wypadkowy wektor indukcji B wewnątrz ciała jest równy wektorowej sumie indukcji w próżni - B0 , oraz polaryzacji magnetycznej ośrodka (μ0*M). Zależność tę możemy przedstawić wzorem:
B=B0 + μ01 ·M=
, gdzie:
μ0 - przenikalność magnetyczna próżni
μ - przenikalność magnetyczna danego ośrodka
H - natężenie zewnętrznego pola magnetycznego
χ - podatność magnetyczna
M - magnetyzacja
Ogólnie magnetyki dzielimy na:
nieuporządkowane (magnetyzm indukowany, nietrwały,dla H

0 ) które dzielimy jeszcze na: diamagnetyki(antyrównoległe wektory M i H) i paramagnetyki (równoległe wektory M i H)uporządkowane (magnetyzm spontaniczny, trawały, również dla H = 0) które dzielą się jeszcze na: ferromagnetyki, antyferromagnetyki, ferrimagnetyki i struktury niekolinearne.
Aby zrozumieć przebieg naszego doświadczenia musimy wiedzieć jeszcze, że podatność magnetyczną paramagnetyków w zależności od temperatury określa wzór Curie-Weissa:
, gdzie:
C - stała Curie
T - temperatura
Θ - paramagnetyczna temperatura Curie
W naszym doświadczeniu mieliśmy do czynienia z próbką ferromagnetyka, który min. tym wyróżnia się z pośród pozostałych magnetyków, że wewnętrzne pole magnetyczne może przewyższać, setki, tysiące, a w przypadku specjalnych stopów nawet miliony razy wywołujące je zewnętrzne pole magnetyczne.
Tak więc ferromagnetyki charakteryzują się bardzo dużą wartością podatności magnetycznej zależną od zewnętrznego pola magnetycznego oraz od temperatury otoczenia. Ferromagnetyki osiągają często stan nasycenia namagnesowania pod wpływem zewnętrznego pola magnetycznego o bardzo małym natężeniu (rzędu 10 A/m). Po usunięciu zewnętrznego pola ferromagnetyki zachowują stan namagnesowania zwany pozostałością magnetyczną. Ferromagnetyki swe osobliwe właściwości magnetyczne tracą w pewnej temperaturze (TC) nazywanej punktem ferromagnetycznym Curie. W temperaturze tej ferromagnetyzm ( czyli spontaniczne ustawienie zgodnych kierunków i zwrotów momentów magnetycznych pod wpływem czynnika porządkującego) zostaje zniszczony przez wzbudzenia termiczne i w wyższych temperaturach ferromagnetyki zachowują się jak paramagnetyki. Jednak w obszarze ferromagnetycznego punktu Curie krzywe doświadczalne podatności magnetycznej przebiegają powyżej linii prostej określonej prawem Curie-Weissa.
Dzięki nowoczesnej technologii nie musieliśmy obliczać napięcia z wzoru:
![]()
robił to za nas komputer według powyższego wzoru, w którym:
Z - ilości zwojów, S - powierzchni przekroju cewki, ![]()
- szybkość zmian pola magnetycznego.
III. WYKONANIE ĆWICZENIA
Rozpoczynamy grzanie ferromagnetyka i zapisujemy punkty pomiarowe, zwiększając co pewien okres czasu moc grzałki, w celu zachowania stałego wzrostu temperatury. W momencie zaobserwowania gwałtownego spadku napięcia rejestrowanego zwiększamy gęstość zapisu punktów.
Temperaturę danego ferromagnetyka zwiększamy dzięki mocy grzałki i zapisujemy wyniki napięcia dla danej temperatury. W chwili momentalnego spadku napięcia zmniejszamy odstęp pomiędzy kolejnymi wynikami.
IV. TABELE Z WYNIKAMI I WYKRESY
Tabela z pomiarami:
Temperatura [°C] |
U [mV] |
||||
23 |
± |
0,69 |
0,631 |
± |
0,0095 |
29 |
± |
0,87 |
0,626 |
± |
0,0094 |
32 |
± |
0,96 |
0,625 |
± |
0,0094 |
40 |
± |
1,20 |
0,622 |
± |
0,0093 |
45 |
± |
1,35 |
0,621 |
± |
0,0093 |
50 |
± |
1,50 |
0,620 |
± |
0,0093 |
55 |
± |
1,65 |
0,618 |
± |
0,0093 |
60 |
± |
1,80 |
0,614 |
± |
0,0092 |
65 |
± |
1,95 |
0,614 |
± |
0,0092 |
70 |
± |
2,10 |
0,610 |
± |
0,0092 |
75 |
± |
2,25 |
0,607 |
± |
0,0091 |
80 |
± |
2,40 |
0,602 |
± |
0,0090 |
85 |
± |
2,55 |
0,601 |
± |
0,0090 |
90 |
± |
2,70 |
0,597 |
± |
0,0090 |
95 |
± |
2,85 |
0,592 |
± |
0,0089 |
100 |
± |
3,00 |
0,588 |
± |
0,0088 |
105 |
± |
3,15 |
0,583 |
± |
0,0087 |
110 |
± |
3,30 |
0,576 |
± |
0,0086 |
115 |
± |
3,45 |
0,571 |
± |
0,0086 |
120 |
± |
3,60 |
0,562 |
± |
0,0084 |
125 |
± |
3,75 |
0,552 |
± |
0,0083 |
130 |
± |
3,90 |
0,542 |
± |
0,0081 |
135 |
± |
4,05 |
0,530 |
± |
0,0080 |
140 |
± |
4,20 |
0,517 |
± |
0,0078 |
145 |
± |
4,35 |
0,504 |
± |
0,0076 |
150 |
± |
4,50 |
0,488 |
± |
0,0073 |
155 |
± |
4,65 |
0,475 |
± |
0,0071 |
160 |
± |
4,80 |
0,456 |
± |
0,0068 |
165 |
± |
4,95 |
0,438 |
± |
0,0066 |
170 |
± |
5,10 |
0,412 |
± |
0,0062 |
175 |
± |
5,25 |
0,374 |
± |
0,0056 |
180 |
± |
5,40 |
0,315 |
± |
0,0047 |
185 |
± |
5,55 |
0,237 |
± |
0,0036 |
185 |
± |
5,55 |
0,236 |
± |
0,0035 |
186 |
± |
5,58 |
0,222 |
± |
0,0033 |
187 |
± |
5,61 |
0,212 |
± |
0,0032 |
187 |
± |
5,61 |
0,200 |
± |
0,0030 |
188 |
± |
5,64 |
0,193 |
± |
0,0029 |
189 |
± |
5,67 |
0,183 |
± |
0,0027 |
189 |
± |
5,67 |
0,172 |
± |
0,0026 |
190 |
± |
5,70 |
0,166 |
± |
0,0025 |
190 |
± |
5,70 |
0,155 |
± |
0,0023 |
191 |
± |
5,73 |
0,148 |
± |
0,0022 |
192 |
± |
5,76 |
0,137 |
± |
0,0021 |
193 |
± |
5,79 |
0,125 |
± |
0,0019 |
194 |
± |
5,82 |
0,117 |
± |
0,0018 |
195 |
± |
5,85 |
0,113 |
± |
0,0017 |
196 |
± |
5,88 |
0,100 |
± |
0,0015 |
197 |
± |
5,91 |
0,095 |
± |
0,0014 |
198 |
± |
5,94 |
0,092 |
± |
0,0014 |
199 |
± |
5,97 |
0,084 |
± |
0,0013 |
200 |
± |
6,00 |
0,079 |
± |
0,0012 |
201 |
± |
6,03 |
0,072 |
± |
0,0011 |
202 |
± |
6,06 |
0,069 |
± |
0,0010 |
202 |
± |
6,06 |
0,066 |
± |
0,0010 |
203 |
± |
6,09 |
0,063 |
± |
0,0009 |
204 |
± |
6,12 |
0,057 |
± |
0,0009 |
205 |
± |
6,15 |
0,054 |
± |
0,0008 |
206 |
± |
6,18 |
0,049 |
± |
0,0007 |
207 |
± |
6,21 |
0,047 |
± |
0,0007 |
208 |
± |
6,24 |
0,044 |
± |
0,0007 |
209 |
± |
6,27 |
0,042 |
± |
0,0006 |
210 |
± |
6,30 |
0,041 |
± |
0,0006 |
211 |
± |
6,33 |
0,039 |
± |
0,0006 |
212 |
± |
6,36 |
0,037 |
± |
0,0006 |
213 |
± |
6,39 |
0,036 |
± |
0,0005 |
214 |
± |
6,42 |
0,035 |
± |
0,0005 |
215 |
± |
6,45 |
0,034 |
± |
0,0005 |
216 |
± |
6,48 |
0,033 |
± |
0,0005 |
217 |
± |
6,51 |
0,032 |
± |
0,0005 |
218 |
± |
6,54 |
0,031 |
± |
0,0005 |
219 |
± |
6,57 |
0,029 |
± |
0,0004 |
220 |
± |
6,60 |
0,03 |
± |
0,0005 |
222 |
± |
6,66 |
0,029 |
± |
0,0004 |
223 |
± |
6,69 |
0,029 |
± |
0,0004 |
224 |
± |
6,72 |
0,028 |
± |
0,0004 |
225 |
± |
6,75 |
0,028 |
± |
0,0004 |
226 |
± |
6,78 |
0,027 |
± |
0,0004 |
Wykres spadku napięcia od temperatury:
Kwadraty błędu są bardzo małe, tak, więc często pokrywają się z punktami lub zlewają się.
Tabela z pomiarami, gdzie zauważono większy spadek napięcia:
Wyznaczanie temperatury Curie |
||||||||
Temperatura [°C] |
U [mV] |
1/U [1/mV] |
||||||
175 |
± |
5,25 |
0,374 |
± |
0,0056 |
2,674 |
± |
0,0401 |
180 |
± |
5,40 |
0,315 |
± |
0,0047 |
3,175 |
± |
0,0476 |
185 |
± |
5,55 |
0,237 |
± |
0,0036 |
4,219 |
± |
0,0633 |
185 |
± |
5,55 |
0,236 |
± |
0,0035 |
4,237 |
± |
0,0636 |
186 |
± |
5,58 |
0,222 |
± |
0,0033 |
4,505 |
± |
0,0676 |
187 |
± |
5,61 |
0,212 |
± |
0,0032 |
4,717 |
± |
0,0708 |
187 |
± |
5,61 |
0,200 |
± |
0,0030 |
5,000 |
± |
0,0750 |
188 |
± |
5,64 |
0,193 |
± |
0,0029 |
5,181 |
± |
0,0777 |
189 |
± |
5,67 |
0,183 |
± |
0,0027 |
5,464 |
± |
0,0820 |
189 |
± |
5,67 |
0,172 |
± |
0,0026 |
5,814 |
± |
0,0872 |
190 |
± |
5,70 |
0,166 |
± |
0,0025 |
6,024 |
± |
0,0904 |
190 |
± |
5,70 |
0,155 |
± |
0,0023 |
6,452 |
± |
0,0968 |
191 |
± |
5,73 |
0,148 |
± |
0,0022 |
6,757 |
± |
0,1014 |
192 |
± |
5,76 |
0,137 |
± |
0,0021 |
7,299 |
± |
0,1095 |
193 |
± |
5,79 |
0,125 |
± |
0,0019 |
8,000 |
± |
0,1200 |
194 |
± |
5,82 |
0,117 |
± |
0,0018 |
8,547 |
± |
0,1282 |
195 |
± |
5,85 |
0,113 |
± |
0,0017 |
8,850 |
± |
0,1327 |
196 |
± |
5,88 |
0,100 |
± |
0,0015 |
10,000 |
± |
0,1500 |
197 |
± |
5,91 |
0,095 |
± |
0,0014 |
10,526 |
± |
0,1579 |
198 |
± |
5,94 |
0,092 |
± |
0,0014 |
10,870 |
± |
0,1630 |
199 |
± |
5,97 |
0,084 |
± |
0,0013 |
11,905 |
± |
0,1786 |
200 |
± |
6,00 |
0,079 |
± |
0,0012 |
12,658 |
± |
0,1899 |
201 |
± |
6,03 |
0,072 |
± |
0,0011 |
13,889 |
± |
0,2083 |
202 |
± |
6,06 |
0,069 |
± |
0,0010 |
14,493 |
± |
0,2174 |
202 |
± |
6,06 |
0,066 |
± |
0,0010 |
15,152 |
± |
0,2273 |
203 |
± |
6,09 |
0,063 |
± |
0,0009 |
15,873 |
± |
0,2381 |
204 |
± |
6,12 |
0,057 |
± |
0,0009 |
17,544 |
± |
0,2632 |
205 |
± |
6,15 |
0,054 |
± |
0,0008 |
18,519 |
± |
0,2778 |
Wykres, z którego odczytujemy wartość temperatury Curie( w °C ):
Kwadraty błędu są bardzo małe, tak, więc często pokrywają się z punktami lub zlewają się.
Z wykresu jesteśmy wstanie stwierdzić, że temperatura Curie wynosi ok. 178 °C
![]()
.
V. Wnioski
Wyznaczona przez nas temperatura Curie wynosi![]()
, po osiągnięciu tej temperatury ferromagnetyk traci swoje właściwości ferromagnetyka i zachowuje się jak paramagnetyk. Jest to spowodowane wzrostem miary nieuporządkowania.
Wymiar różni się od prawdziwej wartości Tc z powodu niedokładności sprzętu, jak i błędu wynikającego z odczytania wyniku z wykresu.
- 6 -
Wyszukiwarka
Podobne podstrony:
Cwiczenie 1 lab fiz, PW Transport, Gadżety i pomoce PW CD2, płytki, ChujWieCo, fizyka, fizyka, spraw
do sprawka, PW Transport, Gadżety i pomoce PW CD2, płytki, ChujWieCo, fizyka, fizyka, Curie
Badanie odbicia światła od powierzchni dielektryków, PW Transport, Gadżety i pomoce PW CD2, płytki,
sprawo 24, PW Transport, Gadżety i pomoce PW CD2, płytki, ChujWieCo, fizyka, fizyka, od Marka, Fizyk
POLITECHNIKA WARSZAWSKA, PW Transport, Gadżety i pomoce PW CD2, płytki, ChujWieCo, fizyka, fizyka
01 Śrubka, PW Transport, Gadżety i pomoce PW CD2, płytki, ChujWieCo, fizyka, fizyka, od Marka, Fizyk
dobre30.1, PW Transport, Gadżety i pomoce PW CD2, płytki, ChujWieCo, fizyka, fizyka, od Marka, Fizyk
ferromagnetyki, PW Transport, Gadżety i pomoce PW CD2, płytki, ChujWieCo, fizyka, fizyka, od Marka,
cw. 1mm, PW Transport, Gadżety i pomoce PW CD2, płytki, ChujWieCo, fizyka, fizyka, sprawozdanie 1
więcej podobnych podstron