WYKŁAD 1

Przewidywanie - orzekanie o zdarzeniach nieznanych na podstawie zdarzeń znanych.

Wyniki przewidywania są niepewne ale przewidujemy wychodząc z założenie że lepiej jest wiedzieć o przyszłości coś niż nie wiedzieć nic.

Te zdarzenia nieznane, o których formułujemy sądy, mogą pochodzić z przeszłości (np. oceniamy zasobność złóż miedzi) lub z przyszłości (np. przewidywanie sprzedaży).

Przewidywanie nieracjonalne - wróżki, jasnowidze itp. - tym się nie będziemy zajmować.

Zdroworozsądkowe - na podstawie swojego doświadczenia (Góral może na podstawie własnego doświadczenia spróbować przewidzieć pogodę w Tatrach).

Naukowe - występuje logiczny związek między przesłankami a sformułowaną konkluzją (wnioskiem).

Przesłanki - pewne fakty i ich interpretacje.

Prognoza - sąd spełniający 4 warunki:

• jest sformułowany z wykorzystaniem dorobku nauki - np. sondaże przedwyborcze, które dostarczają materiału do naukowych badań statystycznych; prawa popytu i podaży, które pozwalają nam stwierdzić co się stanie gdy podniesiona zostanie wysokość akcyzy na samochody;

• odnoszący się do określonej przyszłości - należy sprecyzować okres bądź moment w którym przewidywane zdarzenie nastąpi;

• weryfikowalny empirycznie,

• niepewny ale akceptowany.

Funkcje prognoz:

• preparacyjna - budowa prognozy jest działaniem przygotowującym inne działania, stanowi podstawę podjęcia innych działań (np. aby podjąć działalność produkcyjną należy zbadać, czy będzie popyt na ten produkt; jeśli dyrektor muzeum chce sprowadzić za duże pieniądze obrazy Picassa, musi zbadać, czy ludzie będą chcieli je oglądać);

• aktywizująca - zachęca do podejmowania działań sprzyjających realizacji prognozy jeżeli prognoza zapowiada nastąpienie zdarzeń korzystnych bądź zachęca do podejmowania działań zapobiegających realizacji prognozy gdy prognoza zapowiada nadejście zdarzeń niekorzystnych (prognozy ostrzegawcze);

• informacyjna - ma za zadanie oswoić nas ze zmianami nadchodzącymi.

Rodzaje prognoz:

1. Ze względu na charakter zmiennych prognozowanych (zmienna - sposób wyrażenia zjawiska):

1. jakościowe

2. ilościowe

• punktowe (np. z pewnym prawdopodobieństwem produkcja piwa wyniesie w danym roku dokładnie 50 tys. hektolitrów)

• przedziałowe (np. z pewnym prawdopodobieństwem produkcja piwa w danym roku będzie się zawierała w przedziale 48 - 52 tys. hektolitrów).

2. Ze względu na typ zmian prognozowanej zmiennej:

Zmiany jakościowe - któryś z czynników zmieni swoje oddziaływanie lub pojawi się nowy czynnik, inaczej mówiąc zmienia się dotychczasowa prawidłowość bądź zmieniają się związki między badanymi zjawiskami

Zmiany ilościowe - jeżeli zmiany w przyszłości będą następowały zgodnie z dotychczasową tendencją (prawidłowością), tzn. kiedy w przyszłości na zjawisko będą oddziaływały te same czynniki co w przeszłości i oddziaływanie to będzie podobne.

1. krótkookresowe - tylko zmiany ilościowe,

2. średniookresowe - dominują zmiany ilościowe ale pojawiają się również jakościowe,

3. długookresowe - w dużym stopniu dominują zmiany jakościowe.

NIE CZAS jest tu kryterium podziału, gdyż duże znaczenie ma tu wielkość obiektu, np. gdybyśmy robili prognozy liczbę ludności Polski na 5 lat to zmiany będą stabilne (prognoza krótkookresowa); natomiast prognoza krótkookresowa dla przedsiębiorstwa może być na miesiąc, może kwartał...).

Etapy prognozowania

1. Sformułowanie zadania prognostycznego - jest to określenie:

• obiektu, zjawiska, zmiennej

• horyzontu prognozy

• celu wyznaczania prognozy

• wymagań co do jakości prognozy.

2. Podanie przesłanek prognostycznych:

• sformułowanie hipotez o czynnikach kształtujących zjawisko

• deklaracja postawy wobec przyszłości zjawiska

Postawa pasywna - przyszłość jest nieuniknionym następstwem przeszłości, określonym przez konieczne i niezależne od ludzi związki między zjawiskami. Związki te są trwałe - zjawiska kształtuje duże inercja. Prognosta musi odgadnąć „prawo ruchu”.

Postawa aktywna - przyszłość jest stosunkowo niezależna od przeszłości. Wpływają na nią pragnienia i dążenia ludzi. Ludzie kreując nowe potrzeby naruszają dotychczasowe związki między zjawiskami. Prognoza szuka faktów „niosących przyszłość”, antycypuje ludzkie potrzeby i działania.

• określenie zbioru danych potrzebnych do sporządzenia prognozy

• zebranie danych

3. Wybór metody prognozowania

Metoda prognozowania składa się z dwóch etapów:

• przetworzenie danych o przeszłości,

• przejście od danych o przeszłości do przyszłości; reguły przejścia do przyszłości:

Reguła podstawowa - prognozą jest stan zmiennej otrzymanej z modelu przy założeniu, że model będzie aktualny w przyszłości; stosujemy przy prognozowaniu zjawisk obdarzonych dużą inercją.

Przy klasycznym modelu regresji liniowej jest to reguła prognozy nieobciążonej, wg której:

t > n

Reguła podstawowa z poprawką:

Reguła największego prawdopodobieństwa

Reguła minimalnej straty

Podstawowe grupy metod prognozowania:

1. metody analizy i prognozowania szeregów czasowych

2. metody prognozowania przyczynowo-skutkowego

3. metody analogowe

4. metody prognostyczne

4. Wyznaczenie prognozy -otrzymanie pewnej wielkości y*, którą nazywamy prognozą

5. Ocena dopuszczalności prognozy - sprawdzenie wymagań prognozy co do jakości.

Błąd ex-ante - oczekiwany, spodziewany rząd odchyleń naszej prognozy od wartości, która wystąpi:

• bezwzględny V_t - wielkość mianowana (np. 100 ton)

• względny η_t - określany w procentach

Dopuszczalność prognoz - prognozą dopuszczalną jest sąd spełniający co najmniej jeden z poniższych warunków:

1. 
   którego błąd ex-ante jest co najwyżej równy z góry zadanemu:

są to wartości z góry zadane

2. 
   którego prawdopodobieństwo spełnienia się jest co najmniej równe z góry zadanemu:

to prawdopodobieństwo z góry zadane

3. dla którego błędy ex-post prognoz wygasłych nie przekraczały wartości z góry zadanych;

Prognoza wygasła - budowana na okres, który już minął, gdy znamy wartość rzeczywistą.

Trafność prognoz:

• 
  bezwzględny błąd ex-post

• 
  względny błąd ex-post

4. który został oceniony jako godny zaufania przez niezależnych ekspertów

5. który został oceniony jako godny zaufania przez twórcę prognozy

6. Weryfikacja prognozy

WYKŁAD 2

Szereg czasowy - chronologicznie uporządkowany ciąg obserwacji dotyczących badanego zjawiska zaobserwowanych w kolejnych momentach (okresach).

y = [y₁, y₂, ...., y_n] t = 1, ..., n

Muszą być kolejne, np. roczne - to nie mogą być: rok 1981, 82, a później 85 tylko wszystkie.

Często ma miejsce sytuacja, że jedynym źródłem informacji o prognozowanym zjawisku jest właśnie szereg czasowy, a nie ma informacji o czynnikach, które wpływają na to zjawisko. Ważna jest identyfikacja składowych szeregu czasowego. Składowe szeregów czasowych:

Na każde zjawisko oddziaływają przyczyny główne i uboczne.

Główne - oddziaływają zawsze, z mniej więcej tą samą siłą i tym samym kierunku. Efektem ich oddziaływania jest prawidłowość, która występuje w zjawisku. Tą prawidłowość przedstawia właśnie składowa systematyczna.

Uboczne - powodują odchylenia od prawidłowości, działają na zjawisko w różnym czasie, z różną siłą, składnik losowy w modelu ekonometrycznym (składowa przypadkowa).

Przyjmujemy, że w długim ciągu obserwacji odchylenia w jedną i drugą stronę wzajemnie się niwelują.

Szukamy więc składowej systematycznej.

Stały poziom składowej systematyczne - zjawisko przyjmuje mniej więcej te same wartości przez n momentów.

Tendencja rozwojowa - zjawisko wykazuje jednokierunkowe skłonności zmiany (rośnie lub maleje)

Wahania okresowe - są efektem działania czynników pojawiających się co pewien czas, np. sinusoida:

Wahania sezonowe - przedział nie dłuższy niż rok, związane głównie ze zmianami kalendarze i związanymi z tym naszymi zachowaniami.

Wahania cykliczne - dłuższe niż rok, np. koniunkturalne, cykle gospodarcze (ożywienie, rozkwit, recesja, depresja).

Wahania okresowe nigdy nie występują samoistnie - zawsze nakładają się bądź na stały poziom bądź na tendencję rozwojową.

Jeżeli zjawisko ma dostatecznie długą historię, to zawsze informacje w postaci szeregu czasowego znajdziemy, nie zawsze jednak na jego podstawie będzie można prognozować.

O zmienności danego zjawiska mówi nam współczynnik zmienności:

Jeżeli wynosi on np. 60% to znaczy, że udział składowej przypadkowej jest bardzo duży. Takie szeregi podstawą do prognozowania nie mogą być.

Do identyfikacji szeregu posługujemy się zwykle wykresem szeregu czasowego, musimy jednak uważać przy dobieraniu skali osi rzędnych.

Stały poziom składowej systematycznej

Mamy dwie metody prognozowania:

• metodę średniej ruchomej

• metodę prostego wygładzania wykładniczego.

1. Metoda średniej ruchomej

Mamy szereg czasowy liczący n elementów to prognozą na okres t jest średnia z k kolejnych elementów:

t	yt	y*(3)	y*(4)
1	y1
2	y2
3	y3
4	y4	y*4
5	y5	y*5	y*5
6	y6	Y*6	Y*6
7	y7	y*7	Y*7
8	y8	y*8	Y*8

Problem polega na tym, ile ostatnich okresów należy przyjąć. Zależy to w dużym stopniu od długości szeregu czasowego. Jeżeli szeregi nie są zbyt długie to k waha się w przedziale od 3 do 7, dla długich wynosi kilkadziesiąt. Jeżeli jednak stajemy przed problemem czy k = 3 czy też k = 4 to należy zbudować prognozy wygasłe (patrz tabela y*₍₃₎ i y*₍₄₎ ). Tak więc y*₄ to średnia y₁, y₂ i y₃ itd. Sprawdzamy następnie błąd prognozy, a więc y₄ - y*₄. Oczywiście chcemy aby te odchylenia były jak najmniejsze. Posłużymy się jednym z możliwych błędów ex-post:

• pierwiastkiem średniokwadratowego błędu prognoz:

i oczywiście wybieramy to k, dla którego S^* jest najmniejsze.

• średnią ruchomą ważoną

Ważniejsze są obserwacje z przeszłości „nowsze”, bliższe w czasie, z bliższych okresów. Możemy więc nadać im wagi ważności, zróżnicowane co do oddalenia w czasie - najnowsza ma być „najwięcej warta”, a więc powinna mieć największą wagę. Liczymy więc średnią ruchomą ważoną:

2. Metoda prostego wygładzania wykładniczego

Model ten wygląda następująco:

α - stała wygładzania z przedziału (0;1), prognosta wybiera ją sam.

y_t-1 - poprzednia obserwacja, ją znamy

y*_t-1 - prognoza tej poprzedniej obserwacji;

Tu znów możemy się posłużyć prognozami wygasłymi i porównać błędy, np. średniokwadratowe:

i testując różne α wybrać taką, która w przeszłości dawała najlepsze dopasowanie i przy wykorzystaniu tej α zbudować prognozę. Pojawia się pytanie - skąd wziąć poprzednią prognozę.

Posłużmy się modelem:

Tak więc pierwsza prognoza to po prostu pierwsza obserwacja.

Można też inaczej wyznaczyć α, która (w drugim zapisie) stoi przy q_t-1, czyli błędzie poprzedniej prognozy. Jeżeli chcemy ten błąd uwzględnić w dużym stopniu to trzeba tą α wziąć dużą, jeśli w małym to małą.

Tendencja rozwojowa

W szeregu czasowym występuje trend. Najprostszy przypadek - trend da się opisać funkcją liniową. Można więc trend wyrażać za pomocą funkcji, można też wyrażać za pomocą tzw. metod mechanicznych czyli szukając kolejnych wartości, które by ten trend dobrze wyrażały.

W modelu analitycznym takie funkcje jak: liniowa, potęgowa, wykładnicza, hiperbola, wielomiany (uważać na wysokie stopnie wielomianów), funkcja logarytmiczna i logistyczna. Można funkcje nieliniowe transformować do funkcji liniowej (oprócz logistycznej).

Funkcja liniowa: y_t = at + b. Parametry a i b szacuje się MNK.

Parametr a jest współczynnikiem kierunkowym - tangens kąta nachylenia, mówi jak zmienia się zjawisko w czasie (rośnie czy maleje).

Chcemy aby funkcja trendu rzeczywiście opisywała zjawisko. O trendzie mówimy wówczas gdy zmiany będą istotne. Trzeba więc zweryfikować hipotezę o istotności współczynnika kierunkowego.

Macierz wariancji i kowariancji ocen parametrów:

Musimy odpowiedzieć na pytanie czy parametry są równe czy różne od zera:

Mamy statystykę empiryczną, którą należy porównać z teoretyczną na pewnym poziomie istotności.

Możemy również policzyć współczynnik korelacji między zmienną czasową a zmienną prognozowaną. Jeżeli będzie np. tendencja wzrostowa to współczynnik korelacji będzie dodatni znaczny (istotny).

W modelu, który ma opisywać trend ważne jest aby R (współczynnik determinacji) był bliższy 1 (model bardziej dopasowany).

Jeżeli oszacujemy model, który spełni wyżej opisane kryteria i będziemy budować model na jakiś okres T to wyznaczenie prognozy jest sprawą prostą:

Gdzie w miejsce t wstawiamy numer interesującego nas okresu.

Mówi się, że w ten sposób wyznaczana prognoza jest wyznaczana drogą ekstrapolacji, czyli to równanie wyraża prawidłowości zmian w pewnym okresie czasu. Oznacza to, że prawidłowość z przeszłości przenosimy w przyszłość. Tak można wyznaczyć prognozę gdy postawa prognosty jest postawą pasywną.

Jeżeli taką prognozę wyznaczymy to należy wyznaczyć dopuszczalność tej prognozy - służą tu błędy ex ante. Dla liniowego modelu są to błędy:

Bezwzględny:

Względny:

S - standardowy błąd oceny modelu (pierwiastek z wariancji)

Prognoza punktowa:

Prognoza przedziałowa

• (bezpieczniejszą)

• dolną i górną granicę przedziału, w którym z pewnym prawdopodobieństwem będzie zawarta przyszła wielkość prognozowanego zjawiska:

Gdzie:

u - współczynnik związany z wiarygodnością modelu, rozkładem reszt modelu oraz długością szeregu czasowego

V_T - bezwzględny błąd ex ante prognozy

p - wiarygodność prognozy (np. 0,95)

Jeżeli nic nie wiemy o rozkładzie reszt modelu to wielkość współczynnika u znajdujemy korzystając z nierówności Czebyszewa:

Jeżeli możemy stwierdzić, że rozkład reszt modeli jest rozkładem normalnym to współczynnik u odczytujemy z tablic - przy małej próbie z tablic rozkładu Studenta (n-2 stopni swobody i p-stwa

1 - p), przy dużej - rozkładu normalnego

Lepsza oczywiście jest sytuacja gdy rozkład jest normalny bo wtedy wielkość współczynnika u jest mniejsza.

Prognoza z poprawką

• pojawia się sytuacja, że należy spodziewać się pewnych zmian jakościowych zjawiska - w

n-tym okresie wystąpiła obserwacja, która znajduje się z dala od linii (y_n).

Można też wygładzać szereg w sposób mechaniczny, budować prognozy adaptacyjne.

Przykładową metodą jest liniowy model Holta.

W porównaniu z metodą prostego wygładzania szeregu czasowego obok parametru α pojawia się parametr β. Jeden z nich pozwala ustalić stały poziom a drugi oznacza przyrost. Też wyznaczamy je prognozami wygasłymi.

Taki model jest wykorzystywany gdy trendu nie da się opisać za pomocą funkcji.

Podobnie jak w tamtym modelu trzeba znać pierwszą prognozę - również jest to pierwsza wartość rzeczywista, natomiast wielkość przybliżająca pierwszy przyrost to jest to różnica pomiędzy 1 i 2 wartością rzeczywistą S₂ = y₂ - y₁. Parametry α i β są z przedziału (0;1) i ulegają w przeciwieństwie do modelu liniowego zmianom.

WYKŁAD 3

Prognozowanie zjawisk z wahaniami okresowymi

Składowa okresowa może występować w postaci wahań cyklicznych, sezonowych i jest ona efektem rytmicznego oddziaływania pewnych przyczyn na zjawisko (z pewną określoną częstotliwością, co pewien przedział czasu). Powodują odchylenia od tej postaci składowej systematycznej jaką jest stały poziom lub trend.

O wahaniach cyklicznych mówimy gdy długość cyklu przekracza rok (np. cykl świński - co 3 lata odbudowywane pogłowia trzody chlewnej, cykle koniunkturalne, cykle owocowe).

Wahania sezonowe - długość cyklu nie przekracza rok, np. tygodniowe, kwartalne, roczne, związane najczęściej ze zmianami kalendarza, zmianami klimatycznymi w ciągu roku.

Obserwacje muszą być prowadzone z odpowiednią częstotliwością. Ważna jest również liczba obserwacji, które prowadzimy. Dane muszą zawierać co najmniej 4 pełne cykle.

Amplituda - odchylenie między wartością maksymalną bądź minimalną a wartością wynikającą ze stałego poziomu lub trendu. Wahania, w których amplitudy nie ulegają zmianie to wahania bezwzględnie stałe:

Zależnie jaki rodzaj wahań jest zidentyfikowany w szeregu czasowym, będziemy wyróżniać 2 modele używane do opisu szeregu czasowego:

1. Addytywny t = 1, ....., n i = 1, ....., r

2. Multiplikatywny t = 1, ....., n i = 1, ....., r

• rzeczywista, a

• teoretyczna wartość prognozowanej zmiennej w momencie lub okresie t w i-tej fazie cyklu,

• wskaźnik sezonowości dla i-tej fazy cyklu,

r - liczba faz cyklu,

- składnik losowy.

Metoda wskaźników

Nasuwa się więc taka idea zbudowania prognozy żeby najpierw wyznaczyć prognozę z trendu, znaleźć efekt oddziaływania czynników sezonowych czyli tych, które periodycznie tu oddziałują i wreszcie znaleźć prognozę właściwą, korygując prognozę z funkcji trendu o efekt działania czynnika sezonowego w odpowiedniej fazie cyklu. Model addytywny - wahania bezwzględnie, model multiplikatywny - wahania względnie stałe.

1. Wyodrębniamy funkcję trendu. To może być również stały poziom.

2. Eliminujemy tendencję rozwojową z szeregu czasowego.

• dla modelu addytywnego odejmujemy od wartości rzeczywistych wartości wynikające z trendu:

• dla modelu multiplikatywnego - dzielenie wartości rzeczywistych przez wynikające z trendu:

3. Należy wyeliminować wahania przypadkowe ζ - policzenie średnich:

Otrzymamy więc ciąg wskaźników surowych z_i dla i = 1, ..., r policzonych dla każdej fazy. Te wskaźniki byłyby czystymi gdyby spełniały następujący warunek:

• dla modelu multiplikatywnego: suma wskaźników wahań powinna być równa liczbie faz w cyklu:

• dla modelu addytywnego suma tych wskaźników powinna być równa 0:

Tak jednak nie jest przede wszystkim na skutek zaokrągleń, a więc należy

4. Wyznaczyć czyste wskaźniki wahań.

Posługujemy się tzw. wskaźnikiem korygującym q, czyli liczymy średni wskaźnik surowy i wówczas:

• przy modelu addytywnym odejmujemy od poszczególnych wskaźników surowych ten wskaźnik q:

• przy modelu multiplikatywnym dzielimy przez średni surowy wskaźnik:

gdzie

Czyste wskaźniki wahań C_i w przypadku modelu multiplikatywnego są wartościami, które zazwyczaj wyrażamy w procentach - są powyżej bądź poniżej 1. Wskaźnik C_i mówi o ile w i-tej fazie cyklu wartości zmiennej były wyższe bądź niższe od trendu z powodu działania czynników sezonowych, np.

C₁ = 0,95 - 95% niższe o 5%

C₂ = 1,05 - 105% czyli wyższe o 5%

W przypadku modelu addytywnego wskaźniki są dodatnie bądź ujemne. Wskaźnik C_i mówi, że w i-tej fazie cyklu wartość zmiennej jest o C_i jednostek niższa lub wyższa od trendu z powodu działania czynników sezonowych.

5. Wyznaczenie prognozy:

• 
  
  model addytywny:

• model multiplikatywny:

Wady modelu - nie można ocenić jakości tego modelu za pomocą np. współczynnika R². Można posłużyć się wskaźnikiem względnego poziomu reszt:

z „daszkiem” gdyż mamy na myśli uwzględnienie efektu sezonowości.

dla modelu addytywnego

dla modelu multiplikatywnego

Kolejna wada - trudności z dobraniem funkcji trendu w pierwszym etapie postępowanie.

Również niedogodnością jest to, że nie ma tu możliwości policzenia błędu ex-ante.

Metoda trendów jednoimiennych

Jest to metoda bardzo wygodna do zastosowania. Jeżeli mamy zjawisko podlegające wahaniom i szereg jest odpowiedniej długości to punkty dotyczące danej fazy możemy dopasować linią trendu. Takie trendy budujemy dla poszczególnych faz cyklu. Dla każdej fazy mamy inne równanie i te proste są dobrze dopasowane to możemy z trendów wyznaczyć prognozę.

Y_ti - wartość zmiennej prognozowanej, f_i(t_i) - funkcja trendu dla i-tej fazy cyklu.

Ta metoda ma jednak jedną poważną wadę - trzeba mieć dużo obserwacji.

Analiza harmoniczna

i - numer harmoniki, t - numer obserw.

Ten przypadek modelu, który tutaj jest zapisany jest taki - składowa systematyczna jest w postaci stałego poziomu, stały poziom jest wyrażony przez parametr α₀ i na stały poziom nakładają się wahania sezonowe. Te wahania sezonowe są wyrażone poprzez hamoniki czyli funkcje sinusoidalne i cosinusoidalne.

Jeżeli szereg czasowy, w którym występują wahania sezonowe chcemy opisać za pomocą harmonik, to tych harmonik w sumie może być n/2. Pierwsza harmonika ma okres o długości n, druga - n/2, trzecia - n/3 itd. gdzie n to długość szeregu czasowego. Trzeba mieć jeszcze oceny α₀, α_i, β_i.

Współrzędne harmonik oceny parametrów α_i, β_i są inne dla każdej harmoniki. Wielkość stałą α₀, wyznaczamy jako średnią:

Natomiast oceny parametrów α_i, β_i wyznacza się z metody najmniejszych kwadratów. Dla harmonik od pierwszej do przedostatniej (czyli dla i = 1, ..., (n/2)-1:

Ocena dla ostatniej harmoniki (n/2) parametr a jest zawsze równy 0, parametr b zaś:

Każda harmonika ma pewne własności - ma odpowiednią amplitudę. Jeżeli mamy już wyznaczone parametry a_i oraz b_i to amplituda dla danej harmoniki:

Jeżeli budujemy model to ni musimy uwzględniać wszystkich harmonik. Każda zmienna ma pewną wariancję S². Ponieważ poszczególne harmoniki są od siebie niezależne to można posłużyć się do wyboru harmoniki częścią ogólnej wariancji zmiennej, którą dana harmonika wyjaśnia. Do modelu ostatecznego możemy wybrać te harmoniki, których wariancje wyjaśniają w dużym stopniu zmienność.

dla i = 1, ..., (n/2)-1

WYKŁAD 4

Prognozowanie na podstawie modeli ekonometrycznych

Poprzednie metody oparte były na szeregach czasowych. Metody prognozowania przyczynowo-skutkowego, a wśród nich model ekonometryczny mają zarówno pewne plusy jak i minusy wobec metod opartych na analizie szeregu czasowego. Plusy są takie, że mamy możliwość zweryfikowania naszych hipotez dotyczących wpływu czynników na oddziaływane zjawisko. Drugi plus wynika z tego, że mogą być narzędziem symulacji.

Symulacje - badanie możliwych stanów istniejącego fragmentu rzeczywistości za pomocą eksperymentowania na modelu.

Kiedy mamy zbudowany model, to możemy sobie np. dobierać zmienne egzogeniczne i w ten sposób odpowiadać na pytanie jakie będą wartości zmiennych endogenicznych. Możemy również zmieniać parametry modelu.

Można też zastanawiać się jakie byłyby wartości zmiennych endogenicznych gdyby zmienne egzogeniczne przyjęły określone wartości zmiennych endogenicznych.

Model ekonometryczny ma też pewne wady - jest bardziej pracochłonny, trzeba mieć dużo danych.

Model ekonometryczny: Y = f(X; E)

Y - wektor zmiennych objaśnianych - czynniki wpływające na zmienną objaśnianą.

X - macierz zmiennych objaśniających

E - wektor składników losowych modelu

Jest to pewna zależność między wyróżnionymi zmiennymi od innych zmiennych.

Model ekonometryczny może być budowany w celach diagnostycznych do określenia prawidłowości między zmiennymi objaśnianymi i objaśniającymi. Może być też budowany do celów prognostycznych - a więc od modelu (danych o przeszłości) trzeba przejść do prognozy (przyszłości).

Modele proste - zbiór modeli jednorównaniowych, z których każdy może być traktowany oddzielnie.

Modele rekurencyjne - prosty jeżeli zachowamy pewną właściwą kolejność szacowania parametrów w modelu. Czyli można tak poprzestawiać równania w tym modelu, że szacując je kolejno uzyskamy informacje z modelu poprzedniego niezbędne do oszacowania parametrów następnego modelu.

Model o równaniach współzależnych - jeżeli przyjmiemy, że jest dwurównaniowy, to w równaniu pierwszym zmienną objaśnianą jest np. objaśniająca w drugim modelu i na odwrót (pętla sprzężenia zwrotnego).

Etapy budowy modelu:

1. Specyfikacja zmiennych - jakie czynniki wpływają na zmienną objaśnianą, jak je dobieramy (np. metoda pojemności informacji). W prognozowaniu interesują nas jednak bardziej zmienne, o których przypuszczamy, że będą oddziaływać w przyszłości na badane zjawisko.

2. Wybór postaci modelu

3. Estymacja parametrów modelu

4. Weryfikacja modelu.

Jeżeli mamy oszacowany model to wielkości które stoją przy zmiennych objaśniających to są współczynniki regresji, które mówią o tym jak zmienna objaśniająca wpływa na zmienną objaśnianą. Zmienne objaśniające wyrażane są w różnych mianach, więc nie należy oceniać znaczenia zmiennej objaśniającej dla zmiennej objaśnianej na podstawie współczynników regresji - nie należy porównywać wartości tych współczynników. Jeśli chcemy określać to znaczenie, można policzyć współczynnik ważności zmiennej objaśnianej:

- średnia arytmetyczna zmiennej objaśniającej x_i

- średnia arytmetyczna zmiennej objaśnianej y

- wartość oceny parametru strukturalnego

Założenia teorii prognozy ekonometrycznej

1. Znany jest „dobry model” ekonometryczny. Dobry model - musi być dobrze dopasowany. Miarą dopasowania jest współczynnik determinacji R²:

Mamy np. 2 modele:

Oraz współczynniki determinacji tych modeli:

To relacja jest taka, że gdy ilość zmiennych w modelu rośnie to poprawia się dopasowanie modelu:

Lepiej stosować współczynnik determinacji z próby (wyrównany - „adjusted”) - on jest lepszy jeżeli chcemy porównywać dopasowanie modeli o różnej ilości zmiennych objaśniających:

n - liczba obserwacji, m - liczba zmiennych objaśniających występujących w modelu.

Dobroć modelu (dopasowanie) ocenia również klasyczna miara - standardowy błąd oceny modelu, jednak jest to miara bezwzględna, stąd chętniej używa się R²:

Dobry to również ten, w którym parametry są istotne. Wprowadzamy więc takie zmienne, które wydają nam się ważne z punktu widzenia zmian zmiennej objaśnianej. Mniej ważne powinny z modelu wypaść.

2. Występuje stabilność relacji strukturalnych w czasie. Jeżeli parametry modelu:

Oszacowaliśmy na podstawie obserwacji z okresu t = 1, 2, ..., n to wyrażają one pewną prawidłowość, która łączyła zmienną objaśniającą x_i ze zmienną objaśnianą y w przeszłości. W przyszłości (w następnych okresach) parametry te muszą być takie same.

3. Składnik losowy ma stały rozkład w czasie

Jest pewną zmienną losową, której rozkład ma:

E(ζ _t) = 0 oraz V(ζ _t) = const

Składnik losowy to taki „worek”, do którego wrzucamy zmienne, których nie rozpoznaliśmy i nie ujęliśmy w modelu. Może się jednak zdarzyć, że zmienne „wymienią się”, tzn. do modelu trafi nowa zmienna ze składnika losowego, a z modelu zniknie inna. W naszym założeniu nie ma to miejsca czyli składnik losowy ma stały rozkład w czasie.

4. Znane są wartości zmiennych objaśniających w okresie/momencie prognozowanym (a więc przyszłe zmienne objaśniające). Źródłem mogą być gotowe prognozy, np. GUS-u, niezależnych instytutów badawczych, mogą być decyzje jednostek nadrzędnych (rządu), które mają być zrealizowane (np. budżet), itp. Można też zrobić prognozy samemu np. metodami opartymi o szeregi czasowe.

5. Można ekstrapolować model poza obszary zmienności zmiennych objaśniających zaobserwowane w próbie.

Załóżmy, że mieliśmy tylko jedną zmienną objaśniającą x₁ i na podstawie tych obserwacji oszacowaliśmy taki model liniowy:

Dla tych obserwacji spoza przedziału model musi być prawdziwy.

Model ekonometryczny stosuje prognosta reprezentujący postawę pasywną. Model jest więc narzędziem do budowy prognoz krótkookresowych.

Za takie szczególnie krępujące możemy uznać założenie 2, mówiące o stabilności relacji strukturalnych. To założenie można ominąć budując tzw. modele z uzmiennionymi parametrami. Zbiór obserwacji dzielimy na pewne podzbiory w taki sposób, że z n obserwacji wyróżnimy zbiory

k-elementowe. Pierwszy model szacujemy na podstawie pierwszych k obserwacji. Później najwcześniejszą obserwację odrzucamy i dodajemy następną i znów szacujemy model. W ten sposób otrzymamy pewien ciąg parametrów modelu, które będą pokazywały zmiany oddziaływania między czynnikami.

W ten sposób możemy uzyskać pewne trendy parametrów, które pokazują zmiany tego oddziaływania i do prognoz wykorzystać prognozy tych parametrów. W ten sposób można wykorzystywać model ekonometryczny również do prognoz średniookresowych.

Przyjmijmy, że mamy model liniowy jednorównaniowy z m zmiennych objaśniających:

Model jest dobrym modelem, pozostałe założenia też są spełnione, więc prognozą będzie warunkowa wartość oczekiwana zmiennej y. Warunkowa, ponieważ x muszą przyjąć przewidywane wartości.

Jeżeli prognozę tak zbudujemy to mówimy, że jest to prognoza wyznaczona na zasadzie nieobciążoności, bo równa wartości oczekiwanej tej zmiennej.

Jak wyznaczymy przyszłą wartość zmiennej, należy ocenić dokładność (dopuszczalność) prognozy. Należy wykorzystać błędy ex-ante. Błąd bezwzględny:

- prognoza zmiennej objaśniającej na okres t (prognozowany)

D²(a_i) - wariancja oceny i-tego parametru. W modelu z dwoma zmiennymi objaśniającymi:

Na przekątnej - wariancje ocen parametrów, poza nią są kowariancje ocen parametrów.

S² - kwadrat standardowego błędu oceny.

Błąd prognozy ex-ante będzie się więc zmniejszał kiedy maleć będzie S. Standardowy błąd oceny modelu zmniejsza się kiedy rośnie liczba obserwacji (n).

Kowariancja (a_i, a_j) wyraża zależność między parametrami czyli wyraża też zależność między zmiennymi objaśniającymi, czyli jeżeli zależność między tymi zmiennymi będzie mniejsza (licznik we współczynniku korelacji) to będzie się musiał zmniejszać błąd ex-ante.

Błąd względny:

Tak wyznaczona prognoza jest to prognoza punktowa. Przedział prognozy w modelu ekonometrycznym wygląda tak samo jak w przypadku prognozy na podstawie funkcji trendu:

W modelach ekonometrycznych występuje podział na modele statyczne i dynamiczne. Dynamiczne to takie, gdzie występują zmienne opóźnione (np. objaśniana). Wówczas bardzo często nie jest spełnione założenie o braku autokorelacji między składnikami losowymi. Jeżeli stosujemy MNK do szacowania parametrów modelu to jest tam założenie, że składniki losowe nie są ze sobą skorelowane. To założenie nie będzie spełnione wówczas gdy w modelu ekonometrycznym występują zmienne z opóźnieniami. Wówczas:

Często tak bywa kiedy badamy zmienne, których oddziaływanie jest bardzo długie. Na przykład gdybyśmy mówili, że interesują nas inwestycje w firmie w roku bieżącym, to prawdopodobnie zależą one od tego, jakie inwestycje zostały poniesione wcześniej. Te wcześniejsze wydatki będą rzutowały na wydatki w kolejnych latach. Wtedy założenie o braku autokorelacji składnika losowego nie zawsze jest spełnione. Do badania czy występuje autokorelacja czy nie może posłużyć test istotności współczynnika korelacji:

A - statystyka testowa, i - rząd opóźnienia, a więc składnik losowy z okresu t jest skorelowany ze składnikiem losowym o i okresów opóźnionych. Opóźnienie zwykle nie jest długie - 1, 2 okresy. Większe nie są uwzględniane.

A ma rozkład t-Studenta o n - i - 2 stopniach swobody.

Jeżeli A ≥ A_α to H₀ odrzucamy, w przeciwnym przypadku utrzymujemy.

Jeżeli przeprowadzimy postępowanie weryfikacyjne i okaże się, że mamy zjawiska autokorelacji składnika losowego w naszym modelu, to do oszacowania modelu powinniśmy użyć innej metody niż KMNK, bo otrzymane wówczas parametry mogą nie mieć pewnych pożądanych własności. Z punktu widzenia prognozowania autokorelacja nie jest groźna, a czasami nawet dobra, bo jest szansa, że zostanie poprawiona precyzja prognozy.

Przyjmijmy, że mamy taki model zmiennej y, która zależy od swoich wartości z okresu wcześniejszego i od wartości pewnej zmiennej objaśniającej x:

Po oszacowaniu równanie będzie wyglądało:

Reszty modelu:

Reszty te będą powiązane ze sobą, więc można zbudować model ekonometryczny składnika losowego:

Wiadomo, że estymatorem składnika losowego są reszty modelu, więc wykorzystując je, oszacujemy oceny parametrów β₀ i β_i i otrzymamy oszacowanie modelu składnika losowego:

Żeby z tego modelu zrobić prognozę składnika losowego na okres t, trzeba mieć reszty opóźnione, które zawsze będziemy mieli:

Gdy z modelu (2) będziemy chcieli zrobić prognozę y na okres t > n, będziemy musieli mieć opóźnioną wartość y_t-1 (nie ma problemu - zawsze mamy) oraz prognozę zmiennej objaśniającej x (musimy znaleźć bądź zrobić tę prognozę):

Symbol ^(w) to tzw. prognoza wstępna. Jeżeli wiemy, że składniki losowe są ze sobą skorelowane, to ostateczną prognozę możemy wyznaczyć jako sumę dwóch prognoz: tego co nazwaliśmy prognozą wstępną (z modelu) i prognozy składnika losowego:

W ten sposób możemy oczekiwać, że ta prognoza będzie nie gorsza niż prognoza wstępna (błąd bezwzględny tej prognozy na pewno nie będzie większy niż prognozy wstępnej). Stąd warto sprawdzić, czy jest autokorelacja składnika losowego.

Zmienne dychotomiczne

Są to zmienne zero-jedynkowe:

1, jeżeli obiekt ma daną cechę

X =

0, jeżeli obiekt nie ma danej cechy

Przypadek I:

Jeżeli budujemy model i w zbiorze zmiennych objaśniających mamy zmienną o takim charakterze, natomiast zmienna objaśniana jest klasycznie rozumianą zmienną ilościową, nie ma żadnego problemu - model szacujemy metodą najmniejszych kwadratów.

Przypadek II:

Zmienną dychotomiczną jest zmienna objaśniana. Jest to gorsza sytuacja. Na przykład:

Badamy n osób, ze względu na:

Y - miejsce spędzania urlopu: kraj: 0, zagranica: 1.

X - wysokość dochodów w tys. złotych.

Gdzie j - numer badanej osoby.

Wówczas oszacowano model:

- wartość jest oszacowaniem warunkowego prawdopodobieństwa realizacji pewnego zdarzenia przy ustalonych wartościach zmiennej objaśnianej x.

Jeżeli dochody podzielimy na pewne przedziały klasowe to będzie to prawdopodobieństwo warunkowe przy założeniu, że x wpada do pewnej grupy.

Dokonuje się transformacji prawdopodobieństwa z przedziału [0,1] na przedział (-∞, +∞). Mówi się o transformacji logitowej i probitowej.

Transformacja probitowa polega na tym, że wartości, które powinny być z przedziału [0, 1] należy przetransformować na przedział (-∞, +∞).

Wracając do przykładu z dochodami, zazwyczaj dochody będziemy dzielić na pewne grupy (klasy). Wprowadzamy więc pewne kategorie zmiennej objaśniającej po to, abyśmy mogli mierzyć częstość wystąpienia danego wariantu zmiennej objaśnianej (0 albo 1). Pod pojęciem transformacji probitowej będziemy rozumieć wówczas przekształcenie częstości wystąpienia danego wariantu w każdej z tych kategorii na dystrybuantę standaryzowanego rozkładu normalnego:

Po zastąpieniu prawdopodobieństw (częstości) probitami nasz model (jest stablicowany). przyjmie postać:

WYKŁAD 5

Prognozowanie przez analogie

Metody wcześniejsze (szeregi czasowe czy modele przyczynowo-skutkowe) nie mogą być zawsze stosowane gdyż są one stosowane tylko wtedy, gdy możemy sądzić, że prawidłowość, która została odkryta w szeregu czasowym czy modelu ekonometrycznym będzie w przyszłości taka jak była.

Jednym z możliwych do zastosowania pojęć jest wykorzystanie analogii.

Analogia - zgodność, podobieństwo pewnych cech między odmiennymi skądinąd przedmiotami, zjawiskami.

Rozumowanie przez analogię - przenoszenie twierdzeń o jednym przedmiocie na inny na podstawie zachodzących między nimi podobieństw.

Rodzaje metod analogowych

1) Metoda analogii biologicznych - przenosimy budowy lub funkcjonowania organizmów żywych na martwe, np. analogia polegająca na tym, że produkowane są lekarstwa, które wykorzystują właściwości roślin.

2) Metoda analogii przestrzennych - przewidywanie zajścia określonego zjawiska na określonym terytorium na podstawie zajścia takiego zdarzenia gdzie indziej, np. w Polsce banki wprowadzają karty kredytowe, gdyż sprawdziło się to w innych państwach. Jeżeli w Afryce pojawiło się AIDS to wiadomo było, że będzie się rozpowszechniać w innych krajach.

3) Metoda analogii historycznych - przewidywanie przyszłych stanów jednych zmiennych na podstawie przeszłych stanów innych zmiennych opisujących ten sam obiekt co zmienne prognozowane. Np. cykl życia proszku do prania w tabletkach będzie analogiczny do cyklu życia zwykłego proszku.

4) Metoda analogii przestrzenno-czasowych - przewidywanie przyszłych stanów zmiennej opisującej prognozowany obiekt na podstawie przeszłych stanów tych samych co do istoty zmiennych opisujących inne obiekty.

Do prognozowania wykorzystuje się dwie ostatnie metody, gdyż mamy skłonności do naśladowania, przynajmniej jeśli chodzi o dobra wyższego rzędu.

Ad 4) Analogie przestrzenno-czasowe

Co będziemy rozumieć pod pojęciem podobieństwa - kryteria podobieństwa:

1. Podobieństwo poziomu - o dwóch zmiennych będziemy mówili, że są podobne w sensie podobieństwa poziomu jeżeli kiedykolwiek osiągnęły tą samą wartość, ten sam poziom:

Gdzie y - badana zmienna, o - obiekt badany, k - obiekt, z którym porównujemy.

W dwóch różnych momentach czasu zmienna w obu obiektach osiągnęła w przybliżeniu tę samą wartość.

2. Podobieństwo kształtu - dwie zmienne są podobne w sensie podobieństwa kształtu gdy charakteryzują się podobną dynamiką, tj. mają podobne tendencje rozwojowe, wahania cykliczne czy sezonowe.

Miary podobieństwa funkcji.

Mamy dwa szeregi czasowe. Do mierzenia podobieństwa możemy wykorzystać współczynnik korelacji (r) albo tzw. miarę podobieństwa funkcji (m) (oba wskaźniki przyjmują wartości z przedziału [0,1]).

Patrząc na te dwie proste wydaje się, że są one podobne ale to podobieństwo nie jest takie idealne. Wartość miary podobieństwa jest mniejsza niż współczynnik korelacji, co oznacza, że to podobieństwo w sensie miary jest mniejsze i wydaje się, że miara lepiej to oddaje.

Z kolei w tym przypadku jeden z szeregów ma „zęby” spowodowane działaniem przyczyn przypadkowych ale generalnie tendencja zarówno jednego jak i drugiego szeregu jest bardzo podobna. Współczynnik korelacji pokazuje, że rzeczywiście to podobieństwo jest znaczne, ale miara podobieństwa pokazuje, że tego podobieństwa praktycznie nie ma.

Jeżeli taka sytuacja występuje to to by znaczyło, że obie miary dają rozbieżne wyniki. Żeby temu zapobiec to przed policzeniem miary należałoby wygładzić szereg czasowy, np. średnią ruchomą. Wtedy wskazania miar będą lepsze.

Które podobieństwo - poziomu czy kształtu?

1) Przyjęcie podobieństwa w sensie poziomu oznacza przyjęcie założenia, że po osiągnięciu pewnego poziomu (stanu nasycenia), zjawiska w różnych obiektach powinny zmieniać się tak samo, jeżeli chcemy mówić, że są podobne. Jeżeli np. 20 lat temu w Niemczech nasycenie samochodami było takie, że przypadało 50 samochodów na 100 gospodarstw domowych, a potem, załóżmy, co roku ta liczba się podwajała, to jeżeli w tym roku zanotujemy w Polsce taki sam wynik - 50 samochodów na 100 gospodarstw, to będziemy oczekiwali takich samych zmian zjawiska w latach następnych. To założenie jest bardzo mocne i nie zawsze będzie spełnione.

2) Dlatego wydaje się, że lepszym kryterium podobieństwa jest kryterium kształtu, gdyż wymaga porównania tylko dwóch wielkości.

Jak się wyznacza m:

c

Liczenie miary podobieństwa polega na porównywaniu kolejnych fragmentów szeregu czasowego. Na rysunku mamy po trzy obserwacje zmiennej dla obiektu badanego p(o) i tego, z którym porównujemy p(k). Bierzemy pierwszy fragment szereg dla obiektu o, przesuwamy go równolegle, przesuwamy również ten fragment dla obiektu k i mierzymy kąt pomiędzy nimi. Miara łukowa tego kąta jest później wykorzystywana do określenia miary podobieństwa między pierwszymi wybranymi odcinkami. Następnie bierzemy kolejny odcinek i określamy drugą miarę łukową. W ten sposób porównywane są podobieństwa wszystkich odcinków składających się na wybrany fragment szeregu czasowego i te wielkości, które wtedy oznaczone są m_i w sumie dają (średnia) ogólną miarę podobieństwa m.

Budowa prognozy przy wykorzystaniu podobieństwa poziomu (graficznie):

W momencie t” wystąpiła w obiekcie o ta sama wartość co w obiekcie k. Jeżeli stwierdziliśmy takie podobieństwo to budowa prognozy polega na tym, że do szeregu czasowego obiektu prognozowanego doklejamy ten fragment szeregu czasowego jaki wystąpił w obiekcie k.

Budowa prognozy przy wykorzystaniu podobieństwa kształtu (graficznie):

Budowa prognozy również polega na doklejeniu tego fragmentu szeregu czasowego, który wystąpił w obiekcie podobnym w okresie podobieństwa. Zwrócić uwagę należy na różnicę poziomów - doklejamy ten fragment do tej wartości, która była zanotowana w obiekcie o w ostatnim okresie. Wykorzystujemy tylko kształt.

Postępowanie zmierzające do wyznaczenia prognozy przy wykorzystaniu analogii przestrzenno-czasowych może być przedstawione w kilku etapach:

1. Określenie wstępnej listy obiektów określonych na podstawie podobieństwa obiektów ze względu na warunki kształtowania się zmiennej prognozowanej. Np. Polski nie porównujemy z Japonią.

2. Pomiar podobieństwa obiektów wg wybranego kryterium lub obu kryteriów łącznie oraz ustalenie zbioru obiektów podobnych. Jeżeli tych obiektów będzie kilka to budujemy prognozę zjawiska według kilku tych obiektów (y(o₁), y(o₂), itd.). Mówi się wówczas, że budujemy prognozy cząstkowe - prognozy zmiennej na podstawie danych o pojedynczym obiekcie podobnym.

3. Wyznaczenie prognozy cząstkowej. Prognozą jest fragment szeregu czasowego podobnego obiektu następujący po jego przedziale podobieństwa, ewentualnie z uwzględnieniem przesunięcia poziomu.

Obserwacje	Numer obserwacji
		...	-2	-1	0	+1	+2	...
yt(o)	...	y-2(o)	y-1(o)	y0(o)
yt(k)		y-2(k)	y-1(k)	y0(k)	y1(k)	y2(k)

Mamy szeregi czasowe dwóch zmiennych - szereg czasowy zmiennej y w obiekcie prognozowanym (o) i szereg czasowy tej samej zmiennej w obiekcie k. Przenumerujmy te okresy - takie wprowadźmy numery okresów, że ostatni okres, z którego pochodzi najnowsza wartość w obiekcie prognozowanym (o) będzie miał numer 0 (punkt startu do wyjścia w przyszłość). Ostatnia wartość obiektu prognozowanego to y₀(o). Badamy podobieństwo z szeregiem czasowym obiektu k i ten szereg tak przesuwamy, żeby fragmenty podobne się pokryły. Ta wartość, która będzie kończyła przedział podobieństwa w obiekcie k, jest tak usytuowana, że po niej występują pewne wartości. I te wartości stanowią dla nas prognozę dla obiektu o. Przy czym z reguły jest taka sytuacja, że trzeba uwzględnić pewne przesunięcie poziomu:

4. 
   Jeżeli prognoz cząstkowych jest kilka, to wyznaczamy wtedy jedną prognozę globalną czyli jedną wielkość, którą jest średnia prognoz cząstkowych z użyciem wag proporcjonalnych do wartości miar podobieństwa (większą wagę nadajemy tej prognozie cząstkowej, która została wyznaczona na podstawie szeregu czasowego tego obiektu, który był bardziej podobny do obiektu prognozowanego:

5. Ocenić dopuszczalność prognozy.

Tu nie można policzyć błędu ex-ante. Pozostaje nam błąd ex-post bądź dokonanie oceny prognozy przez eksperta lub też ocenę prognozy pozostawić prognoście. Wówczas uwagę zwraca się na długość fragmentu, który był wybierany do badania podobieństwa i na wartości miary podobieństwa.

Ad 3) Analogie historyczne

Wykorzystanie analogii historycznych wymaga podzielenia zmiennych na 2 zbiory. Wyróżnia się zmienne wiodące i naśladujące.

Zmienna wiodąca - taka zmienna, która doznaje zmian w czasie wcześniej niż inna zmienna.

Zmienna naśladująca - taka zmienna, która doznaje zmian w czasie później niż zmienna wiodąca.

Jeżeli taka sytuacja występuje to możemy zbudować prognozę.

Interesują nas dwie zmienne. Jedna wiodąca, druga naśladująca. Zbudowanie prognozy można wówczas podzielić na pewne etapy.

1. Wybieramy odpowiedni miernik podobieństwa d oraz obieramy taką jego wartość krytyczną d*, że jeżeli zostanie ona co najmniej osiągnięta, to naszym zdaniem będzie to świadczyć o istnieniu podobieństwa zmiennych X i Y.

2. Obieramy przedział, z którego ma pochodzić ostatni dostatecznej długości fragment szeregu czasowego zmiennej prognozowanej (naśladującej).

3. Obliczamy wartości miernika podobieństwa tego fragmentu z fragmentami tej samej długości szeregu czasowego zmiennej X, przesuwając w każdym kroku fragment szeregu zmiennej X o jeden okres „w tył. Otrzymujemy wartości miernika podobieństwa: d_-1, d_-2, ..., d_-s

gdzie d_-p - wielkość miernika podobieństwa fragmentu zmiennych X i Y z przesunięciem o p jednostek czasu, p = 1, 2, ..., s.

4. Znajdujemy maksymalną wartość miernika podobieństwa i jeżeli jest spełniona relacja max d_-p ≥ d to zmienną X uznajemy za wiodącą względem zmiennej Y z wyprzedzeniem p.

Przedziały, w których wystąpiło maksymalne i wystarczające podobieństwo nazywamy przedziałami podobieństwa i oznaczamy je dla zmiennej Y - p^(o), dla zmiennej X - p^(k). Długości tych przedziałów są jednakowe.

5. Budujemy model wiążący zmienną naśladującą ze zmienną wiodącą, uwzględniamy wyżej uzyskane opóźnienia p:

Jeżeli do wyznaczenia przyszłej wartości zmiennej naśladującej będziemy wykorzystywać wartości zmiennej wiodącej z okresów poprzednich to znamy jakby wartości zmiennej objaśniającej (warunek dla modelu ekonometrycznego, który tutaj tworzymy).

Może być też model, w którym mamy kilka zmiennych objaśniających (wiodących):

Możemy ten zbiór zastąpić wskaźnikiem syntetycznym x':

Gdzie x_it to wartości znormalizowane:

Takie syntetyczne wskaźniki są często budowane i jeśli są budowane na podstawie zmiennych wiodących to są nazywane „barometrami koniunktury”. W polskiej praktyce takich wskaźników jest dużo. Jednym z najbardziej popularnych (dlatego że jest podawany przez „Rzeczpospolitą”) jest tzw. wskaźnik wyprzedzający koniunktury, który przenosi informacje o przyszłych tendencjach w gospodarce. Jest budowany na podstawie 8 składowych, które są normalizowane.

Tego typu podejście oparte na analogiach historycznych jest wykorzystywane często przy prognozowaniu cyklu koniunkturalnego. W różnych krajach są różne jego długości, stąd poprzednie metody zawodzą, w metodach modelowania przyczynowo-skutkowego trudno zdefiniować jakie są przyczyny, że występują cykle koniunkturalne. To podejście zostało zapoczątkowane w Stanach Zjednoczonych. Tam oprócz zmiennych naśladujących i wiodących są też zmienne zbieżne - takie, które zmieniają się jednocześnie.

Praca pochodzi z serwisu www.e-sciagi.pl

1

Zdarzenia znane

Zdarzenia nieznane

Należące do przeszłości

Należące do przyszłości

Przewidywanie przyszłości

Racjonalne

Nieracjonalne

Zdroworozsądkowe

Naukowe

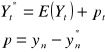
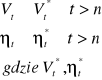
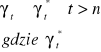
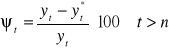
Tendencja rozwojowa

Stały (średni) poziom

Przypadkowa

Sezonowe

Składowe szeregów czasowych

Wahania okresowe

Cykliczne

Systematyczna

Cykl (okres) wahań

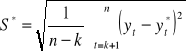
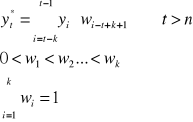
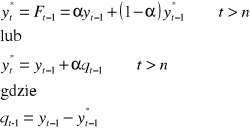
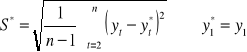
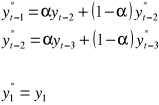
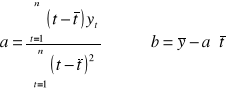
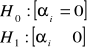
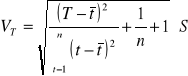
p

y

t

1 2 n-1 n

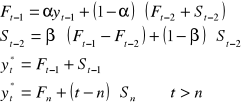
Amplituda

Pełny cykl

Amplitudy się zmieniają -

- wahania względnie stałe

Stałe amplitudy -

- wahania bezwzględnie stałe

n n+1

y_t

t

1

Prognoza wyznaczona z trendu

Prognoza uwzględniająca efekt działania czynników sezonowych

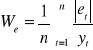
...min 32 dla 4-fazowego cyklu aby było 8 obserwacji dla fazy (aby obliczyć 4 trendy).

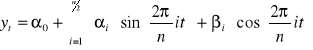
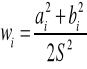
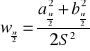
p(k)

p(o)

Y

X

Zmienna naśladująca - możemy ją tak nazwać jeśli po odpowiednim przesunięciu w lewo pokryje się mniej więcej ze zmienną wiodącą

Wielorównaniowe

O równaniach współzależnych

Rekurencyjne

Proste

Jednorównaniowe

Modele ekonometryczne

Zmienna wiodąca

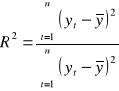
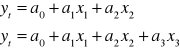
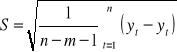
x₁

y

Tylko w tym obszarze ta relacja jest prawdziwa

X

Dla tej obserwacji model nie

musi być prawdziwy

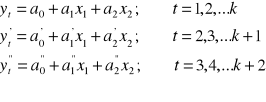
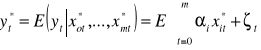
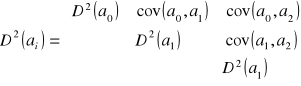
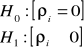
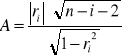
prawdopodobieństwo

1

0,5

t

y^(o), y^(k)

y^(k)

y^(o)

t'

t”

p(o)

t'

t”

t

p(k)

p(o)

m^(0,k) ≥ m*

m - miara podobieństwa

30⁰

r = +1

m = 0,66

m = -0,01

r = 0,8

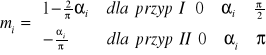
f(a₁)

t

a₁ a₂ a₃

c₁ c₂ c₃

p(o)

p(k)

prognoza

przeszłość

to samo

y^(o)

y^(k)

y^(o), y^(k)

t

t”

Podobieństwo w przeszłości

t

t”

t'

Prognoza

to samo

y^(o)

y^(k)

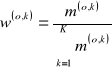
t

y

---