UKŁADY TRÓJFAZOWE

Źródła, w których wytwarzane są napięcia sinusoidalne o jednakowej częstotliwości, jednakowej amplitudzie, a poprzesuwane o ten sam kąt względem siebie, noszą nazwę generatorów (prądnic) wielofazowych symetrycznych. Na szczególną uwagę zasługują symetryczne generatory (prądnice) trójfazowe. Generator trójfazowy symetryczny, a takim będziemy się zajmować, wytwarza napięcia fazowe sinusoidalne o tej samej częstotliwości (częstotliwość przemysłowa w Polsce i Europie wynosi 50 Hz), tej samej amplitudzie, a poprzesuwane względem siebie w fazie o 120⁰ (1/3 okresu w czasie). Układy trójfazowe należą do najbardziej rozpowszechnionych w energetyce.

W wykładzie tym zostaną omówione zagadnienia teoretyczne związane z układami trójfazowymi. Dla symetrycznego generatora trójfazowego napięcia w poszczególnych fazach są poprzesuwane względem siebie o 120⁰ (1/3 okresu - T). Fazy generatora oznaczamy literami A, B, C. Poszczególne napięcia fazowe generatora mają postać:

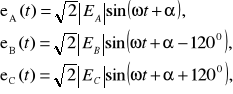
(13.1)
przy czym

.

Jedną z faz, zazwyczaj fazę A, przyjmujemy jako tzw. fazę odniesienia. Układ trójfazowy, w którym napięcia fazowe e_A, e_B, e_C opisane są równaniem (13.1), nosi nazwę układu kolejności zgodnej. Na podstawie zależności (13.1) można zauważyć, że dla symetrycznego układu napięć trójfazowych dla każdej chwili czasu t spełnione jest równanie

.

(13.2)

Jeżeli przebiegom czasowym (13.1) przyporządkujemy wartość skuteczną zespoloną, to mają one postać:

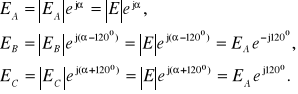
(13.3)

Dla wartości skutecznych zespolonych również zachodzi zależność

E_A + E_B + E_C = 0.

Napięcia fazowe symetrycznej prądnicy trójfazowej przedstawiono na rys.13.1a w postaci czasowej, a na rys 13.1b odpowiadający im wykres wektorowy, dla α=0.

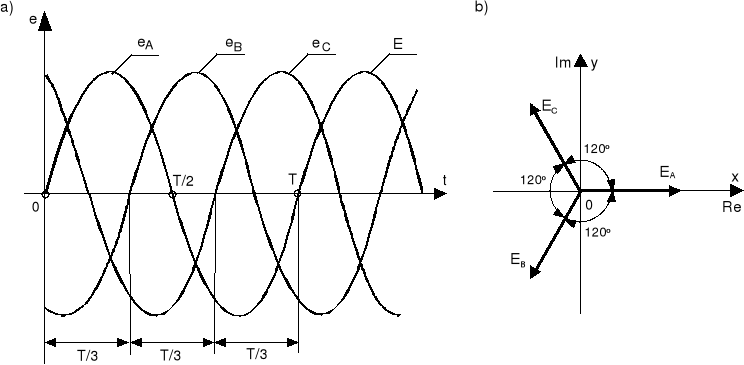
Rys.13.1. Napięcia źródłowe wytwarzane w symetrycznej prądnicy trójfazowej: a) przebiegi chwilowe dla poszczególnych faz; b) wykres wektorowy

Napięcia źródłowe generatora można kojarzyć (łączyć) w gwiazdę lub trójkąt. Podobnie można kojarzyć odbiornik. W zależności od skojarzenia generatora i odbiornika rozróżniamy układ trójfazowy: gwiazda - gwiazda, trójkąt - gwiazda, gwiazda - trójkąt, trójkąt - trójkąt.

Przy połączeniu gwiazda - gwiazda wyróżniamy układ trójprzewodowy (bez przewodu zerowego) lub układ czteroprzewodowy z przewodem zerowym (neutralnym).

13.1. Analiza układu trójfazowego gwiazda - gwiazda

Rozważmy najpierw układ gwiazda - gwiazda trójprzewodowy, bez przewodu zerowego przedstawiony na rys.13.2.

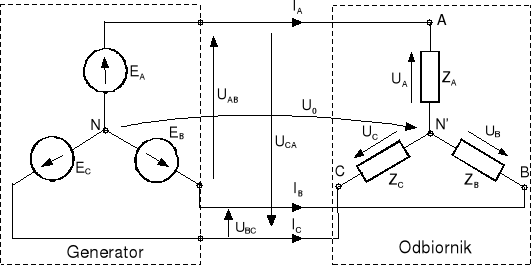
Rys.13.2. Układ trójfazowy gwiazda-gwiazda bez przewodu zerowego

Napięcia E_A, E_B, E_C nazywamy napięciami fazowymi generatora, a napięcia U_A, U_B, U_C nazywamy napięciami fazowymi odbiornika. Prądy płynące w fazach generatora i odbiornika w tym przypadku nazywamy prądami liniowymi (fazowymi) I_A, I_B, I_C. Impedancje Z_A, Z_B, Z_C, tworzą gwiazdę impedancji odbiornika. Napięcia między przewodami fazowymi nazywamy napięciami międzyfazowymi lub napięciami liniowymi i oznaczamy je przez U_AB, U_BC, U_CA.

Dla generatora symetrycznego przedstawionego na rys.13.2 pomiędzy napięciami fazowymi a międzyfazowymi zachodzą zależności:

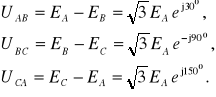
(13.4)

Analizując wzory (13.4) można zauważyć, że napięcia U_AB, U_BC, U_CA tworzą boki trójkąta równobocznego. Na rys.13.3 przedstawiono wykres wektorowy napięć fazowych generatora i napięć międzyfazowych, dla
.

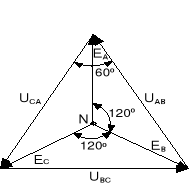
Rys.13.3. Wykres wektorowy napięć fazowych i napięć międzyfazowych symetrycznego generatora trójfazowego

Dla układu przedstawionego na rys.13.2 punkt skojarzenia odbiornika N^' tworzy węzeł, więc dla każdej chwili czasu t spełnione jest I prawo Kirchhoffa

i_A(t) + i_B(t) + i_C(t) = 0 (13.5)

lub dla wartości skutecznych zespolonych

I_A + I_B + I_C = 0 . (13.6)

Przeprowadźmy analizę układu przedstawionego na rys.13.2 przy założeniu, że dane są napięcia fazowe symetrycznego generatora oraz impedancje odbiornika. Szukanymi wielkościami są prądy fazowe, napięcia fazowe odbiornika oraz moce występujące w rozpatrywanym układzie.

Jeżeli przez U_N'N = U₀ oznaczymy napięcie pomiędzy punktem skojarzenia generatora N i odbiornika N^', to napięcia fazowe odbiornika można zapisać w postaci

U_A = E_A - U_N'N = E_A - U₀ ,

U_B = E_B - U_N'N = E_B - U₀ , (13.7)
U_C = E_C - U_N'N = E_C - U_{0 .}

Natomiast prądy fazowe wyrażamy za pomocą zależności

I_A = Y_A U_A,

I_B = Y_B U_B, (13.8)
I_C = Y_C U_C.

Aby wyznaczyć te wielkości, należy wyznaczyć napięcie U₀. Napięcie to wyznaczymy za pomocą metody napięć węzłowych. Potencjał węzła N przyjmujemy jako równy zero i wówczas:

U₀ (Y_A+Y_B+Y_C) =Y_AE_A + Y_BE_B + Y_CE_C ,

stąd

. (13.9)

Wstawiając zależność (13.9) do (13.7) obliczamy napięcia fazowe, a następnie prądy fazowe (13.8). Analizując wzór (13.9), można zauważyć, że jeżeli Y_A=Y_B=Y_C=Y, to napięcie U₀ przyjmuje postać

.

Układ trójfazowy, dla którego U₀ = 0, nosi nazwę układu symetrycznego. Dla układu symetrycznego napięcia fazowe generatora są równe napięciom fazowym odbiornika (por.wzór 13.7), natomiast prądy I_A, I_B, I_C mają te same wartości skuteczne i są poprzesuwane względem siebie o 120⁰. Wykres wektorowy napięć fazowych generatora, odbiornika i prądów odbiornika dla układu symetrycznego przedstawiono na rys. 13.4. Kąt fazowy ϕ jest kątem fazowym admitancji odbiornika (ϕ_A = ϕ_B = ϕ_C = ϕ , Y = Ye^-jϕ).

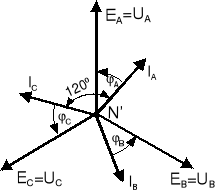
Rys.13.4. Wykres wektorowy napięć fazowych generatora i odbiornika oraz prądów dla układu trójfazowego symetrycznego trójprzewodowego przy połączeniu gwiazda-gwiazda

Moc chwilowa źródła dla dowolnego obciążenia określona jest zależnością

p_E(t) = p_EA(t) + p_EB(t) + p_EC(t) = e_A(t)i_A(t) + e_B(t)i_B(t) + e_C(t)i_C(t). (13.10)

Moc ta jest równa mocy chwilowej odbiornika określonej jako

p₀(t) = u_A(t)i_A(t) + u_B(t)i_B(t) + u_C(t)i_C(t) .

Wartość średnia za okres z mocy chwilowej (13.10) jest mocą czynną P.

. (13.11)

Moc czynną źródła można określić również jako superpozycję mocy fazowych, a mianowicie

P_E = P_EA + P_EB + P_EC = E_A I_A cosϕ_A + E_B I_B cosϕ_B + E_C I_C cosϕ_C ,

gdzie: ϕ_A, ϕ_B, ϕ_C - oznaczają kąty fazowe pomiędzy napięciem fazowym (źródła) generatora a prądem fazowym źródła dla poszczególnych faz.

Ponieważ musi zachodzić bilans mocy czynnych, to moc ta jest równa mocy czynnej odbiornika

P_O = P_OA + P_OB + P_OC = U_A I_A cosϕ_OA + U_B I_B cosϕ_OB + U_C I_C cosϕ_OC ,

gdzie: ϕ_OA, ϕ_OB, ϕ_OC - oznaczają kąty fazowe pomiędzy napięciem fazowym odbiornika a prądem fazowym odbiornika dla poszczególnych faz.

Oprócz mocy czynnej, wyróżniamy moc symboliczną S, która również spełnia zasadę bilansu. Moc symboliczna źródła określona jest w następujący sposób:

, (13.12)
gdzie:

I^* - oznacza wartość skuteczną zespoloną sprzężoną prądu,

Q_E - oznacza moc bierną źródła.

Podobnie będzie określona moc symboliczna odbiornika

. (13.13)

Moc bierna źródła określona jest za pomocą następujących zależności

Q_E = Q_EA + Q_EB + Q_EC = E_A I_A sinϕ_A + E_B I_B sinϕ_B + E_C I_C sinϕ_C. (13.14)

Podobnie moc bierna odbiornika

Q_O = Q_OA + Q_OB. + Q_OC = U_AI_Asinϕ_OA + U_BI_Bsinϕ_OB. + U_CI_Csinϕ_OC .(13.15)

Moce: czynna, bierna, symboliczna są mocami zachowawczymi, czyli podlegają bilansowaniu, natomiast moc pozorna zdefiniowana w następujący sposób

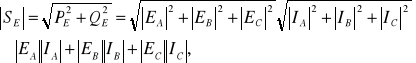
(13.16)

nie spełnia zasady bilansu.

Podobnie dla odbiornika

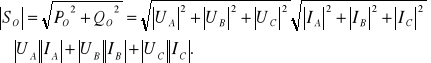
(13.17)

Moc pozorna, jako iloczyn dwóch wartości skutecznych ( S = UI ), nie może podlegać bilansowi, gdyż ogólnie nie zachodzi addytywność dla wartości skutecznych. Moc symboliczna, którą można odwzorować jako wektor, jest sumą wektorów (poszczególnych mocy symbolicznych), czyli
. Natomiast na ogół nie jest spełniona zależność
, wynika to z faktu, że długość wektora wypadkowego nie jest sumą długości wektorów składowych.

Oczywiście, zachodzi zależność

S_E = S_O .

Rozważmy obecnie układ, w którym punkty skojarzenia źródła i odbiornika połączymy za pomocą przewodu o admitancji Y₀, wówczas otrzymamy układ trójfazowy gwiazda-gwiazda czteroprzewodowy. Rozwiązanie takie przedstawiono na rys.13.5. Analiza tego obwodu jest podobna do analizy obwodu z rys.13.2. W mocy pozostają zależności (13.7) oraz (13.8). Natomiast napięcie U₀ wyznaczymy teraz z zależności

. (13.18)

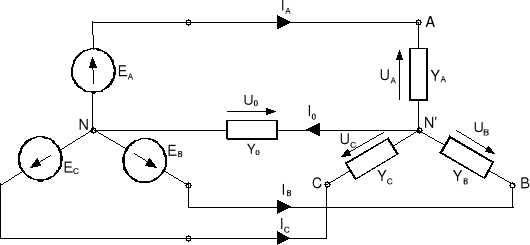
Rys.13.5. Układ trójfazowy gwiazda-gwiazda z przewodem zerowym (neutralnym)

Jeżeli Y_A ≠ Y_B ≠ Y_C, to mamy układ niesymetryczny i wówczas

I_A + I_B + I_C = I₀ . (13.19)

Prąd I₀ jest prądem, który płynie w przewodzie zerowym (neutralnym). Jeżeli impedancja przewodu neutralnego jest równa zero (Y₀ = ∞ ), to U₀ = 0 i odpowiednie napięcia fazowe źródła i odbiornika są sobie równe. Jeżeli mamy do czynienia z układem symetrycznym, tzn. gdy spełniony jest warunek Y_A = Y_B = Y_C = Y, to bez względu na to, czy istnieje przewód zerowy, czy nie (tzn. Z₀ = 0 - zwarcie punktów NN′, Z₀ ≠ 0 - skończona impedancja w przewodzie zerowym, Z₀ = ∞ - brak przewodu zerowego), to dla prądów spełniona jest zależność

I_A + I_B + I_C = 0 . (13.20)

Równania mocy dla układu przedstawionego na rys.13.5 mają postać:

• dla źródła moc symboliczna określona jest zależnością (13.12),

• dla odbiornika

, (13.21)

, (13.22)

. (13.22a)

13.2. Analiza układu trójkąt-trójkąt

Połączenie tego typu przedstawiono na rys.13.6.

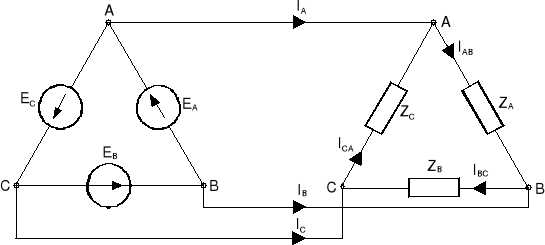
Rys.13.6. Układ trójfazowy trójkąt-trójkąt

W układzie tym napięcia fazowe odbiornika są równe napięciom fazowym generatora i są jednocześnie napięciami liniowymi. Prądy fazowe odbiornika w tym przypadku obliczamy z prawa Ohma

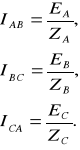
(13.23)

Natomiast prądy przewodowe (liniowe) obliczamy na podstawie I prawa Kirchhoffa

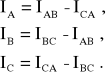
(13.24)

Należy zauważyć, że mając prądy fazowe (13.23), można wyznaczyć prądy przewodowe (13.24). Natomiast mając prądy przewodowe, nie można wyznaczyć prądów fazowych, ponieważ jest to układ zależny poprzez I prawo Kirchhoffa, czyli są tylko 2 równania niezależne, z których bez warunku dodatkowego nie można wyznaczyć trzech wielkości.

13.3. Analiza układów mieszanych

Rozważmy układ trójfazowy przedstawiony na rys.13.7, w którym generator połączony jest w gwiazdę, a odbiornik w trójkąt.

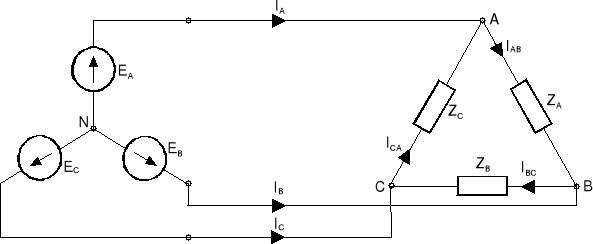
Rys.13.7. Układ trójfazowy mieszany: generator połączony w gwiazdę, odbiornik w trójkąt

W układzie tym napięcia fazowe odbiornika są równe napięciom międzyfazowym generatora. Prądy fazowe odbiornika obliczamy zgodnie z zależnościami

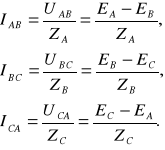
(13.25)

Prądy przewodowe obliczamy jako różnicę odpowiednich prądów fazowych

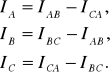
(13.26)

Innym układem trójfazowym mieszanym przedstawionym na rys.13.8 jest układ, w którym generator połączony jest w trójkąt, a odbiornik w gwiazdę.

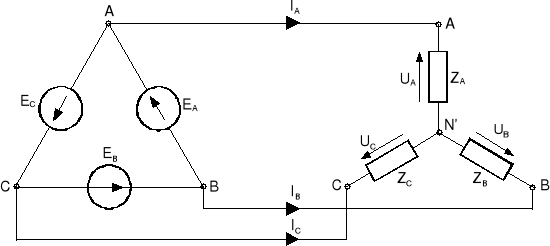
Rys.13.8. Układ trójfazowy mieszany: generator połączony w trójkąt, odbiornik w gwiazdę

Aby wyznaczyć prądy I_A, I_B, I_C oraz napięcia fazowe odbiornika U_A, U_B, U_C należy ułożyć dwa równania wynikające z II prawa Kirchhoffa oraz bilans prądów w węźle N′.

E_A = Z_AI_A - Z_BI_B , (13.27)

E_B = Z_BI_B - Z_CI_C , (13.28)

I_A + I_B + I_C = 0 . (13.29)

Z równania (13.29) wyznaczamy prąd I_C, który wstawiamy do równania (13.28) i otrzymujemy

E_B = (Z_B + Z_C)I_B + Z_CI_A . (13.30)

Wyliczając prąd I_A z równania (13.27) i wstawiając go do równania (13.30), po prostych przekształceniach otrzymujemy postać prądu I_B, a następnie kolejno prądy I_A, I_C:

, (13.31)

, (13.32)

. (13.33)

Napięcia fazowe wyznaczamy z zależności:

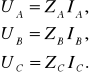
(13.34)

13.4. Pomiar mocy czynnej biernej i pozornej w układach trójfazowych

13.4.1. Pomiary w układach symetrycznych

Rozważmy układ trójfazowy symetryczny czteroprzewodowy przedstawiony na rys.13.9 i przeprowadźmy analizę pomiaru poszczególnych mocy.

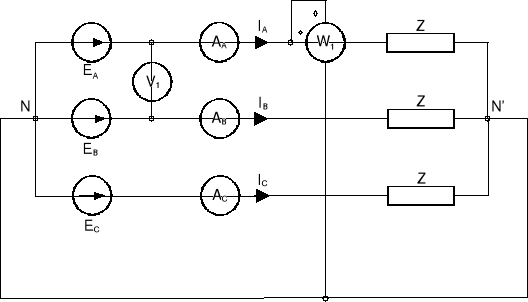
Rys.13.9. Pomiar mocy czynnej w układzie trójfazowym symetrycznym czteroprzewodowym

Dla odbiornika symetrycznego przedstawionego na rys.13.9 zarówno napięcia fazowe odbiornika, jak i prądy liniowe tworzą symetryczną gwiazdę. Kąt przesunięcia pomiędzy napięciami fazowymi odbiornika a prądami liniowymi w każdej fazie jest taki sam, tzn. ϕ_A=ϕ_B=ϕ_C=ϕ. Na rys.13.10 przedstawiony jest wykres wektorowy napięć i prądów dla odbiornika symetrycznego o charakterze rezystancyjno-indukcyjnym (prąd opóźnia się za napięciem fazowym).

Dla rozpatrywanego układu spełnione są również równości:

, (13.35)

. (13.36)

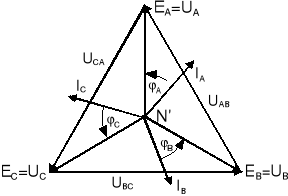
Rys. 13.10. Wykres wektorowy prądów i napięć dla układu trójfazowego symetrycznego

Wykorzystując zależności (13.35), (13.36) można zauważyć, że do pomiaru mocy czynnej wystarczy użyć jednego watomierza, wpiętego tak jak to ilustruje rys.13.9. Wskazanie watomierza wynosi

. (13.37)

Watomierze wpięte w pozostałe fazy i przewód neutralny wskazywałyby tę samą wartość, stąd całkowita moc czynna układu wynosi

, (13.38)

gdzie:
- napięcie międzyfazowe.

Moc bierną wyznaczymy z zależności

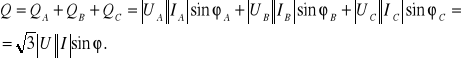
(13.39)

Pomiaru mocy biernej dla układu przedstawionego na rys.13.9 można dokonać za pomocą jednego watomierza w układzie pomiarowym przedstawionym na rys.13.11. Tak włączony watomierz (tzn. cewka prądowa w fazie A natomiast cewkę napięciową łączymy pomiędzy fazy B i C), spełnia rolę waromierza (przyrządu do pomiaru mocy biernej).

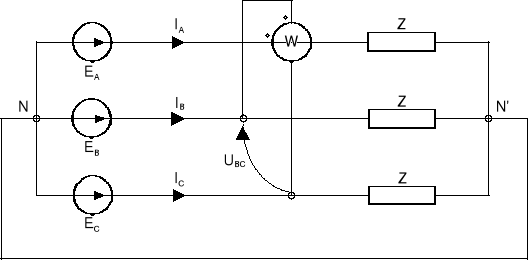
Rys.13.11. Układ do pomiaru mocy biernej w układzie trójfazowym symetrycznym

< (U_BC I_A) . (13.40)

Przekształcenia wzoru (13.40) dokonamy posługując się wykresem wektorowym (rys.13.12)

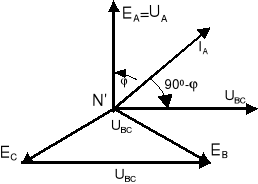
Na podstawie wykresu przedstawionego na rys.13.12 wzór (13.40) można przekształcić do postaci

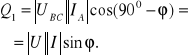
(13.41)

Zatem całkowitą moc bierną pobieraną przez odbiornik symetryczny uzyskujemy mnożąc wartość Q₁ przez
, czyli

Rys.13.12. Wykres wektorowy ilustrujący zasadę pomiaru mocy biernej w układzie trójfazowym symetrycznym

. (13.42)

Moc pozorną pobieraną przez odbiornik wyznaczymy z zależności

. (13.43)

Z zależności (13.43) wynika, że aby wyznaczyć moc pozorną S  wystarczy pomierzyć napięcie międzyfazowe oraz prąd fazowy i iloczyn ich wartości pomnożyć przez
. Jeżeli układ jest symetryczny, lecz trójprzewodowy, pomiaru mocy biernej dokonujemy według zasady przedstawionej na rys. 13.11, natomiast moc czynną mierzymy za pomocą jednego watomierza stosując tzw. sztuczne zero lub za pomocą dwóch watomierzy według układu Arona. Pomiar za pomocą jednego watomierza z wykorzystaniem sztucznego zera przedstawiono na rys. 13.13. Watomierz traktujemy jako idealny (rezystancja cewki napięciowej równa nieskończoności, natomiast rezystancja cewki prądowej równa zero), rezystory tworzące sztuczne zero mają tę samą wartość.

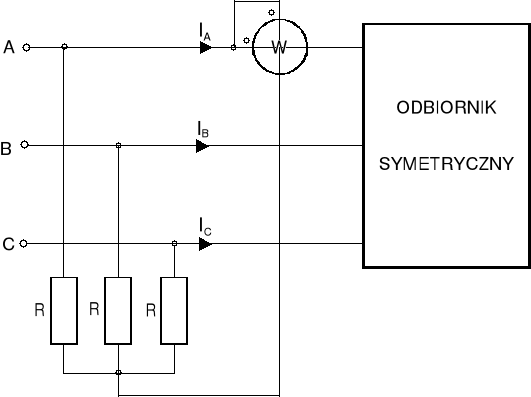
Rys.13.13. Układ do pomiaru mocy czynnej w układzie trójfazowym symetrycznym z wykorzystaniem sztucznego zera

13.4.2. Pomiary w układach trójfazowych niesymetrycznych

Rozważmy układ trójfazowy niesymetryczny czteroprzewodowy (Z_A≠Z_B≠Z_C). Do pomiaru mocy czynnej należy użyć trzech watomierzy, których cewki prądowe włączone są na poszczególne prądy liniowe, natomiast cewki napięciowe włączone są pomiędzy daną fazę a przewód neutralny (zerowy), jak to ilustruje rys.13.14.

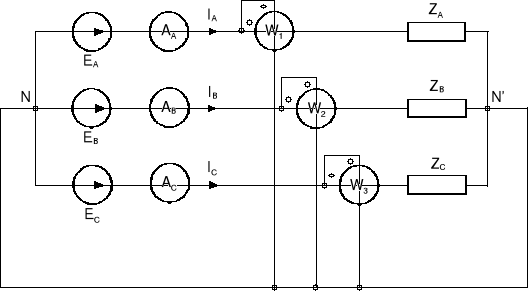
Rys.13.14. Pomiar mocy czynnej w układzie trójfazowym niesymetrycznym czteroprzewodowym

Całkowita moc czynna jest sumą mocy czynnych w poszczególnych fazach, czyli

. (13.44)
Moc pozorna

. (13.45)

Analizując wzór (13.45), można zauważyć, że aby pomierzyć moc pozorną, należy zmierzyć napięcia fazowe generatora i poszczególne prądy liniowe i wykonać działania zgodnie z wzorem (13.45).

Moc bierną zmierzymy za pomocą trzech waromierzy, spełniających rolę watomierzy włączonych tak jak pokazano na rys. 13.15, które mierzą:

Q₁ =U_BCI_Acos< (U_BC, I_A) +U_CAI_Bcos< (U_CA, I_B) +

+U_ABI_Ccos< (U_AB, I_C) . (13.46)

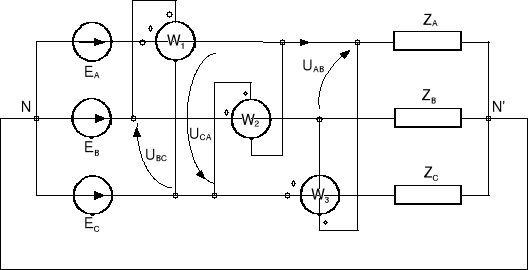
Rys.13.15. Pomiar mocy biernej w układzie trójfazowym niesymetrycznym czteroprzewodowym

Korzystając z wykresu wektorowego przedstawionego na rys.13.10, (ϕ_A ≠ ϕ_B ≠ ϕ_C) wzór (13.46) można przekształcić do postaci

, (13.47)

po dalszych przekształceniach otrzymujemy:

. (13.48)

Wielkość określona wzorem (13.48) jest ściśle powiązana z mocą bierną odbiornika, mianowicie:

, (13.49)
gdzie: Q - moc bierna odbiornika.

Rozważmy obecnie układ trójfazowy niesymetryczny trójprzewodowy przedstawiony na rys.13.16.

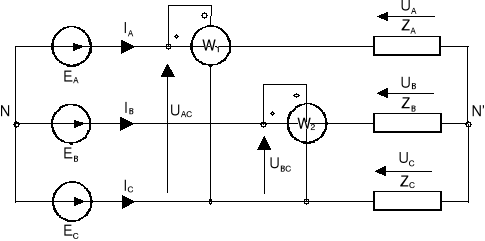
Rys.13.16. Pomiar mocy czynnej w układzie trójfazowym trójprzewodowym za pomocą dwóch watomierzy (układ Arona)

Dla układu przedstawionego na rys.13.16 moc symboliczna pobierana przez odbiornik niesymetryczny, wynosi:

. (13.50)

Dla układu trójfazowego trójprzewodowego (rys.13.16) na podstawie I prawa Kirchhoffa zachodzi związek

, jak również
,

stąd
. (13.51)

Wstawiając zależność (13.51) do wzoru (13.50) mamy

, (13.52)
gdzie:

Re{S} = P = P₁ + P₂ =U_ACI_Acos< (U_AC, I_A) +U_BCI_Bcos< (U_BC, I_B), (13.53)

Im{S} = Q = Q₁ + Q₂ =U_ACI_Asin< (U_AC, I_A) +U_BCI_Bsin< (U_BC, I_B). (13.54)

Z zależności (13.53) wynika, że do pomiaru mocy czynnej odbiornika należy użyć dwóch watomierzy włączonych w sposób przedstawiony na rys.13.16. Wykres wektorowy napięć i prądów przedstawiono na rys.13.17

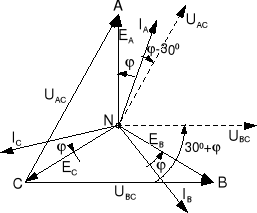
Rys.13.17. Wykres wektorowy prądów i napięć dla układu z rys.13.16

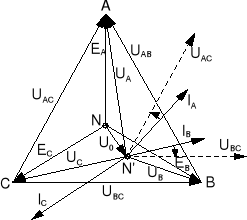
Rys.13.18. Wykres wektorowy prądów i napięć dla układu z rys.13.16 przy założeniu, że ZA=ZB=ZC

Jeżeli odbiornik jest symetryczny, to wykres wektorowy z rys.13.17 przedstawiony jest na rys.13.18 przy założeniu, że odbiornik ma charakter rezystancyjno - indukcyjny.

Na podstawie wykresu wektorowego pierwsze wyrażenie ze wzoru (13.53) ma postać

, (13.55)

natomiast drugie wyrażenie wzoru (13.53) sprowadza się do zależności

. (13.56)
Ostatecznie moc czynna odbiornika określona jest za pomocą zależności

. (13.57)

Przebiegi wskazań watomierzy P₁ i P₂ oraz ich sumy
(w jednostkach względnych, tzn. w odniesieniu do iloczynu
) w funkcji kąta fazowego φ przedstawiono na rys.13.19.

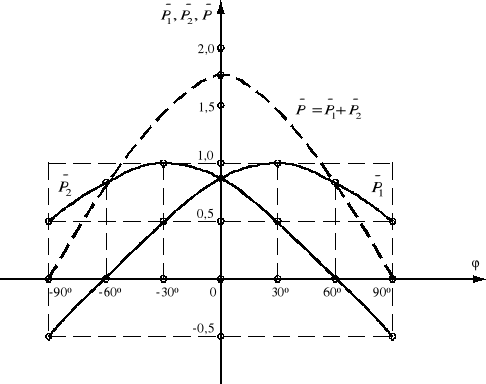
Rys.13.19. Przebiegi względnych (odniesieniu do iloczynu
) wskazań watomierzy P₁ i P₂ oraz ich sumy
w funkcji kąta fazowego φ odbiornika symetrycznego

Z rys.13.19 wynika, że mimo symetrii układu, w ogólnym przypadku wskazania watomierzy nie są jednakowe (są tylko jednakowe dla odbiornika o charakterze rezystancyjnym, tzn. dla φ = 0). Oba wskazania są dodatnie dla kątów fazowych -60^o<φ<60^o . Dla kątów -60^o<φ<-90^o oraz 60^o<φ<90^o , wskazania watomierzy mają różne znaki. Przy kącie fazowym φ=±90^o wskazania są równe co do bezwzględnej wartości, ale ich znaki są przeciwne, co daje, że
.

Różnica wskazań watomierzy określona jest wzorem

. (13.58)

Na podstawie wskazań watomierzy dla rozpatrywanego układu symetrycznego możemy wyznaczyć co do modułu kąt przesunięcia fazowego pomiędzy napięciem fazowym a prądem liniowym

, (13.59)

a stąd

. (13.59a)

Natomiast czy prąd wyprzedza napięcie fazowe, tzn. czy odbiornik ma charakter rezystancyjno-pojemnościowy, czy się spóźnia (charakter rezystancyjno-indukcyjny), (rys.13.18), należy ocenić na podstawie wskazań watomierzy P₁ lub P₂.

Moc bierna dla odbiornika symetrycznego

(13.60)

i wtedy ze wzoru (13.58) otrzymuje się:

. (13.61)

1

17

---