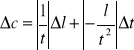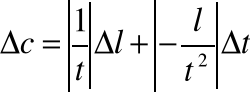
Błędy pojedynczych pomiarów liczyłem metodą różniczki zupełnej, korzystając ze wzoru:
Nr. Ćwicz. 320 |
data 18-03-1999 |
Andrzej Gessner |
WBMiZ |
Semestr: IV |
grupa : M1 |
Prowadzący: mgr Szymon Semran |
|
|
Przygotowanie: |
Wykonanie: |
ocena ostatecz.: |
TEMAT: POMIAR PRĘDKOŚCI ŚWIATŁA METODĄ IMPULSOWĄ
1. Cel ćwiczenia:
Celem ćwiczenia jest pomiar prędkości światła metodą względnego opóźnienia w czasie dwóch impulsów świetlnych przebywające różne drogi.
2. Wprowadzenie:
Każdy proces falowy charakteryzują dwie różne prędkości rozchodzenia się: prędkość fazowa i grupowa. Prędkość fazowa jest to prędkość z którą przemieszcza się w przestrzeni faza fali harmonicznej opisana równaniem
Ψ = Asin( ωt - kx)
gdzie:
A - amplituda drgań zaburzenia falowego
ω = 2Π/T - częstotliwość kątowa drgań
t - czas
k = 2Π/λ - liczba falowa
x - współrzędna stanowiąca odległość punku od źródła zaburzenia
Prędkość z jaką rozchodzi się zaburzenie falowe tak aby faza α = ωt - kx =const wynosi:
Rozchodzenie się zaburzenia falowego o dowolnym kształcie w ośrodku liniowym, w którym natężenie zaburzenia nie wpływa na jego rozchodzenie się, można przedstawić jako rezultat nałożenia się fal harmonicznych o różnych częstotliwościach ω. Istnienie dyspersji v(ω) oznacza, że różne składowe przemieszczają się z różnymi prędkościami fazowymi. Dlatego też zaburzenie wypadkowe będzie miało w różnych chwilach różne kształty Im mniejsza jest dyspersja lub im węższe jest widmo zaburzenia przy danej dyspersji, tym wolniej zmienia się kształt obwiedni podczas rozprzestrzeniania się zaburzenia. Dla takiego przedziału czasu w którym kształt obwiedni jest zachowany, można wprowadzić prędkość przemieszczania się obwiedni nazywaną prędkością grupową „u” Wewnątrz obwiedni fala rozchodzi się z pewną prędkością fazową „v”.
Zgodnie ze szczególną teorią względności przekazywanie oddziaływań fizycznych, przekazywanie dowolnych sygnałów oraz ruch ciał materialnych nie może odbywać się z prędkością większą od prędkości światła. Zjawisko dyspersji światła powoduje, że prędkość światła w ośrodku zależy od częstotliwości. Dlatego należy rozróżniać prędkość fazową:
3. Pomiary i obliczenia.
Informacje dodatkowe:
L=9,50±0,05m
Dokładność pomiarów:
Δt=0,001μs
ΔL=0,05m
Tabelka pomiarowa:
Podstawa czasu oscyloskopu [MHz] |
Czas t [μs] |
Prędkość światła c [m/s] |
Błąd Δc [m/s] |
2,0 |
0,027 |
351851852 |
14883402 |
|
0,028 |
339285714 |
13903061 |
1,9 |
0,029 |
327586207 |
13020214 |
|
0,028 |
339285714 |
13903061 |
1,8 |
0,029 |
327586207 |
13020214 |
|
0,030 |
316666667 |
12222222 |
1,7 |
0,030 |
316666667 |
12222222 |
|
0,031 |
306451613 |
11498439 |
1,6 |
0,029 |
327586207 |
13020214 |
|
0,029 |
327586207 |
13020214 |
1,5 |
0,030 |
316666667 |
12222222 |
|
0,031 |
306451613 |
11498439 |
1,4 |
0,031 |
306451613 |
11498439 |
|
0,029 |
327586207 |
13020214 |
1,3 |
0,029 |
327586207 |
13020214 |
|
0,029 |
327586207 |
13020214 |
1,2 |
0,031 |
306451613 |
11498439 |
|
0,029 |
327586207 |
13020214 |
1,1 |
0,032 |
296875000 |
10839844 |
|
0,029 |
327586207 |
13020214 |
1,0 |
0,032 |
296875000 |
10839844 |
|
0,031 |
306451613 |
11498439 |
|
Błąd statystyczny |
||
Średnia prędkość c [m/s] |
335938438 |
42864568 |
|
Rachunek błędów.
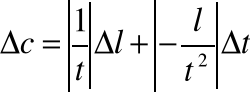
Błędy pojedynczych pomiarów liczyłem metodą różniczki zupełnej, korzystając ze wzoru:
Z uzyskanych wyników policzyłem średnią arytmetyczną, obliczyłem odchylenie standardowe i jako błąd przyjąłem jej trzykrotną wartość.
Ostateczny wynik:
c = 335 938 438 ± 42 864 568 m/s
Wnioski:
Po przeprowadzeniu obliczeń oraz rachunku błędu możemy zauważyć, że wartość światła nieco odbiega od wartości podawanej w tablicach fizycznych
(c = 299792 km/s). Stosunkowo mały błąd obliczony metodą różniczki zupełnej nie uwzględniał błędów przypadkowych ani też niedokładności wynikających z faktu, że różnica faz na oscyloskopie wyszukiwana była ręcznie, metodą oceny wzrokowej. Obliczony błąd statystyczny jest już dosyć duży. Na tak duże rozbieżności w obliczonych wartościach prędkości światła miała wpływ słaba możliwość regulowania oscyloskopu, ( zbyt duże wartości podstawy czasu ) niedokładny odczyt odległości między pikami spowodowany małą dokładnościa podziałki.