Pytania na obronę
Wielkości skalarne, wektorowe i tensorowe w fizyce.
Pojęcie układu odniesienie. Transformacja Galileusza. Układ inercjalny i nieinercjalny.
Zasada względności Einsteina. Transformacja Lorentza i jej własności. Dylatacja czasu, skrócenie długości.
Zasada zachowania w mechanice. Zderzenie sprężyste i niesprężyste.
Kinematyka i dynamika ruchu obrotowego bryły sztywnej.
Oscylator harmoniczny prosty, tłumiony i wymuszony. Zjawisko rezonansu.
Ruch punktu materialnego w polu centralnym. Prawo powszechnego ciążenia. Prawa Keplera. Wyznaczanie stałej grawitacji.
Pojęcie i opis ruchu falowego. Podstawowe zjawiska towarzyszące rozchodzeniu się fal.
Fale dźwiękowe, zakres słyszalności. Ultradźwięki.
Opis gazów, cieczy i ciał stałych z punktu widzenia kinetyczno-molekularnej teorii budowy materii.
Zasady termodynamiki. Pojęcie energii wewnętrznej, pracy i ciepła w termodynamice.
Zastosowanie I zasady termodynamiki do opisu przemian gazu doskonałego.
Przemiany fazowe. Punkt krytyczny i punkt potrójny.
Pole elektryczne, opis i podstawowe własności pól. Zachowawczy charakter pola elektrostatycznego.
Mechanizm przewodnictwa elektrycznego w ciałach stałych.
Temperaturowa zależność przewodnictwa elektrycznego przewodników i półprzewodników.
Prąd elektryczny i prawa rządzące jego przepływem.
Prąd elektryczny w cieczach, elektroliza.
Obwody prądu przemiennego. Pojęcie pojemności i indukcji elektrycznej.
Ruch cząstek naładowanych w polu elektrycznym i magnetycznym. Akceleratory cząstek.
Magnetyczne własności materii. Opis mikroskopowy i właściwości makroskopowe.
Fale elektromagnetyczne-opis. Charakterystyka widma promieniowanie elektromagnetycznego.
Oddziaływanie światła z materią.
Zjawiska świadczące o falowej naturze światła. Polaryzacja, interferencja i dyfrakcja światła.
Dualizm korpuskularno falowy. Koncepcje i zjawiska.
Budowa atomu. Model Bohra. Postulaty.
Reakcje jądrowe. Rozszczepienie, synteza jądrowa.
Rozpady promieniotwórcze. Charakterystyka promieniowania alfa, beta i gamma.
Wytwarzanie, własności i detekcja promieniowania X.
Oddziaływanie promieniowania jonizującego na organizmy żywe.
Pytania na egzamin inżynierski
1. Wielkości skalarne, wektorowe i tensorowe w fizyce.
Wielkości skalarne - wielkości, które można jednoznacznie określić za pomocą liczby i jednostki, a więc mające jedynie wartości.
Wielkościami fizycznymi, które zachowują się jak skalary są: masa, długość, czas, gęstość, energia oraz temperatura.
Skalary podlegają działaniom zwykłej algebry.
Wielkości wektorowe - wielkości, które zachowują się jak przemieszczenia. (Przemieszczenie - zmiana położenia punktu materialnego). Mają one określoną zarówno wartość, jak i kierunek oraz podlegają pewnym regułom dodawania. Wielkościami fizycznymi, które można traktować jako wektory, są: siła, prędkość, przyspieszenie, natężenie pola elektrycznego oraz indukcja magnetyczna.
Wielkości tensorowe -
Przykłady tensorów w fizyce:
Skalary: temperatura, masa, energia, gęstość, liczba cząstek;
Wektory: prędkość, siła, wektor położenia, przyspieszenie;
Tensory 2-giego rzędu:tensor pola elektromagnetycznego, tensor naprężenia w ciele stałym;
Skalary:
Temperatura- To funkcja stanu w termodynamice, która podobnie jak ciepło jest związane z sumaryczną energią kinetyczną ruchu i drgań wszystkich cząsteczek tworzących dany układ. Temperatura jest miarą „chęci” do dzielenia się ciepłem. Jeśli dwa ciała mają tę samą temperaturę, to w bezpośrednim kontakcie nie przekazują sobie ciepła, gdy zaś mają różną temperaturę, to następuje przekazywanie ciepła z ciała o wyższej temperaturze do ciała o niższej- aż do wyrównania się temperatur obu ciał.
Masa-W układzie jednostki masy SI wyrażana jest w kilogramach. Symbol stosowany przez fizyków na oznaczenia masy to: m. W teorii względności masa jest skalarem i traktowana jest niezmienniczo, gdyż Autor teorii posługiwał się konsekwentnie pojęciem masy spoczynkowej. Słuszny jest w niej związek pomiędzy energią, pędem i masą ciała:
![]()
Czasem spotyka się też pojęcie „masy relatywistycznej”.
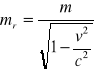
Masa relatywistyczna rośnie wraz z prędkością poruszającego się obiektu (aż do nieskończoności przy zbliżaniu się prędkości do prędkości światła).
Energia-Energia to podstawowa wielkość fizyczna, opisująca zdolność danego ciała materialnego do wykonania określonej pracy. Z punktu widzenia Termodynamiki niektóre formy energii są funkcjami stanu. Wg ogólnej teorii względności energia i masa są dwiema komplementarnymi formami występowania materii i mogą ulegać przekształceniom jednego w drugie. Energię w równaniach fizycznych zapisuje się najczęściej jako E. Jednostką energii w układzie SI jest dżul (J).
Gęstość-(masa właściwa) - masa jednostki objętości
![]()
gdzie m oznacza masę ciała, zaś V jego objętość. Jednostki: kilogram na metr sześcienny - (kg/m3) w SI.
Wektory:
Prędkość-to wektorowa wielkość fizyczna wyrażająca zmianę położenia w czasie. Prędkość w prostokątnym układzie odniesienia.
Jeżeli mamy dany wektor określający współrzędne punktu, to prędkość tego punktu obliczamy w następujący sposób:
Jednostka prędkości w układzie SI to metr na sekundę. Prędkość w ruchu jednostajnym prostoliniowym jest równa szybkości.
![]()
![]()
Prędkość w układzie odniesienia związanym z torem ruchu.
Jeżeli pokonaną przez ciało drogę oznaczymy jako s, to wartość v prędkości chwilowej ciała, będącej wektorem zawsze stycznym do toru ruchu, wyniesie:
![]()
![]()
Prędkość kątowa
Występuje w ruchu obrotowym - jest wektorem leżącym na osi obrotu i skierowanym zgodnie z regułą śruby prawoskrętnej. Jeśli współrzędną kątową ciała określa kąt alfa to wartość prędkości kątowej omega jest równa:
![]()
![]()
Jednostką prędkości kątowej w układzie SI to jeden przez sekundę.
Siła-jest wektorową miarą oddziaływań fizycznych między ciałami. Jednostką siły w układzie SI jest niuton [N]. Nazwa tej jednostki pochodzi od nazwiska wybitnego fizyka Isaaca Newtona. Siła ma wartość jednego niutona (1N) jeżeli masie 1 kilograma nadaje przyspieszenie 1 m/s2.
![]()
Przyspieszenie-wektorowa wielkość fizyczna wyrażająca zmianę prędkości w czasie. Przyspieszenie definiuje się jako pochodną prędkości po czasie. Przyspieszenie jest wielkością wektorową, gdzie wartość tego wektora jest równa wartości pochodnej prędkości względem czasu w danej chwili. Stosunek ![]()
do czasu![]()
, w jakim ten przyrost prędkości nastąpił nazywa się przyspieszeniem średnim.
Tensor 2-giego rzędu:
Pole elektromagnetyczne-pole fizyczne, za pośrednictwem którego następuje wzajemne oddziaływanie obiektów fizycznych o właściwościach elektrycznych i magnetycznych, np. naładowanych cząstek spoczywających lub będących w ruchu, dipoli magnetycznych itp.
Naprężenie-to miara gęstości powierzchniowej sił wewnętrznych występujących w ośrodku ciągłym. Jest podstawową wielkością mechaniki ośrodków ciągłych. Jednostką naprężenia jest paskal.
2. Pojęcie układu odniesienia. Transformacja Galileusza. Układ inercjalny i nie inercjalny.
Układ odniesienia - bryła sztywna, z którą ściśle związany jest układ współrzędnych wyposażony w zegar i wykorzystywany w celu określenia położenia w przestrzeni badanych brył i cząstek w różnych chwilach. Niekiedy układem odniesienia nazywa się sam chronometryczny, tzn. wyposażony w zegary, układy współrzędnych, a ciało stałe, z którym jest on sztywno związany - ciałem odniesienia. W każdym konkretnym przypadku układ odniesienia wybieramy tak, by w sposób maksymalny uprościć rozwiązanie danego zagadnienia.
Transformacja Galileusza - transformacja współrzędnych i czasu, stosowane w mechanice klasycznej przy przejściu od jednego inercjalnego układu odniesienia K(x, y, z, t) do drugiego układu K'(x', y', z', t') poruszającego się względem K ruchem postępowym ze stała prędkością V.
Rozważmy dwa układy U i U` poruszające się względem siebie ruchem jednostajnym prostoliniowym z prędkością v. Dla uproszczenia przyjmijmy, że ruch ten odbywa się równolegle do osi OX.
Rozważmy punkt P o współrzędnych (x,y,z) w układzie U. Jeżeli punkt ten pozostaje w układzie U w spoczynku to jego współrzędne w układzie U` są dane następującymi wzorami:
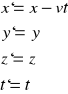
Przy czym, za rzecz oczywistą przyjmujemy, że czas w obu układach mija jednakowo.
Powyższe związki między współrzędnymi nazywamy transformacją Galileusza.
Układ inercjalny - to taki układ odniesienia, nie porusza się lub porusza się ze stałą prędkością po linii prostej (ruchem prostoliniowym jednostajnym). Innymi słowy, jego wektor prędkości nie zmienia się. Stałe pozostają jego kierunek, zwrot i wartość. W każdym układzie inercjalnym prawa fizyki są takie same i zjawiska fizyczne przebiegają w identyczny sposób. Jest to treść fundamentalnej zasady względności.
Układ nieinercia1ny to układ odniesienia, którego wektor prędkości zmienia się, czyli taki, który ma niezerowe przyspieszenie. Wektor prędkości może zmieniać tylko swoją wartość (ruch przyspieszony po linii prostej), tylko kierunek (ruch po okręgu) lub w najogólniejszym przypadku kierunek i wartość (jak na przykład przy parkowaniu samochodu kiedy to skręca się i hamuje). Charakterystyczną cechą układów inercjalnych jest występowanie w nich sił pozornych. Siła pozorna jest skierowana zawsze przeciwnie do kierunku przyspieszenia (a) układu nieinercjalnego i ma wartość (-ma), gdzie m to masa ciała, na które działa siła pozorna.
3. Zasada względności Einsteina. Transformacja Lorentza i jej właściwości. Dylatacja czasu, skrócenie długości.
Albert Einstein przyjął stałość prędkości światła jako jeden z postulatów swojej szczególnej teorii względności, tj. relatywistycznej teorii przestrzeni i czasu, obejmującej zjawiska zachodzące przy prędkościach porównywalnych z prędkością światła ![]()
.
Teorię tę sformułował w 1905 r. W pracy „O elektrodynamice ciał w ruchu” opierając ją na postulatach obowiązujących dla wszystkich układów odniesienia we względnym ruchu postępowym ze stałą prędkością ![]()
wzdłuż linii prostej (inercjalnych układach odniesienia):
I. Postulat o stałej prędkości światła. Prędkość rozchodzenia się światła jest jednakowa w każdym kierunku, we wszystkich inercjalnych układach odniesienia, niezależnie od wzajemnego ruchu źródła i obserwatora. Jest to zarazem maksymalna prędkość rozchodzenia się oddziaływań w przyrodzie.
II. Zasada względności Einsteina. Prawa przyrody mają jednakową postać we wszystkich inercjalnych układach odniesienia. Ich postać jest zatem niezmiennicza dla wszystkich obserwatorów w tych układach.
Teorię względności Einsteina nazwano szczególną teorią względności.
Transformacja Lorentza:
Układ równań transformacji Lorentza są to związki między położeniem ![]()
, ![]()
, ![]()
i czasem ![]()
zdarzenia w układzie ![]()
oraz położeniem ![]()
, ![]()
, ![]()
i czasem ![]()
tego samego zdarzenia w układzie ![]()
poruszającym się względem ![]()
ze stałą prędkością ![]()
wzdłuż osi ![]()
.
![]()
, 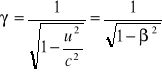
,
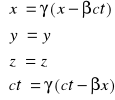
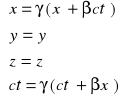
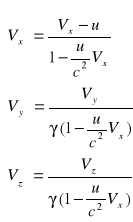
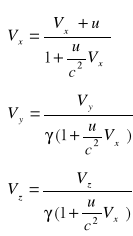
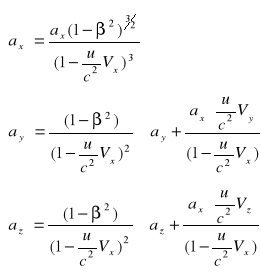
Gdy założymy, że ![]()
jest dużo mniejsze od ![]()
, czyli dla ![]()
lub ![]()
w porównaniu z ![]()
, transformacja Lorentza przechodzi w transformację Galileusza.
Dylatacja czasu:
Odstęp czasu ![]()
między dwoma zdarzeniami mierzonymi przez obserwatora R (Ruchomego) jest krótszy, niż odstęp czasu ![]()
mierzony przez obserwatora NR (nieruchomego) ![]()
![]()
, bo gdy ![]()
wtedy ![]()
Czas własny płynie wolniej! (czas własny, to czas mierzony w układzie, względem którego zegar spoczywa)
Zjawisko dylatacji czasu zostało przewidziane prze Einsteina w szczególnej teorii względności. Zjawisko to zachodzi w układach znajdujących się względem siebie w ruchu.
Kontrakcja (skrócenie) długości.
Odległość odcinka nieruchomego względem układu R mierzone z układu R ![]()
jest dłuższa, niż odległość ta mierzona z układu NR ![]()
. ![]()
![]()
, bo ![]()
jeśli ![]()
.
Odległość między dwoma punktami, mierzona w układzie, w którym te punkty spoczywają nosi nazwę długości spoczynkowej.
Dwa punkty spoczywają w NR układzie. Prowadzimy przez nie linię świata. Odległość między tymi punktami w chwili ![]()
jest mniejsza w układzie R, niż w układzie NR ![]()
.
Jeżeli te punkty spoczywają w układzie R, to odległość między nimi mierzona w chwili ![]()
jest mniejsza w układzie NR, niż w układzie R ![]()
.
Zjawisko kontrakcji długości zachodzi w układach poruszających się względem siebie.
4. Zasady zachowania w mechanice. Zderzenia sprężyste i niesprężyste.
Prawo zachowania pędu
Rozważmy układ wzajemnie oddziaływujących ciał. Najprostszymi takimi układami są na przykład dwa ciała przyciągające się według prawa powszechnego ciążenia.
Siły działające w układzie ciał dzielimy umownie na dwie grupy:
Siły wewnętrzne - siły oddziaływania pomiędzy składowymi częściami układu.
Siły zewnętrzne - siły przyłożone do składowych części układu z zewnątrz, poprzez ciała nienależące do układu. Jeśli na dany układ ciał nie działają siły zewnętrzne, to układ ten nazywamy układem izolowanym.
Prawo zachowania całkowitego pędu układu: jeżeli na układ ciał nie działają siły zewnętrzne lub wektorowa suma sił zewnętrznych równa jest zeru, to całkowity pęd układu nie zmienia się z upływem czasu:
![]()
Prawo zachowania momentu pędu
Jeżeli na dany układ mechaniczny nie działają zewnętrzne momenty obrotowe, to wektorowa suma momentów pędu części składowych tego układu nie zmienia się z upływem czasu :
![]()
Innymi słowy, wewnętrzne momenty obrotowe, działające pomiędzy częściami składowymi układu, nie mogę zmienić całkowitego momentu pędu układu. Wewnętrzne momenty obrotowe, mogą jednak spowodować zmianę energii wewnętrznej układu.
Prawo zachowania energii mechanicznej
Jeżeli na układ nie działają siły zewnętrzne lub prace sił zewnętrznych równa jest zeru, to suma energii kinetycznej i potencjalnej nie zmienia się z upływem czasu, lecz jest wielkością stałą:
![]()
Ogólne prawo zachowania energii: w układzie izolowanym suma wszystkich rodzajów energii jest wielkością nie zmieniającą się z upływem czasu.
Układ ciał nazywamy zamkniętym (odosobnionym) jeżeli można pominąć działanie sił zewnętrznych w porównaniu z działaniem sił wewnętrznych tego układu.
Pracą nazywamy iloczyn skalarny wektora siły działającej na ciało i wektora przemieszczenia tego ciała wywołanego działaniem siły.
![]()
- siła równoległa do przemieszczenia
![]()
Mocą średnią dla danego przedziału czasu ![]()
nazywamy stosunek pracy ![]()
wykonanej w tym czasie do wartości tego czasu.
![]()
Moc chwilowa
![]()
Energią kinetyczną ciała nazywamy różnicę pomiędzy jego energią całkowitą i energią spoczynkową
![]()
dla V<<c ![]()
Zderzenia sprężyste i niesprężyste
„Pęd i Ek układu kul pozostają stałe”
Rozpatrzmy zderzenia sprężyste dla kul o masach m1 i m2 oraz ich prędkości przed zderzeniami v1 i v2. Chcemy obliczyć prędkości u1 i u2 obu kul po zderzeniu. Zderzenie sprężyste charakteryzuje się tym, że energia kinetyczna przed zderzeniem równa się energii kinetycznej po zderzeniu:
![]()
Zderzające się kule traktujemy jako układ odosobniony, czyli taki, w którym działają tylko siły wewnętrzne. Obowiązuje więc zasada zachowania pędu:
![]()
Ostatecznie mamy:
![]()
![]()
Przechodzimy teraz do szczególnych przypadków zderzeń sprężystych:
Niech m1=m2, czyli kule mają jednakowe masy : u1=v1 i u2=v2 czyli kule o jednakowych masach wymieniają wzajemne swe prędkości
Zakładamy, że druga kula przed zderzeniem jest nieruchoma, czyli v2=0. Wtedy otrzymujemy
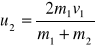
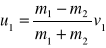
. Jeśli dodatkowo masy są równe, czyli m1=m2 to mamy: u1=0 i u2=0.Gdy druga kula ma masę znacznie większą od pierwszej i jest nieruchoma, czyli gdy m1<<m2 i v2=0 wtedy:
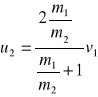
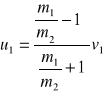
Jeżeli założymy, że ![]()
(zagadnienie odbicia od ściany), to
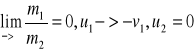
Wynika z tego, że po zderzeniu kula o dużej masie (ściana ) pozostaje nadal nieruchoma, zaś mniejsza porusza się z tą samą prędkością lecz zwróconą przeciwnie.
Jeżeli m1>>m2 a równocześnie v2=0, to :
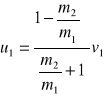
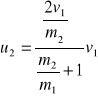
Oznacza to, że po zderzeniu kuli o bardzo dużej masie z nieruchomą kulką o masie małej, praktycznie biorąc kula duża zachowuje swą prędkość pierwotną, a kulka mała odskakuje z prędkością dwa razy większą od prędkości kuli dużej.
„Po zderzeniu suma Ek kul jest mniejsza niż przed zderzeniem, a pęd się nie zmienia”
Zderzenia niesprężyste
Ten rodzaj zderzeń rozpatrzymy na przykładzie dwóch ciał niesprężystych o masach m1 i m2 oraz o prędkościach przed zderzeniem v1i v2. Niech obie prędkości mają te same kierunki i v1 niech będzie większe od v2, czyli niech ciało pierwsze dogania drugie. Po zderzeniu, jak wiemy, następuje trwałe odkształcenie obu ciał i biegną one jako jedna bryła z prędkością u.
W czasie tego zderzenia nie działają w układzie odosobnionym siły zachowawcze, a zatem nie stosuje się zasadę zachowania energii mechanicznej. Stosuje się zasadę zachowania pędu:
![]()
Stąd prędkość wspólna obu ciał po zderzeniu równa się:
![]()
Znając energię kinetyczną obu ciał przed zderzeniem, jak również energię kinetyczną bryły utworzonej w wyniku zderzenia, można obliczyć stratę energii kinetycznej ![]()
, przekształconą na inną postać energii:
![]()
Po uwzględnieniu powyższych rozważań otrzymujemy:
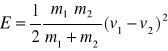
Czynnik 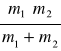
przedstawia tzw. masę zredukowaną.
5. Kinematyka i dynamika ruchu obrotowego bryły sztywnej.
Bryła sztywna - wzajemne odległości punktów nie zmieniają się podczas ruchu.
Mówimy, że ciało sztywne porusza się czystym ruchem obrotowym, jeżeli każdy punkt tego ciała porusza się po okręgu, a środki wszystkich okręgów leżą na linii prostej, zwanej osią obrotu.
Możemy dokładnie określić położenie całego wirującego ciała w naszym układzie odniesienia, jeżeli znamy położenie chociaż jednego punktu materialnego tego ciała w tym układzie.
Kinematyka ruchu obrotowego - opis ruchu punktu materialnego po okręgu w przestrzeni (dwuwymiarowej).
Średnią prędkość kątową ![]()
punktu, dla określonego przedziału czasu, definiujemy następująco: ![]()
. Natomiast chwilową prędkość kątową określamy jako graniczną wartość tego stosunku, gdy ![]()
zmierza do zera: ![]()
.
Jeżeli prędkość kątowa ciała nie jest stała, to ciało doznaje przyspieszenia kątowego: ![]()
.
Związek między liniowymi i kątowymi wielkościami kinematycznymi punktu materialnego w ruchu kołowym (postać skalarna):
Zakreślony łuk - ![]()
![]()
Prędkość liniowa - ![]()
![]()
Wartość składowej stycznej przyspieszenia - ![]()
![]()
Wartość składowej radialnej przyspieszenia - ![]()
Dynamika ruchu obrotowego.
Moment siły (dla pojedynczego punktu); ![]()
Moment pędu (--------//-------------------): ![]()
Zależność między momentem siły i momentem pędu to: ![]()
Dla układu punktów materialnych: Zmiana całkowitego momentu pędu układu punktów materialnych w jednostce czasu względem początku inercjalnego układu odniesienia jest równa sumie zewnętrznych momentów sił działających na układ.
W ciele sztywnym punkty materialne zajmują zawsze te same położenia względem siebie.
Mamy obracające się ciało. Ciało to składa się z punktów. Punkt materialny o masie ![]()
i odległości ![]()
od osi obrotu porusza się po okręgu o promieniu ![]()
z prędkością kątową ![]()
dookoła tej osi. Promień ![]()
może być różny dla różnych punktów, ale ![]()
jest stałe. Wprowadza się wielkość ![]()
. Jest to mement bezwładności ciała względem wybranej osi obrotu. Zależy on od wyboru osi obrotu, od kształtu ciała i od sposobu rozmieszczenia masy ciała.
Moment bezwładności jest opisany przy pomocy 9 współczynników. Łączą one ze sobą wektory ![]()
i ![]()
: ![]()
Twierdzenie Steinera (albo Steinera-Huygensa) - twierdzenie o osiach równoległych.: Moment bezwładności ciała sztywnego względem dowolnej osi jest równy sumie momentu bezwładności względem osi równoległej do poprzedniej i poprowadzonej przez środek masy oraz iloczynu masy ciała i kwadratu odległości obu osi: ![]()
Dynamika ruchu obrotowego - zasada zachowania momentu pędu. BĄK:
Jest sobie bąk. Bąk wiruje dookoła swojej osi symetrii. Oś takiego wirującego bąka będzie poruszać się dookoła osi pionowej, zakreślając powierzchnię stożka. Taki ruch nazywamy precesją.
Na bąk działają dwie siły: siła w punkcie podparcia działa w górę i jej moment siły względem tego punktu jest równy zeru oraz siła ciężkości ![]()
przyłożona do środka masy działa w dół i jej moment siły względem punktu podparcia wynosi ![]()
(![]()
- położenie środka masy względem punktu podparcia). Pod wpływem momentu sił działających na ciało sztywne ulega zmianie moment pędu
Prędkość kątowa precesji wynosi: ![]()
Jeszcze raz najważniejsze wzory: ![]()
, ![]()
, ![]()
,
![]()
- to równanie jest analogiem II zasady dynamiki.
6. Oscylator harmoniczny prosty, tłumiony i wymuszony. Zjawisko rezonansu.
![]()
Ruchem harmonicznym - nazywamy taki ruch periodyczny, w którym położenia ciała zmienia się w funkcji czasu sinusoidalnego.
Drgania harmoniczne wykonuje ciało o masie m, na które działa tylko siła sprężysta F=-kx ![]()
.
Ruchem harmonicznym tłumionym- nazywamy taki ruch, który odbywa się z oporami ośrodka. W takim przypadku energia maleje w czasie, zatem maleje również amplituda drgań, natomiast okres pozostaje wielkością stałą.
Oscylator harmoniczny prosty
![]()
![]()
![]()
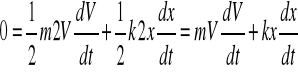
![]()
Rozwiązanie tego równania to:
V=0 (cząstka nieruchoma nie interesuje nas) ma+kx=0
![]()
![]()
![]()
przyjmujemy ![]()
i otrzymujemy ![]()
![]()
- równanie oscylatora harmonicznego prostego
Szukamy rozwiązania powyższego równania:
![]()
![]()
![]()
![]()
![]()
rozwiązanie tego równania to:
A=0 (cała funkcja jest 0) lub ![]()
lub ![]()
(niemożliwe)
Przyjmując, że:
![]()
![]()
![]()
![]()
zatem:
![]()
oraz ![]()
![]()
![]()
Wzory Eulera:
![]()
![]()
![]()
![]()
![]()
![]()
c - Amplituda
![]()
- faza drgań
![]()
- faza początkowa ruchu
![]()
Jest to ruch okresowy drgający
Oscylator harmoniczny tłumiony
Rozważmy, że dodatkową siłę, która działa na kulkę, która pod wpływem siły sprężystości przesuwała się w powietrzu drgając, działa siła oporu ze strony powietrza opisana równaniem: ![]()
gdzie: ![]()
- współczynnik drgania
![]()
- jest wprost proporcjonalna do szybkości z jaką się przesuwa ciało względem ośrodka tłumiącego
M - masa ciała
V - prędkość z jaką przesuwa się ciało względem ośrodka
Wówczas ogólne równanie ruchu jest następujące:
![]()
- minus bo siła oporu jest zawsze przeciwnie skierowana do przesuwania się cząstki, zawsze dąży one do tego, aby te cząstki zatrzymać.
![]()
![]()
![]()
![]()
równanie oscylatora harmonicznego tłumionego
Rozwiązaniem tego równania:
![]()
![]()
![]()
![]()
![]()
Jedyne rozwiązanie tego równania to:
![]()
Rozwiązanie tego równania zależy od tego jaki będzie wyróżnik takiego równania:
![]()
przyjmujemy, że ![]()
![]()
- współczynnik tłumienia
![]()
o znaku wyróżnika decyduje więc ![]()
gdy
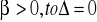
i równanie to będzie posiadało dwa pierwiastki:
![]()
![]()
a więc rozwiązanie to
![]()
- aperiodyczne
gdy
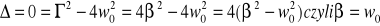
a więc ![]()
to rozwiązanie wygląda następująco:
![]()
- tłumienie krytyczne
gdy
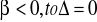
a więc nie ma rozwiązań rzeczywistych,
ale ![]()
i wtedy pierwiastki są równe ![]()
czyli w przypadku słabego tłumienia, tzn. ![]()
rozwiązaniem równania są dwie liczby zespolone:
![]()
![]()
a więc po przekształceniach rozwiązanie to będzie wyglądało następująco:
![]()
- periodyczne drganie
![]()
- logarytmiczny dekrement tłumienia
![]()
- czas relaksacji amplitudy
Oscylator harmoniczny wymuszony
Jest to oscylator, w którym obok siły harmonicznej sprężystości i obok siły oporu występuje jeszcze jedna siła, którą nazywamy siłę wymuszającą.
Ta zewnętrzna siła przykładana do układu opisana jest przy pomocy wyrażenia:
![]()
gdzie
Fo - amplituda siły wymuszającej
![]()
- częstość siły wymuszającej
![]()
![]()
![]()
i przyjmujemy ![]()
![]()
![]()
to otrzymamy:
![]()
- równanie oscylatora harmonicznego wymuszonego
7. Ruch punktu materialnego w polu centralnym. Prawo powszechnego ciążenia. Prawo Kuplera. Wyznaczanie stałej grawitacji.
Siła centralna- Siłą centralną nazywamy sił, która jest równoległa do wektora promienia wodzącego, czyli leży zawsze na prostej łączącej daną cząstkę z pewnym stałym punktem, który jest tzw. centrum siły. Może nim być np. początek układu współrzędnych. Każda siła centralna jest zachowawcza. Przykłady sił centralnych:
grawitacyjna
![]()
elektrostatyczna (coulombowska)
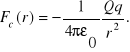
sprężysta
![]()
Wektor siły centralnej jest zawsze równoległy do wektora wodzącego, więc moment tej siły:
![]()
wynosi 0, bo sin0º = 0. Z tego natomiast wynika, że moment pędu jest stały. Ruch cząstki pod wpływem tej siły jest płaski (i odbywa się w płaszczyźnie prostopadłej do momentu pędu), więc tor ruchu jest krzywą płaską. Korzystamy z zasady zachowania energii, przy czym energia potencjalna jest funkcją odległości od centrum siły (TYLKO!!!):
![]()
Prędkość trzeba wyrazić za pomocą składowych: radialnej i transwersalnej: vr = dr / dt i vθ = rdθ / dt. Wstawiając do zasady zachowania energii mamy:
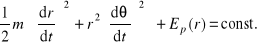
Dodatkowo trzeba skorzystać powszechnego zasady zachowania momentu pędu, gdyż to pozwoli znaleźć kierunek ruchu cząstki:
![]()
powszechnego powyższego równania trzeba wyznaczyć składową transwersalną prędkości powszechnego wstawić ją do równania na energię, a powszechnego tego można wyznaczyć składową radialną. Powinno to wyglądać tak:
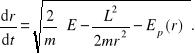
Z tego wyznaczamy dt. Potem to dt wstawiamy do zasady zachowania momentu pędu (wcześniej scałkowanej od 0 do t) i w ten sposób mamy równanie ruchu we współrzędnych biegunowych:
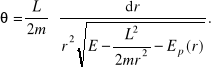
Taram. Jakby ktoś nie wiedział skąd się to wzięło, to proszę się do mnie zgłaszać (do mnie, czyli do Gosi Król). Ale to jeszcze nie koniec. Teraz trzeba rozważyć co będzie powszechnego tą energią potencjalną. Najważniejszymi siłami centralnymi powszechnego przyrodzie są siły opisane wzorem:
![]()
dla których energia potencjalna wynosi:
![]()
przy czym to χ może być np. związane z siłą grawitacji lub elektrostatyczną (patrz przykłady sił centralnych). Tą energię potencjalną wstawiamy do równania ruchu we współrzędnych biegunowych i mamy:
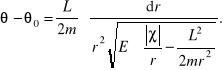
„±” pod całką oznacza odpychanie lub przyciąganie. Dalej przekształcamy to w jeszcze bardziej zawiłe wyrażenie i wprowadzamy oznaczenia:
![]()
i 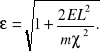
Mamy:
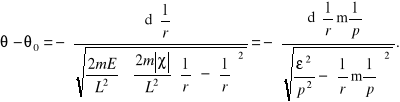
Aby uprościć drugi człon powyższego wyrażenia trzeba skorzystać powszechnego wiadomości powszechnego całkach i przypomnieć sobie, że:
![]()
Z tego widać, że ten element, w którym są epsilony, ery i pe da się doprowadzić do postaci:
![]()
z czego można wyznaczyć r:
![]()
Równanie to przedstawia krzywą stożkową; wielkość p to parametr tej krzywej, a ε - mimośród. powszechnego zależności od mimośrodu mamy:
hiperbolę, gdy ε > 1,
parabolę, gdy ε = 1,
elipsę, , gdy ε < 1,
okrąg, , gdy ε = 0.
Prawo powszechnego ciążenia- Ruch planet, satelitów, spadanie ciał na ziemię itp. świadczą o istnieniu sił wzajemnego przyciągania. Prawo powszechnego ciążenia podał Newton w 1687 roku (wyraz „powszechne” podkreśla, że wszystkie ciała posiadające masę oddziałują na siebie), formułując wzór na siłę oddziaływania grawitacyjnego:
Dwa punkty materialne o masach m1 i m2 działają na siebie siłą, która jest proporcjonalna do iloczynu tych mas i odwrotnie proporcjonalna do kwadratu odległości między nimi (a dokładnie między środkami ich mas): ![]()
lub wektorowo ![]()
.
G to skalar nazywany jest uniwersalną stałą grawitacyjną i wynosi 6,673ּ10-11 Nm2kg-1. Siła grawitacyjna między dwoma ciałami nie zależy od obecności innych ciał i właściwości otaczającej te ciała przestrzeni.
Prawa Kuplera- Pierwszym (II w.n.e), który podał znaczącą teorię na temat ruchu ciał niebieskich był Grek Ptolemeusz. Jego teoria zwana teorią geocentryczną zakładała, że Ziemia jest nieruchoma i znajduje się w środku Wszechświata, a Słońce, Księżyc, planety i gwiazdy krążą wokół niej po skomplikowanych orbitach. W XVI w. Kopernik zasugerował, że można podać prostszy opis, jeśli złoży się, że Słońce spoczywa w środku Wszechświata, a Ziemia i inne ciała niebieskie wirują wokół własnej osi i obracają się wokół niego (teoria heliocentryczna). Później dokładne obserwacje (jeszcze bez użycia lunety) poczynił Tychom Brade, a 20 lat po tym zostały one przeanalizowane przez jego asystenta - Jana Keplera. Znalazł on regularności ruchu planet i przedstawił w postaci trzech praw Keplera, które silnie poparły teorię Kopernika:
Prawo orbit. Wszystkie planety poruszają się po orbitach eliptycznych, a w jednym z ognisk elipsy znajduje się Słońce.
Prawo pól. Odcinek łączący dowolną planetę ze Słońcem (promień wodzący planety) zakreśla w równych odstępach czasu równe pola.
Prawo okresów. Kwadrat obiegu każdej planety dookoła Słońca jest proporcjonalny do sześcianu średniej odległości planety od Słońca.
Newton dzięki swojemu prawu ciążenia i zasadom dynamiki był w stanie wyprowadzić prawa Keplera.
Wyznaczanie stałej grawitacji.
Sposób 1. Polega na oznaczeniu siły oddziaływania grawitacyjnego między dwoma kulami (których znanych masach), z których jedna znajduje się na szalce wagi analitycznej (waga ma dużo szalek umieszczonych pod sobą). Na szalce umieszcza się kulę o masie kilku kilogramów i wagę równoważy się. Następnie pod dalsze szalki wagi wkłada się drugą kulę o masie kilku ton i ponownie równoważy się wagę. Ciężar dodatkowych odważników jest równy sile oddziaływania między nimi. Mierząc odległość między środkami tych mas i korzystając ze wzoru na siłę grawitacyjną można obliczyć G. Metoda ta jest jednak trudna do zrealizowania.
Sposób 2. Potrzebne są: waga analityczna, która zamiast szalek posiada kulki o masie m każda; duża, betonowa lub metalowa płyta. Pod zrównoważoną wagę - obciążoną dwoma kulkami o jednakowych masach podkłada się płytę i mierzy siłę, z jaką przyciąga ona kule. Siła ta jest równa:
![]()
,
gdzie d - gęstość materiału płyty, l - grubość płyty.
Ze względu na to, że siłą ta jest stosunkowo mała określa się ją mierząc kąt odchylenia wagi i zakładając proporcjonalność tych wielkości.
Sposób 3. Wykorzystuje się wagę skręceń. Na cienkiej nici kwarcowej z małym lusterkiem zawieszony jest pręt z dwoma kulkami o masach m. Na lusterko pada promień świetlny, odbija się od niego i pada na skalę. Podkładając z boku w okolicy mas m dodatkowe dwie masy m1 zwiększa się oddziaływanie grawitacyjne, przez co nitka kwarcowa ulegnie skręceniu. Moment sił skręcających nitkę jest proporcjonalny do jej kąta skręcenia i dodatkowo równy jest momentowi sił grawitacyjnych występujących między kulami:
![]()
gdzie r - odległość kul zawieszonych na pręcie, A - stała proporcjonalności. Siła F to:
![]()
gdzie r1 - odległość środków oddziałujących kul.
8. Pojęcie i opis ruchu falowego. Podstawowe zjawiska towarzyszące rozchodzeniu się fal.
A - amplituda fali - maksymalna wartość zaburzenia wywołanego falą w danym punkcie przestrzeni.
Długość fali - nazywamy drogę ![]()
, którą pokazuje czoło fali w czasie jednego okresu drgania jej źródła T.
![]()
v- prędkość rozchodzenia się fal
Odwrotność okresu to częstotliwość fali: (ilość pełnych drgań cząsteczek ośrodka w jednostce czasu).
![]()
Powierzchnią falową nazywamy powierzchnię utworzoną z punktów ośrodka, znajdujących się w tej samej fazie drgania. Są to zwykle punkty jednakowo odległe od źródła fali.
Czołem fali nazywamy powierzchnie falową, która w danej chwili jest najbardziej oddalona od żrodła.
Fala płaska - powierzchnie falowe są płaszczyznami.
Fala kulista - powierzchnie falowe są współśrodkowymi kulami, w środku których znajduje się źródło fali.
Równanie fali w 3 wymiarach:
Wychylenie ![]()
zależy od z,y,z,t czyli:
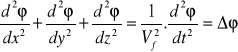
Dyfrakcja -
Polaryzacja -
Odbicie -
Załamanie -
Okres T - czas po którym cząstka zaburzonego ośrodka wykona jedno pełne drganie.
Fala (ruch falowy)- rozchodzenie się w przestrzeni zaburzenia ośrodka, przenoszące energię bez przenoszenia materii.
Fala sprężysta - rozchodzące się zaburzenie ośrodka sprężystego (gazu,cieczy)
Fala elektromagnetyczna - nie wymaga obecności żadnego ośrodka do rozprzestrzenienia się (może rozprzestrzeniać się w próżni). Polega ona na jednoczesnej propagacji pola elektrycznego i magnetycznego - jest zawsze falą poprzeczną, a konkretnie natężenie pola elektrycznego i magnetycznego są prostopadle do kierunku rozcodzenia się zaburzenia.
Fale mechaniczną nazywamy falą poprzeczną, gdy przemieszczenie cząstek ośrodka jest prostopadle do kierunku rozchodzenia się fali - Falę mechaniczną nazywamy podłużną, gdy przemieszczenie cząstek ośrodka jest równoległe do kierunku rozchodzenia się fali.
Prędkość fali nazywamy prędkość, z jaką rozchodzi się w przestrzeni zaburzenie ośrodka. Prędkość ta zależy od tego, jak szybko jedna cząsteczka ośrodka wychylona z położenia równowagi wytrąci z położenia równowagi cząsteczkę sąsiednią. To zaś jest uzależnione od sił sprężystości powstających w ośrodku i od bezwładności cząsteczek tego ośrodka.
Każde zaburzenie rozchodzące się w czasie jest opisane przy pomocy 2 współrzędnych:
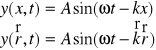
x - wychylenie tego elementu w funkcji czasu.
y - wychylenie z położenia równowagi po upływie pewnego czasu.
![]()
![]()
![]()
prędkość fazowa liczba falowa
Fale w ośrodkach sprężystych
Fale mechaniczne
Fale powstające w ośrodkach sprężystych (np. fale dźwiękowe) nazywamy falami mechanicznymi. Powstają one w wyniku wychylenia jakiegoś fragmentu ośrodka z położenia równowagi co w następstwie powoduje drgania fragmentu wokół tego położenia. Drgania te (dzięki właściwościom sprężystym ośrodka) są przekazywane na kolejne części ośrodka. Sam ośrodek nie przesuwa się, a jedynie jego elementy wykonują drgania w ograniczonych obszarach przestrzeni. Fale dobiegające do danego przedmiotu wprawiają go w ruch drgający przekazując mu energię. Można za pomocą fal przekazywać więc energię na duże odległości. Energia fal to energia kinetyczna i potencjalna cząstek ośrodka. Cechą charakterystyczną fal jest to, że przenoszą energię poprzez materię dzięki przesuwaniu się zaburzenia w materii a nie dzięki ruchowi postępowemu samej materii. Do rozchodzenia się fal mechanicznych potrzebny jest ośrodek. To właściwości sprężyste ośrodka decydują o prędkości rozchodzenia się fali.
Ze względu na kierunek drgań cząstek względem kierunku rozchodzenia się fali wyróżniamy:
- fale poprzeczne (np. lina)
- fale podłużne (np. sprężyna, głos)
Ze względu na czoło fali (powierzchnia łącząca punkty o jednakowych zaburzeniach w danej chwili) wyróżniamy:
- fale płaskie (w jednym kierunku)
- fale kuliste
Fale rozchodzące się w przestrzeni
Prędkość fazowa:
![]()
lub ![]()
gdzie: k - liczba falowa (![]()
)
Równanie ruchu harmonicznego prostego:
![]()
Równanie falowe:
![]()
Interferencja fal
Rozważmy dwie fale o równych częstotliwościach i amplitudach ale o fazach różniących się o ϕ. Równania tych fal są następujące ![]()
![]()
. Znajdźmy teraz falę wypadkową (zasada superpozycji) jako sumę ![]()
. Korzystając ze wzoru na sumę sinusów otrzymujemy:
![]()
co jest równaniem fali sinusoidalnej o amplitudzie ![]()
. Dla ![]()
fale spotykają się zgodnie w fazie (wzmacniają się), a dla ![]()
wygaszają się.
Fale stojące
Rozważmy teraz dwa ciągi falowe biegnące w przeciwnych kierunkach tzn. ![]()
![]()
np. falę padającą i odbitą. Falę wypadkową można zapisać jako: ![]()
Jest to równanie fali stojącej. Zauważmy, że cząstki drgają ruchem harmonicznym prostym. Cząstki mają tę samą częstość ale różną amplitudę zależną od położenia cząstki x. Punkty kx = π/2, 3π/2, 5π/2, itd. czyli x = λ/4, 3λ/4, 5λ/4 itd. mające maksymalną amplitudę nazywamy strzałkami a punkty kx = π, 2π, 3π itd. czyli x = λ/2, λ, 3λ/2 itd. mające zerową amplitudę nazywamy węzłami. Zwróćmy uwagę na jeszcze jedną istotną różnicę. Energia nie jest przenoszona wzdłuż sznura bo nie może ona przepłynąć przez węzły, jest na stałe zmagazynowana w poszczególnych elementach sznura.
Układy drgające
Jeżeli struna zamocowana na obu końcach zostanie najpierw wygięta a następnie puszczona, to wzdłuż struny rozchodzą się drgania poprzeczne. Zaburzenia te odbijają się od zamocowanych końców i w wyniku interferencji powstaje fala stojąca. Zwróćmy uwagę, że drgania struny wytwarzają w otaczającym strunę powietrzu dźwiękowe fale podłużne (fale akustyczne). Ponieważ jedynym warunkiem, jaki musi być spełniony, jest nieruchomość obu końców struny, czyli istnienie węzłów fali stojącej na tych końcach, to mogą powstać w tej strunie fale stojące o różnej długości. Pierwsze cztery rodzaje drgań jakie powstają w strunie o długości L zamocowanej na końcach są pokazane na rysunku poniżej. Takie fale stojące nazywamy rezonansami. Widzimy, że długości fal spełniają związek ![]()
Możliwe jest obliczenie częstotliwości rezonansów:
![]()
Najniższą częstość nazywamy częstością podstawową a pozostałe wyższymi harmonicznymi czyli alikwotami. Zazwyczaj w drganiach występują, oprócz drgania podstawowego, również drgania harmoniczne, a dźwięki jakie odbieramy są wynikiem nakładania się tych drgań. O barwie instrumentu decyduje właśnie to ile alikwotów jest zawarte w dźwięku i jakie są ich natężenia. Przykładowo, drganie wypadkowe struny będące złożeniem tonu podstawowego (n = 1) i wyższych harmonicznych (n = 3, 5, 7) o różnych amplitudach jest pokazane na rysunku poniżej.
Zwróćmy uwagę, że wypadkowe drganie (chociaż okresowe) nie jest harmoniczne (nie daje się opisać funkcją sinus lub cosinus).
Dudnienia - modulacja amplitudy
Drgania wypadkowe można uważać za drgania o częstości:
![]()
która jest średnią dwóch fal, i o amplitudzie zmieniającej się w czasie z częstością:
![]()
Jeżeli częstotliwości v1 i v2 są bliskie siebie to amplituda zmienia się powoli. Mówimy, że mamy do czynienia z modulacją amplitudy AM (stosowana np. w odbiornikach radiowych). Dla fal dźwiękowych AM przejawia się jako zmiana głośności nazywana dudnieniami (rysunek).
Zjawisko Dopplera
Austriak, Christian Doppler w pracy z 1842r. zwrócił uwagę, że barwa świecącego ciała (częstotliwość) musi się zmieniać z powodu ruchu względnego obserwatora lub źródła. Zjawisko Dopplera występuje dla wszystkich fal.
![]()
gdzie: v' - częstość odbierana przez obserwatora, v - częstość źródła, V - prędkość fali, Vo - prędkość obserwatora, Vz - prędkość źródła. Znaki w liczniku i mianowniku odpowiadają zbliżaniu się, znaki przeciwne do nich oddalaniu się obserwatora i źródła.
9. Fale dźwiękowe, zakres słyszalności. Ultradźwięki.
Ucho ludzkie jest w stanie rejestrować dźwięki o częstotliwości od 16 do 20000 Hz i wartości natężenia do 120 dB.
Częstotliwość docierającej do nas fali akustycznej daje odczucie wysokości dźwięku, a ciśnienie akustyczne - głośności. Wrażenie barwy zależne jest od widma częstotliwości przebiegów złożonych (ilości składowych harmonicznych w dźwięku). Między wartością ciśnienia akustycznego wywołującego wrażenie słuchowe a uzyskanym wrażeniem słuchowym obowiązuje zależność logarytmiczna. W akustyce stosuje się skalę logarytmiczną określaną skalą decybelową. Ciśnienie akustyczne możemy przedstawić w takiej skali za pomocą wzrou:
![]()
gdzie:
![]()
- poziom ciśnienia akustycznego
![]()
- ciśnienie akustyczne odpowiadające progowi słyszalności
Jeśli impulsy akustyczne następują po sobie w czasie krótszym niż 0,1 sekundy to ucho ludzkie w skutek bezwładności nie jest w stanie ich rozróżnić. Człowiek jest w stanie odróżnić kierunek docierającej do niego fali akustycznej. Kierunkowość ta jest większa dla wyższych częstotliwości i wynosi ok. ![]()
.
Natężenie fali dźwiękowej możemy przedstawić za pomocą wzoru:
![]()
gdzie:
S - pole powierzchni na które pada fala dźwiękowa
P - moc dźwięku
Ale ucho ludzkie logarytmuje natężenie słyszalnego dźwięku dlatego poziom słyszalnego dźwięku możemy przedstawić tak jak we wzorze 1 w dB:
![]()
I0 - natężenia dźwięku dla progu słyszalności (10-12W/m2)
Człowiek nie słyszy wszystkich częstotliwości na tym samym poziomie. Gorzej słyszalne są dźwięki wyższe i niższe. Najlepiej słyszalne są częstotliwości na poziomie ok. 3,5 kHz. Spowodowane jest to długością przewodu słuchowego, która odpowiada połowie długości fali dla 3,5 kHz i powstanie w nim rezonansu. Dlatego po analizie statystycznej wielu audiogramów wprowadzono jednostkę głośności zwaną fonem. Zależność tą przedstawia wykres krzywych izofonicznych.
Ultradźwięki
Ultradźwiękami (naddźwiękami) nazywamy fale sprężyste wytwarzane powyżej częstotliwości 20kHz (tj. umownie przyjęta górna granica słyszalności) mogą być rejestrowane (odbierane) różnymi urządzeniami, ale nie są już rejestrowane przez ucho ludzkie. Obejmują one fale o częstotliwości aż do 1GHz.
Ultradźwięki znajdują różnorodne zastosowanie w badaniach własności mechanicznych i struktury ciał. Wykorzystuje się przy tym fakt, że zmiana stanu lub cech fizycznych ośrodka wpływa na zmianę prędkości i kierunku rozchodzenia się fali. Fale ultradźwiękowe stosuje się przede wszystkim do wykrywania niejednorodności w materiałach. Ta dziedzina nazywana jest defektoskopią ultradźwiękową; używa się w niej ultradźwięków w postaci impulsu lub w postaci fali ciągłej. W pierwszym przypadku odbicie fali od defektu struktury lub granicy ośrodków powoduje wystąpienie dodatkowego impulsu, tzw. echa, który jest zarejestrowany przez odbiornik. W drugim przypadku wskutek interferencji fali padającej i odbitej powstaje fala stojąca, którą także można wykryć. Metodami ultradźwiękowymi można wyznaczać stałe sprężystości i współczynnik lepkości różnych materiałów. Również mogą one przyspieszać i polepszać pewne procesy, np. dyfuzję, suszenie. Użycie naddźwięków umożliwia przeprowadzenie procesów technologicznych, np. obróbkę twardych i kruchych materiałów, spawanie, otrzymywanie stopów. Ultradźwięki znajdują również zastosowanie w biologii i medycynie zarówno w celach diagnostycznych, jak i leczniczych (chirurgia ultradźwiękowa).
10. Opis gazów, cieczy i ciał stałych z punktu widzenia kinetyczno - molekularnej teorii budowy materii.
11. Zasady termodynamiczne. Pojęcie energii wewnętrznej, pracy i ciepłą w termodynamice.
I zasada termodynamiki (prawo zachowania i przemiany energii, dla układu w którym energia mechaniczna nie zmienia się) - Ciepło doprowadzone do układu zostaje zużyte na zwiększenie energii wewnętrznej układu i na wykonanie przez układ pracy przeciw siłą zewnętrznym.
![]()
W - praca wykonana przez układ nad ciałami zewnętrznymi
U - energia wewnętrzna układu
Q - ciepło dostarczone układowi
II zasada termodynamiki
1. Niemożliwy jest proces, którego jedynym rezultatem jest zmiana ciepła otrzymanego ze źródła ciepła na równoważną mu pracę;
Niemożliwy jest proces, którego jedynym rezultatem jest przekazanie energii w postaci ciepła od ciała zimniejszego do ciała cieplejszego.
III zasada termodynamiki
W dowolnym procesie izotermicznym przebiegającym w temperaturze zera bezwzględnego zmiana entropii układu jest równa zeru, tzn.
![]()
niezależnie od zmiany jakich kolwiek innych parametrów stanu, (objętości, ciśnienia). Zasada ta jest inaczej nazywana zasadą Nennsta.
Zasada Nernsta rozszerzył Planc, zakładając, że w temperaturze zera bezwzględnego entropia So=0. Warunek ten jest jednak spełniony tylko w przypadku takich układów, które w temperaturze T=O k, znajduje się w stanie równowagi trwałej.
Zerowa zasada termodynamiki
Istotnie wielkość skalarna, nazywana temperaturą, która jest właściwością wszystkich układów termodynamicznych(w stanie równowagi), przy czym równość temperatur jest warunkiem koniecznym i wystarczającym równowagi termicznej.
Energia wewnętrzna
Jest to część energii układu zależna tylko od jego stanu wewnętrznego i stanowi ona sumę energii oddziaływań międzycząsteczkowych i wewnątszcząsteczkowych układu oraz energii ruchu cieplnego cząsteczek.
Jest jednym z potencjałów termodynamicznych. Według I zasady termodynamiki, energia wewnętrzna stanowi jednoznaczną funkcję stanu, którą można wyrazić przez dowolne dwa z trzech parametrów: ciśnienie, objętość i temperatura.
Składa się z:
En. Kinetyczna chaotycznego ruchu cząstek
En. Potencjalną wzajemnego oddziaływania cząstek
En. wewnątrzcząsteczkową
Praca i ciepło
Wykonanie pracy jest formą przekazania energii. Jedno ciało może przekazać energię drugiemu pod dwoma postaciami. Pierwsza z nich sprowadza się do tego, że energia uporządkowanego ruchu jednego ciała przechodzi w energię uporządkowanego ruchu drugiego ciała albo jego części. To może zachodzić przy wzajemnym działaniu ciał makroskopowych o wymiarach znacznie większych od wymiarów oddzielnych atomów lub cząsteczek. Ten rodzaj przekazywania energii w termodynamice i mechanice nazywa się pracą. Na przykład, gaz rozszerzając się w cylindrze silnika spalinowego przesuwa tłok i przekazuje mu energię w postaci pracy.
Drugą postać przekazywania energii realizuje się przy bezpośredniej wymiarze energii między bezładnie poruszającymi się cząsteczkami ciał działających wzajemnie na siebie, przy czym kosztem przekazanej ciału cząstek, czyli zwiększa się energia wewnętrzna ciała. Tę formę przekazywania energii w termodynamice nazywa się ciepłem.
Wykonanie pracy nad układem, może bezpośrednio doprowadzić do zwiększania dowolnego rodzaju energii (kinetycznej, potencjalnej, wewnętrznej) natomiast dostarczenie układowi ciepła prowadzi bezpośrednio tylko do powiększenia energii wewnętrznej.
Ciepło i praca ściśle są ze sobą związane i przechodzą jedno w drugie i w warunkach realnych towarzyszą sobie wzajemnie. Doświadczenie wykazuje, że ciepło przemienia się w pracę albo praca w ciepło zawsze w dokładnie odpowiednich ilościach, niezależnie od sposobu tej przemiany. Jedna kaloria jest równoważna 4,188 dżuli.
12. Zastosowanie I zasady termodynamicznej do opisu przemian gazu doskonałego.
Przemiany izotermiczne T=const
Prawo Bule`a - Mariotta
Między parametrami zrównania gazu doskonałego.
![]()
czyli ![]()
Iloczyn ciśnienia i objętości gazu jest wielkością stałą.
W procesie izotermicznym gęstość gazu jest wprost proporcjonalna do ciśnienia. We współrzędnych p, V wykresem przemiany izotermicznej jest hiperbola.
![]()
Praca przemiany izotermicznej gazu doskonałego
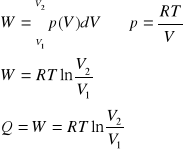
Energia wewnętrzna U gazu doskonałego podczas przemiany izotermicznej nie ulega zmianie.
Przemiana izobaryczna p=const
Prawo Gay - Lussaca
![]()
lub ![]()
![]()
Zależności pod stałym ciśnieniem objętości określonej ilości gazu doskonałego jest wprost proporcjonalna do jego temperatury bezwzględnej.
Równoważne sformułowanie tego prawa przy ogrzewaniu gazów pod stałym ciśnieniem.
Współczynnik rozszerzalności objętościowej jest stały.
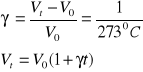
Praca przemiany p= const
![]()
gazu doskonałego
![]()
Przemiana izochoryczna V=const
Prawo Charlesa
![]()
![]()
W procesie izochorycznym ciśnienie gazu doskonałego jest wprost proporcjonalne do temperatury.
Praca przemiany
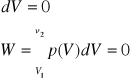
Przemiana adiabatyczna bez przepływu energii w postaci ciepła ![]()
Przy adiabatycznym sprężaniu energia wewnętrzna gazu rośnie kosztem pracy zewnętrznej.
Związek między ciśnieniem p i objętością V dla gazu doskonałego.
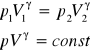
równanie Poissona
13.Przemiany fazowe. Punkt krytyczny i punkt potrójny.
Przemiany fazowe to takie procesy, w których w sposób gwałtowny (skokowy) ulegają zmianie różne właściwości ciała. Do przemian fazowych zliczamy topnienie i krzepnięcie, parowanie i skraplanie, sublimacje i resublimację
Punk krytyczny jest to punkt odpowiadający temperaturze krytycznej, w której znika różnica między cieczą i parą.
W miarę ogrzewania próbówki z cieczą jej objętość stopniowo rośnie i zaczyna ona parować. Gęstość cieczy stopniowo maleje a gęstość pary rośnie. Powierzchnia swobodna cieczy staje się coraz bardziej plaska a następnie znika. Cała próbówka wypełnia się jednolita substancją, granica miedzy cieczą i parą zanika.
Każdy gaz ma określoną temperaturę krytyczną. W temperaturze wyższej od temp. krytycznej substancje mogą występować jedynie w stanie gazowym. Poniżej temp. krytycznej można każdą substancję otrzymać w stanie ciekłym.
Punkt potrójny
Temperatura topnienia danej substancji jest to temperatura, w której obie fazy, stała i ciekła, pozostają w równowadze ze sobą. Ale jak wiadomo ta temperatura jest funkcja ciśnienia. Można zatem zrobić wykres we współrzędnych p i T, otrzymując tzw. krzywą krzepnięcia (równowagi układu ciecz-ciało stałe) rozdzielającą płaszczyznę wykresu na obszar ciała stałego i cieczy. W analogiczny sposób można wykreślić krzywą równowagi układu ciecz-gaz. Każdy punkt otrzymanej krzywej (zwanej krzywą parowania) odpowiada warunkom, w których ciecz i para danej substancji mogą istnieć w równowadze między sobą. W podobny sposób można wykreślić krzywą równowagi dla fazy stałej i gazowej (krzywa sublimacji).
Nachylenia krzywych równowagi fazowej we współrzędnych p=p(T) określa prawo Clausiusa-Clapeyrona, według którego:
![]()
,
gdzie q oznacza ciapło danej przemiany fazowej (a wiec ciepło topnienia, ciepło parowania, ciepło sublimacji); (V2 - V1) to różnica objętości tej samej masy , do której odniesione jest ciepło przemiany, w obu rozważanych fazach w temperaturze T.
Punkt potrójny jest punktem, w którym może zachodzić równowaga trzech faz.
Strzałki przedstawiają przemiany fazowe:
S - sublimacja - przejście od fazy krystalicznej do gazowej
R - resublimacja - przejście od fazy gazowej do krystalicznej
T - topnienie - przejście z fazy krystalicznej (lub amorficznej) do fazy ciekłej
K - krzepnięcie - przejście od fazy ciekłej do fazy krystalicznej lub amorficznej
Sk - skraplanie - przejście od fazy gazowej do ciekłej.
14. Pole elektryczne, opis i podstawowe własności pól. Zachowawczy charakter pola elektrostatycznego.
Wiemy, że ładunek elektryczny wywołuje w swoim otoczeniu pewne zmiany objawiające się w ten sposób, że inny ładunek wprowadzony do tego obszaru podlega działaniu sił kulombowskich ( FCoulomba= kq1q2/r2 ). Mówimy, że ładunek elektryczny wytwarza dookoła siebie pole elektryczne. Do badania pola służą ładunki próbne tak małe, by swą obecnością nie zakłócały rozkładu ładunków pozostałych. Pole elektryczne można opisywać wektorowo lub skalarnie. Przedstawienie wektorowe pola sprowadza się do wyznaczenia natężenia pola, przestawienie skalarne zaś do wyznaczenia potencjału w poszczególnych punktach pola.
1) Natężenie pola elektrycznego
Przez natężenie pola elektrycznego E w danym punkcie rozumiemy stosunek siły działającej w tym punkcie na ładunek próbny dodatni q0 do wartości tego ładunku:
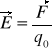
Wektor natężenia pola E ma kierunek zgodny z kierunkiem siły F.
Jeśli badane pole wytwarzane jest prze ładunek punktowy q, to uwzględniając prawo Coulomba można napisać:
![]()
Jak widać, natężenie pola wytwarzanego przez ładunek q zależy nie tylko od wartości tego ładunku i odległości r miedzy nim a punktem w którym badamy natężenia lecz także od właściwości ośrodka za pośrednictwem jego przenikalności elektrycznej ε.
W przypadku, gdy pole elektryczne wytwarzane jest przez kilka ładunków punktowych
q1, q2, …, qn natężenie pola w dowolnym punkcie obliczmy sumując wektorowo natężenia E1, E2, …, En pochodzące od poszczególnych ładunków ładunków obliczone przy założeniu, że każdy z nich jest jedynym ładunkiem wytwarzającym pole:
![]()
2) Linie sił pola elektrycznego, strumień elektryczny
Do modelowego opisu pola elektrycznego stosuje się wprowadzone przez Faradaya tzw. linie sił pola elektrycznego. Linia siły jest to linia o takim przebiegu, że styczna do niej poprowadzona w dowolnym jej punkcie wyznacza kierunek wektora natężenia pola elektrycznego w tym punkcie. Dla ładunku dodatniego wszystkie linie zaczynają się na tym ładunku i rozbiegają promieniście w przestrzeń. Układ linii dla pojedynczego ładunku ujemnego byłby radialny zbieżny: wszystkie linie z przestrzeni dochodziły by do ładunku ujemnego i na nim się kończyły. Można powiedzieć, że linia siły przedstawia tor ruchu swobodnego, pozbawionego masy, ładunku próbnego elektrycznie dodatniego, wprowadzonego do pola. Kierunek zaznaczany strzałką na linii to kierunek ruchu wymienionego ładunku. W zasadzie linie sił pola elektrycznego można by poprowadzić dowolnie gęsto, jednak wprowadzono umowę normującą gęstość linii. Przez strumień Φ linii sił pola elektrycznego - zwany też krótko strumieniem elektrycznym - przez daną powierzchnię rozumiemy liczbę linii sił przebijających te powierzchnię. Przez gęstość strumienia elektrycznego rozumiemy stosunek dΦ/dSp, przy czym dSp jest elementarną powierzchnią ustawioną prostopadle do kierunku linii pola. Według umowy gęstość strumienia elektrycznego jest równa wartości liczbowej natężenia pola elektrycznego na tej powierzchni:
![]()
Stąd elementarny strumień elektryczny przechodzący przez powierzchnię dSp równa się:
![]()
3) Prawo Gaussa
Prawo Gaussa dotyczy zależności strumienia elektrycznego przechodzącego przez dowolna zamkniętą powierzchnię do ogólnego ładunku q znajdującego się w obszarze zamkniętym tą powierzchnią:
![]()
Jak widać z otrzymanego wzoru, całkowity strumień elektryczny nie zależy od kształtu powierzchni przez którą przechodzi, a zależy od ładunku q znajdującego się wewnątrz i od przenikalności elektrycznej ośrodka.
4) Wektor indukcji elektrostatycznej
Wobec nieciągłości strumienia linii sił pola w ośrodkach niejednorodnych nie możemy w nich stosować prawa Gaussa w poznanej postaci. Można jednak wprowadzić nowy wektor związany z E, ale tak dobrany, by nie ulegał zmianie na granicy dwóch ośrodków. Taką właściwość ma wektor indukcji elektrostatycznej D zdefiniowany równaniem:
![]()
Wartość indukcji elektrostatycznej nie zależy od ośrodka.
5) Potencjał elektryczny
Przez potencjał elektryczny danego punktu rozumiemy pracę, jaką muszą wykonać siły pola, aby ładunek jednego kulomba przenieść z danego punktu do nieskończoności lub pracę jaką muszą wykonać siły zewnętrzne przy przeniesieniu ładunku jednego kulomba z nieskończoności do danego punktu.
Aby wyznaczyć różnicę potencjałów między punktami A i B znajdującymi się w polu elektrycznym, przesuwamy ładunek próbny q0 z A do B mierząc jednocześnie pracę WAB, którą w tym celu należy wykonać. Różnica potencjałów elektrycznych jest określona jako:
![]()
Zazwyczaj jako punkt A wybiera się punkt znajdujący się w dużej odległości od wszystkich ładunków, ściślej biorąc w nieskończoności, i wówczas przyjmuje się, że potencjał elektryczny VA w tym punkcie równa się zero. Pozwala nam to na określenie potencjału elektrycznego w konkretnym punkcie:
![]()
Potencjał danego punktu jest wielkością skalarną, która może przyjmować wartości dodatnie jak i ujemne. Różnica potencjałów jest niezależna od drogi dla dowolnych dwóch punktów w dowolnym polu elektrostatycznym.
Zbiór punktów, w których potencjał elektryczny jest jednakowy, nazywamy powierzchnia ekwipotencjalną.
Praca przenoszenia ładunku w polu elektrycznym jest niezależna od kształtu drogi przenoszenia, przez co potencjał danego punktu pola jest jednoznacznie określony.
6) Praca przenoszenia ładunków w polu
Ładunek q0 wprowadzony do pola elektrycznego podlega działaniu sił elektrycznych. W przypadku ładunku swobodnego siły pola wykonują pracę przesuwając go wzdłuż linii siły. Praca dW wykonana w nieskończenie małym elemencie drogi ds wynosi:
![]()
Praca przenoszenia ładunków w polu elektrycznym jest niezależna od kształtu drogi, lecz tylko od jej punktu początkowego i końcowego. Mówimy zatem, że siły pola elektrostatycznego są siłami zachowawczymi.
Ponadto praca przenoszenia ładunku w polu elektrostatycznym po dowolnej krzywej zamkniętej jest równa zeru. Takie pole nazywamy polem bezwirowym.
15. Mechanizm przewodnictwa elektrycznego w ciałach stałych.
Atomy pierwiastków tworzących wiązania metaliczne charakteryzują się tym, że ich zewnętrzne elektrony walencyjne są przyciągane przez jądro znacznie słabiej niż u atomów pierwiastków niemetalicznych. Przy kondensacji par metali elektrony walencyjne tracą wieź z oddzielnymi atomami. i stają się wspólne dla całego kryształu wiążąc ze sobą rdzenie atomowe. Uwspólnienie elektronów walencyjnych jest nowym typem wiązania chemicznego wywołującego występowanie wielu cech charakterystycznych dla metali, przede wszystkim ich dobrego przewodnictwa elektrycznego i cieplnego. Podobieństwo między wiązaniem atomowym a metalicznym polega na tym, że w obu typach wiązań występuje uwspólnienie elektronów wiązanie atomowe łączy z sobą jedynie najbliższe atomy a uwspólnione elektrony tworzące te wiązania są zlokalizowane w pobliżu tych atomów natomiast w przypadku wiązania metalicznego mamy do czynienia z delokalizacją tych elektronów. Z tego powodu większość kryształów atomowych charakteryzuje się dużą kruchością, a kryształów metalicznych dużą plastycznością. Elektronowa teoria ciała stałego zajmuje się opisem zachowania się w krysztale rdzeni atomowych tworzących sieć przestrzenną oraz elektronów walencyjnych uczestniczących w tworzeniu się wiązań chemicznych pomiędzy tymi rdzeniami. Najsłabiej związane elektrony walencyjne mogą już pod działaniem niezbyt dużych sił wyzwolić ze strefy oddziaływania danego rdzenia i wędrować po krysztale. Takie elektrony odpowiedzialne są za wiele specyficznych właściwości ciał stałych. . np. przewodnictwo elektryczne. Przewodnictwo elektryczne w ciałach stałych. polega na ruchu nośników ładunków elektrycznych, np. elektronów; wartość przewodnictwa zależy więc od liczby tych nośników w ciałach stałych. Pod tym względem ciała stałe dzielą się na 3 grupy: przewodniki (metale), półprzewodniki i dielektryki (izolatory). Wraz ze wzrostem temp. przewodnictwo elektryczne przewodników (metali) maleje, natomiast w temperaturach bliskich 0°K staje się ono bardzo duże (nadprzewodnictwo). Przewodnictwo półprzewodników i dielektryków rośnie ze wzrostem temp.; w temp. niskich pół-przewodniki, praktycznie biorąc, nie przewodzą prądu elektrycznego.
Próbę wyjaśnienia istoty przewodnictwa metali podjął 1900 P. Drude, wychodząc z założenia, że w metalach liczba swobodnych elektronów jest bardzo duża ; z prac tych wywodzi się tzw. elektronowa teoria metali. W powstała ogólniejsza, kwantowo-mechaniczna teoria, tzw. teoria pasmowa, która wyjaśniła m.in. istotę przewodnictwa elektrycznego ciał stałych.. W swobodnych atomach elektrony powłoki atomowej znajdują się w określonych stanach (poziomach) energetycznych opisywanych liczbami kwantowymi; stany te oddzielone są strefami energii wzbronionej. Zgodnie z Pauliego zasadą wykluczenia poszczególny stan mogą zajmować 2 elektrony o przeciwnie skierowanych spinach. Każdy elektron powłoki może być przeniesiony ze swego stanu podstawowego do stanu wyższej energii stanu wzbudzonego (jeżeli stan ten jest nie obsadzony), np. w wyniku pochłonięcia kwantu energii. Ponieważ sieć składa się z identycznych, rozmieszczonych w sposób periodyczny atomów, zakłada się, że nierozróżnalność atomów rozciąga się na elektrony ich powłok. Wszystkie elektrony należą więc do całego kryształu, traktowanego jako jedna wielka cząsteczka. Oznacza to, że każdy dozwolony poziom energetyczny swobodnego atomu musi być teraz zastąpiony przez pasmo b. bliskich siebie dozwolonych poziomów energetycznych, gdyż elektrony dostarczone do wspólnoty przez poszczególne atomy nie mogą obsadzać tego samego stanu kwantowego. W krysztale zawierającym N atomów istnieje więc tyleż stanów w każdym dozwolonym paśmie energii. Pasmo obsadzone przez elektrony walencyjne nosi nazwę pasma podstawowego lub walencyjnego, najbliższe dozwolone pasmo puste odpowiednik stanów wzbudzonych w atomach swobodnych- nazywa się pasmem przewodnictwa. W temp. 0°K elektrony obsadzają parami najniższe stany energii w paśmie; jeżeli atomy mają po jednym elektronie walencyjnym (np. atomy metali alkalicznych), to pasmo podstawowe jest tylko w połowie wypełnione. Obecność nie obsadzonych stanów w tym paśmie umożliwia ruch elektronów wewnątrz pasma, a więc decyduje o przewodnictwie elektrycznym Liczba elektronów przewodzących prąd elektr. (tzw. elektronów przewodnictwa) jest tego samego rzędu co liczba atomów w sieci krystalicznej (tzn.1022 na cm3) .Z nierozróżnialności elektronów w paśmie dozwolonej energii wynika, że się nie zmieni stan energetyczny kryształu, jeśli 2 elektrony zamienią swoje miejsca i stany; stan wzbudzenia energetycznego w dowolnym węźle sieci krystalicznej może się zatem przenosić na wszystkie równoważne węzły sieci; w ten sposób interpretuje się rozchodzenie się wzbudzeń optycznych i elektronów w krysztale. Gdy pasmo walencyjne i pasmo przewodnictwa zachodzą na siebie, tzn., gdy nie oddziela ich strefa energii wzbronionej, ciał stałych. jest przewodnikiem (np. metale).
16. Temperaturowa zależność przewodnictwa elektrycznego przewodników i półprzewodników.
17.Prąd elektryczny i prawa rządzące jego przepływem.
Prąd elektryczny - uporządkowany (skierowany) ruch ładunków elektrycznych.
Nośnikami prądu elektrycznego mogą być elektrony, jony bądź dziury, czyli puste miejsca po elektronach. W metalach swobodnie przemieszczają się jedynie elektrony, dlatego prąd elektryczny w metalach jest ruchem elektronów przewodnictwa. W półprzewodnikach nośnikami prądu są elektrony i dziury. W rozrzedzonych gazach nośnikami ładunku elektrycznego są elektrony i jony.
Natężenie prądu elektrycznego I definiuje się jako stosunek ładunku elektrycznego q, który przepływa przez poprzeczny przekrój przewodnika do czasu t przepływu tego ładunku:
Jednostką natężenia prądu elektrycznego w układzie SI jest amper [A]. Bardzo często używa się tego wyrażenia zamiennie z natężeniem prądu.
Prawa związane z prądem elektrycznym: pierwsze prawo Kirchhoffa, drugie prawo Kirchhoffa, prawo Ohma.
Bilansów prądów w węźle obwodu elektrycznego prądu stałego
Dla każdego węzła obwodu elektrycznego suma algebraiczna wartości chwilowych prądów jest równa zeru.
∑ |
Iα = 0 |
α = 1,2,... |
|
Przyjmuje się konwencję, że prądy zwrócone do węzła mają znak (+), zaś prądy ze zwrotem od węzła mają znak (-), np.:
I1 + I2 + I3 − I4 − I5 − I6 = 0
Zasada bilansu prądów
Dla każdego węzła obwodu elektrycznego suma prądów dopływających do węzła jest równa sumie prądów odpływających od węzła, np.:
I1 + I2 + I3 = I4 + I5 + I6
Ściślej
Całka po powierzchni zamkniętej gęstości prądu jest równa zero:
(Całka podwójna jest po powierzchni zamkniętej - takie kółeczko oplatające obie całki.)
J - gęstość prądu (np. w A/metr2
S - powierzchnia m2
Podstawy teoretyczne
Pierwsze prawo Kirchhoffa jest prostą konsekwencją zasady zachowania ładunku oraz stwierdzeniu, że w węźle praktycznie nie może gromadzić się ładunek.
Drugie prawo Kirchhoffa - zwane również Prawem napięciowym, dotyczy bilansu napięć w zamkniętym obwodzie elektrycznym.
Treść prawa:
Suma wartości chwilowych sił elektromotorycznych występujących w obwodzie zamkniętym równa jest sumie wartości chwilowych napięć elektrycznych na elementach pasywnych tego obwodu:
∑ |
ek = |
∑ |
ul |
k |
|
l |
|
Gdzie ek to wartość chwilowa sem k-tego źródła; ul - napięcie na l-tym elemencie oczka.
Prawo to występuje również w prostszej wersji:
Suma napięć źródłowych w dowolnym obwodzie zamkniętym prądu stałego równa jest sumie napięć na odbiornikach.
przykładowy obwód zamknięty
Dla poniższego obwodu zamkniętego z prawa napięciowego wynikają następujące własności:
Inny przykład obwodu zamkniętego
U1 = I * R1
U2 = I * R2
E = U1 + U2
E = I(R1 + R2)
Jeszcze inna wersja tego prawa:
Suma sił elektromotorycznych (Ε) i spadków napięć w obwodzie zamkniętym jest równa zero.
Matematycznie: napięcie obliczone po krzywej zamkniętej jest równe zero:
przy czym
jest wektorem natężenia pola elektrostatycznego.
Prawo Ohma - natężenie prądu stałego I jest proporcjonalne do całkowitej siły elektromotorycznej w obwodzie zamkniętym lub do różnicy potencjałów (napięcia elektrycznego) między końcami części obwodu niezawierającej źródeł siły elektromotorycznej:
Współczynnik proporcjonalności w tej relacji nazywany jest konduktancją, oznaczaną przez G.
I = GU
Odwrotność konduktancji nazywamy oporem elektrycznym przewodnika:
Zatem wzór przyjmuje najczęściej używaną postać:
Prawidłowość tę odkrył w 1827 roku niemiecki fizyk, profesor politechniki w Norymberdze i uniwersytetu w Monachium Georg Simon Ohm (1787-1854).
Jeśli jakiekolwiek dwie wartości są znane, trzecią można łatwo obliczyć. Na przykład, jeśli różnica potencjałów 110 V wysyła przez przewodnik prąd 10 A, opór przewodu będzie wynosił R=U/I = 110/10 = 11 omów. Jeśli U=110 V i R=11 omów, wtedy I=U/R = 110/11 = 10 A.
Jeśli w niniejszym przykładzie napięcie zostałoby podniesione do 220 V, opór nadal miałby wartość 11 omów. Jednak prąd I zostanie podwojony, bo I=U/R = 220/11 = 20 A.
Prawo to nie jest ściśle spełnione dla większości materiałów. Materiały, które się do niego stosują, nazywamy przewodnikami omowymi lub "przewodnikami liniowymi" - w odróżnieniu od przewodników nieliniowych, w których opór jest funkcją natężenia płynącego przez nie prądu. Aby warunek liniowości był spełniony, muszą jednak być zachowane stałe warunki fizyczne (np. temperatura). Ze wszystkich materiałów przewodzących prawo Ohma najdokładniej jest spełnione w przypadku metali.
Istnieją jeszcze dwie inne postacie prawa Ohma:
różniczkowe prawo Ohma:
lokalne prawo Ohma:
gdzie
- gęstość prądu
- tensor przewodnictwa elektrycznego
- natężenie pola elektrycznego
18.Prąd elektryczny w cieczach, elektroliza.
Elektroliza - proces rozkładu elektrolitu, mający miejsce podczas przepływu prądu elektrycznego przez zdysocjowany elektrolit. Elektrolit ten może być zdysocjowany rozpuszczeniem w rozpuszczalniku, lub roztopieniem pod wpływem temperatury (wtedy mamy doczynienia z termoelektrolizą).
Proces elektrolizy polega na wędrówce jonów do elektrod: ujemnych anionów do dodatniej anody, a dodatnich kationów do ujemnej katody, czego efektem są dwie reakcje chemiczne odbywające się równolegle i bilansujące się: w otoczeniu anody jest to reakcja utleniania, a w otoczeniu katody reakcja redukcji.
Zjawisko elektrolizy zostało opisane ilościowo w dwóch prawach elektrolizy Faradaya.
19. Obwody prądu przemiennego. Pojecie pojemności i indukcyjności elektrycznej.
Obwody prądu zmiennego:
Dwójnik szeregowy RL
RL=w L
Dwójnik szeregowy RC
![]()
3. Dwójnik szeregowy RLC
4. Dwójnik równoległy RLC
Pojemność elektryczna - wielkość charakteryzująca zdolność przewodnika do gromadzenia ładunku; pojemność elektryczna przewodnika jest równa stosunkowi ładunku c zgromadzonego na przewodniku do potencjału v wywołanego obecnością tego ładunku. Jednostką jest Farad [F] pigulka 194
![]()
Indukcja elektryczna - wielkość charakteryzująca pole elektryczne wewnątrz dielektryka
![]()
[H]
Aby zapewnić prawidłową pracę stacji elektroenergetycznych i ciągłość dostawy energii, należy zadbać o niezawodność zasilania urządzeń pomocniczych i obwodów wtórnych stacji (obwody sterowania, zabezpieczeń i sygnalizacji). Wymienione obwody i urządzenia mogą być zasilane prądem przemiennym lub stałym.
Prądem przemiennym są zasilane przede wszystkim:
· obwody oświetlenia stacji;
· obwody ogrzewania stacji;
· napędy przełączników zaczepów transformatorów;
· prostowniki do zasilania obwodów prądu stałego i ładowania baterii akumulatorów;
· sprężarki - w przypadku stosowania aparatów o napędzie pneumatycznym (sprężone powietrze);
· napędy silnikowe łączników;
· obwody łączności;
· inne urządzenia, np. wentylatory.
Ponieważ urządzenia te są zasilane niskim napięciem, to najczęściej konieczne jest zainstalowanie specjalnych transformatorów i rozdzielnic potrzeb własnych. Zapotrzebowanie mocy na potrzeby własne, w zależności od rozmiarów stacji i rodzaju aparatów, wynosi od kilkunastu do kilkuset kilowatów.
W stacjach transformatorowych na niskie napięcie zasilanie potrzeb własnych może być bezpośrednie (z szyn rozdzielnic nn). Stacje średniego napięcia mają najczęściej jeden transformator potrzeb własnych, natomiast stacje wyższego napięcia - dwa.
Sposób przyłączenia transformatorów potrzeb własnych zależy od tego, czy stacja ma baterię akumulatorów. Jeżeli bateria akumulatorów jest zainstalowana, to transformatory potrzeb własnych przyłącza się do szyn zbiorczych średniego napięcia. Jeżeli brak jest baterii akumulatorów, to transformatory potrzeb własnych przyłącza się bezpośrednio do dolnej strony transformatorów głównych, co umożliwia zasilanie koniecznych urządzeń i obwodów nawet w czasie wyłączenia szyn zbiorczych średniego napięcia.
W stacjach o napięciu 220/110 kV lub 400/110 kV transformatory potrzeb własnych przyłącza się często do uzwojenia dodatkowego (10¸30 kV) autotransformatora. Ponieważ w tym miejscu występuje z reguły duża wartość mocy zwarciowej, przyłącza się transformatory albo bezpośrednio, albo przez dławik zwarciowy umożliwiający zmniejszenie mocy wyłączalnej wyłącznika (ten ostatni sposób jest obecnie zaniechany).
Rozdzielnice potrzeb własnych mają z reguły szyny sekcjonowane,
a w szczególnie ważnych stacjach (głównie o napięciu 220 i 400 kV) stosuje się również trzy transformatory do ich zasilania (jeden w rezerwie jawnej). Rezerwa jawna polega na utrzymywaniu pod napięciem dodatkowego urządzenia (transformatora), które włącza się pod obciążenie w razie awarii któregoś z urządzeń pracujących. Drugim rodzajem rezerwy jest rezerwa utajona, przez którą rozumie się moc, którą można obciążyć pracujące urządzenia (przedtem niedociążone).
Dla zwiększenia pewności zasilania rozdzielni potrzeb własnych wykorzystuje się nieraz niezależną sieć miejską lub przemysłową średniego napięcia. Ponadto zasilanie rezerwowe może stanowić również prądnica napędzana silnikiem spalinowym. Obwody zasilające szyny rozdzielnic potrzeb własnych są ze sobą związane automatyką SZR (samoczynne załączenie rezerwy) w celu zapewnienia ciągłości zasilania.
Odbiorniki są zasilane z rozdzielni potrzeb własnych w różny sposób. Silniki napędu łączników są zasilane zazwyczaj pierścieniowo.
W rozdzielnicach napowietrznych kable dochodzą wówczas do poszczególnych szaf kablowych umieszczonych w pobliżu łączników. Oświetlenie jest zasilane najczęściej z osobnej podrozdzielnicy. Każdą lampę zabezpiecza się oddzielnym bezpiecznikiem. Część lamp mająca zasilanie
z baterii akumulatorów stanowi oświetlenie awaryjne.
20.Ruch cząstek naładowanych w polu elektrycznym i magnetycznym. Akcelatory cząstek.
W polu elektrycznym
W przypadku stałego i jednorodnego w przestrzeni natężenia pola elektrycznego ![]()
oraz zerowego pola magnetycznego o indukcji ![]()
, równanie ruchu cząstki uprości się i przyjmie postać:
![]()
lub dla przypadku nie relatywistycznego ruchu cząstki:
![]()
Całkując to równanie dla prędkości początkowej równej ![]()
zależność prędkości ruchu cząstki od czasu wyrazi się relacją
![]()
Uwzględniając, że dla pola ![]()
![]()
![]()
Z równania na prędkość cząstki otrzymuje się wyrażenie na zmianę jej drogi w czasie w postaci
![]()
gdzie x0 jest początkową wartością współrzędnej położenia cząstki. Energia kinetyczna cząstki w tym przypadku wynosi:
![]()
lub kiedy V0=0
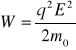
W przypadku jonów o masie mi oraz elektronów o masie mc, przy równych wartościach ładunków qi=qc kiedy siły działające na cząstki są równe lecz przeciwne skierowane Fi=-Fc dla przypadku prędkości początkowej V0=0 i po upływie czasu t energię elektronu w stosunku do energii jonu wyraża relacja Wc>>Wi. Ta różnica w energii wynika ze stosunku mas obu cząstek gdzie
![]()
Relacje prędkości cząstek oraz ich energii mają postać, odpowiednio dla jonu i elektronu
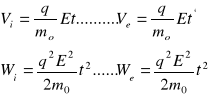
Korzystając z powyższych wyrażeń można pokazać, że
![]()
![]()
W rozważanym przypadku po upływie czasu t, jak wynika z powyższych relacji, elektron uzyska większą prędkość niż jon czyli Ve będzie > od Vi. W realnych warunkach jednak cząstka ulega zderzeniom. Przy kreślonej wartości częstotliwości tych zderzeń V prędkość cząstki stabilizuje się i cząstka nie porusza się już ruchem przyśpieszonym, który odbywa się dopóty dopóki ![]()
cząstka uzyskuje stała średnią prędkość równą
![]()
![]()
a zmianę jej położenia w czasie opisuje równanie
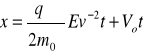
Energia kinetyczna cząstki w przypadku kiedy V0=0 jest stała i wynosi
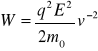
Ten sam efekt uzyska się w ośrodku bez zderzeniowym w przypadku, kiedy cząstka będzie emitowała qwanty promieniowania z częstotliwością emisji v przekazujące jej w każdym akcie emisji swój pęd. W tym przypadku pęd cząstki odrzutu jest równy pędowi emitowanego kwantu i wynosi ![]()
jest energią emitowanego kwantu. Uzyskana przez cząstkę energia kinetyczna odrzutu jest związana z pędem cząstki odrzutu zależnością
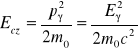
W przypadku jeżeli mamy do czynienia z sytuacją kiedy pęd odrzutu jest przejmowany przez cały ośrodek a nie pojedynczą cząstkę mamy do czynienia ze zjawiskiem bezodrzutowej emisji kwantów. Ruch cząstki w rozważanych przypadkach będzie odbywał się wzdłuż linii zmodulowanej drobnoskalową strukturą wynikającą z występowania zderzeń i emisji qwantów promieniowania. Inną interpretacją omawianego zjawiska prowadzącą do analogicznych do przedstawionych wyżej wniosków jest przyjęcie założenia, że w procesie zderzeń zachodzi modulacja amplitudy prędkości zgodnej z relacją
![]()
Gdzie
![]()
Jest przyspieszenie cząstki.
W polu magnetycznym
Rozpatrzymy teraz ruch cząstki naładowanej w obecności stałego w czasie i jednorodnego w przestrzeni pola magnetyczneo B=const oraz zerowego pola elektrycznego E=0. Relatywistyczne równanie ruchu cząstki w tym przypadku zredukuje się do postaci
![]()
Przyjmując, że prędkość cząstki można przedstawić za pomocą składowej równoległej i prostopadłej do wektora natężenia pola magnetycznego B.
![]()
Oraz uwzględniając, że pole magnetyczne nie ma wpływu na składową równoległą prędkości i dla tej składowej spełniona jest relacja
![]()
Równanie ruchu może być przedstawione w postaci układu dwóch równań dla składowej prędkości równoległej i prostopadłej do wektora B.
![]()
![]()
W rozważanym przypadku pole magnetyczne nie wykonuje pracy nad cząstką, której została nadana pewna prędkość początkowa. Pole to jedynie wpływa na zmianę trajektorii cząstki, której energia w rozważanych bezstratnych warunkach ruchu pozostaje stała. Stąd równanie zachowania energii dla tego przypadku ma postać
![]()
Przyjmując, że
![]()
Czyli, że wektor pola magnetycznego ma tylko składową wzdłużną a także, że
![]()
Oraz, że
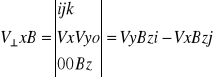
I przyrównując wyrażenia stojące przy wersorach po prawej i lewej stronie wektorowego równania ruchu, można otrzymać skalarne równania ruchu dla składowych prędkości w postaci
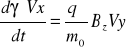
![]()
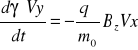
![]()
Uwzględniając, że
![]()
Przedstawione równania można przepisać jako
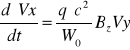
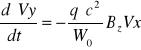
![]()
Powyższe równania mogą być sprowadzone do postaci
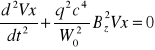
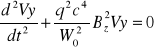
![]()
Przyjmując warunki początkowe dla czasu t=0 równe
![]()
![]()
![]()
Można pokazać, że rozwiązaniem przedstawionego układu równań są funkcje
![]()
![]()
![]()
Całkując równania prędkości cząstki względem czasu otrzymuje się równania jej trajektorii w postaci parametrycznej
![]()
![]()
![]()
W równaniach tych
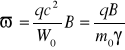
Częstotliwość W nazywana jest częstotliwością Larmora, częstotliwością cyklotronową lub żyroskopową. Jeśli Vxo=Vyo=Vo to trajektorię ruchu cząstki we współrzędnych x,y opisuje równanie okręgowe w postaci
![]()
Gdzie R jest promieniem tego okręgu równym
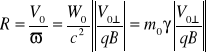
Akcelatory cząstek
Akceleratory czastek naładowanych sa stosowane w fizyce jadrowej do nadawania tym czastkom wysokich energii kinetycznych, rzedu milionów lub miliardów elektronowoltów. Tak duze energie sa niezbedne do wywołania szeregu reakcji jadrowych. Przykładem takiego akceleratora jest cyklotron,
zbudowany po raz pierwszy przez E. Lawrence'a w 1930 r (rys. 4.8).
Zasadnicza czesc cyklotronu stanowia dwa duanty o kształcie połówek niskiej, cienkosciennej puszki, umieszczone miedzy biegunami silnego elektromagnesu, który wytwarza pole magnetyczne o indukcji B. Do duantów przyłozone jest zmienne napiecie, wytwarzajace w szczelinie miedzy nimi zmienne pole elektryczne. Dodatni jon, znajdujacy sie poczatkowo w punkcie C jest przyspieszany przez pole elektryczne a nastepnie zakresla wewnątrz duantu półokrag o promieniu r danym wzorem (4.13).
W wyniku powtarzania tego procesu jon uzyskuje znaczna energie kinetyczna (w przypadku protonów — rzedu MeV). Warunkiem przyspieszania jonów jest równość okresu T0 zmian pola elektrycznego i okresu T obiegu jonu, określonego wzorem
Wartosc maksymalnej energii czastek, uzyskiwanej w cyklotronie, ogranicza głównie efekt wzrostu masy czastek z ich predkoscia, co narusza warunek synchronizmu obiegu, T0=T. Akceleratory w których
wyeliminowano ten efekt przez odpowiednia zmiane okresu napiecia zasilającego i indukcji pola magnetycznego podczas przyspieszania czastek nosza nazwe synchrofazotronów.
21. Magnetyczne właściwości materii. Opis mikroskopowy i właściwości makroskopowe.
Ze wzrostem wartości indukcji pola zewnętrznego, Bo wzrasta również, chociaż mniej intensywnie wartość indukcji B wewnątrz rdzenia ferromagnetycznego osiągającego wartość maksymalną odpowiadającą stanowi nasycenia. Krzywa ta nosi nazwę krzywej magnesowania pierwotnego. Przy stopniowym zmniejszaniu zewnętrznego pola magnetycznego (Bo), wartość indukcji B zamienia się, przy czym jej wartość Bs, któremu odpowiada zanik pola zewnętrznego nosi nazwę pozostałości magnetycznej zmieniając kierunek indukcji pola zewnętrznego na przeciwny, przy czym wartość indukcji w tym punkcie nosi nazwę pola koercji (niszczy pozostałość magnetyczną). Dalsze zwiększanie bezwzględnej wartości indukcji pola zewnętrznego powoduje wzrost ujemnej wartości indukcji magnetycznej wewnątrz rdzenia. W tym punkcie ponownie uzyskujemy stan nasycenia magnetycznego lecz przeciwnego znaku. Zmniejszając następnie wartość bezwzględną ujemnej indukcji pola zewnętrznego i wreszcie zmieniając jej kierunek na przeciwny (dodatni) otrzymujemy krzywą magnesowania rdzenia, której odpowiada pozostałość magnetyczna -Bs i koercja, oraz stan nasycenia. Okresowym zmianom wartości i kierunku indukcji Bo zewnętrznego pola magnetycznego odpowiada zamknięta krzywa zwana pętlą histerezy magnetycznej. Kształt pętli histerezy zależy od rodzaju materiału magnetycznego a pole jej powierzchni jest proporcjonalne do pracy zużytej na magnesowanie. Stal miękka wykazuje niewielką wartość koercji (wąska pętla) w skutek czego łatwo ją rozmagnesować. Stal krzemowa ma bardzo małą wartość pozostałości magnetycznej dlatego jest stosowana do wytwarzania rdzeni elektromagnesów, natomiast stal twarda oraz pewne stopy żelaza kobaltu, niklu, aluminium i miedzi, którym odpowiada duża wartość pozostałości magnetycznej i koercji (szeroka pętla histerezy) nadają się do wykonywania magnesów trwałych.
22. Fale elektromagnetyczne - opis. Charakterystyka widma promieniowania elektromagnetycznego.
Fale elektromagnetyczne - zaburzenia pola elektromagnetycznego rozchodzące się w przestrzeni ze skończoną prędkością. Fale elektromagnetyczne są falami poprzecznymi, tzn. w każdym punkcie pola wektor natężenia pola elektrycznego E i wektor indukcji magnetycznej B są prostopadłe do kierunku rozchodzenia się fal elektromagnetycznych i do siebie, a ich prędkość rozchodzenia się w próżni c m/s. Własności, warunki powstawania i rozprzestrzeniania się fal elektromagnetycznych opisują w zupełności równania falowe wynikające z równań Maxwella. Istotny wpływ na takie własności fal elektromagnetycznych, jak prędkość rozchodzenia się, polaryzacja, natężenie, ma ośrodek, w którym się fale elektromagnetyczne rozchodzą. W realnych ośrodkach występuje dyspersja fal elektromagnetycznych, tzn. zależność prędkości ich rozchodzenia się od częstości fali. Charakterystyczne dla fal elektromagnetycznych są zjawiska interferencji, dyfrakcji, załamania, oraz całkowitego wewnętrznego odbicia. Charakterystyka przestrzenno-czasowa fal elektromagnetycznych jest określana zarówno przez własności ośrodka, w którym się one rozchodzą, jak przez własności źródła promieniowania. Najprostszy przypadek wzbudzenia oraz rozprzestrzeniania się fal elektromagnetycznych stanowi wzbudzenie w jednorodnym ośrodku izotropowym za pomocą drgającego dipola Hertza. Stanowi go odcinek przewodu o długości l ( - długość wytwarzanej fali elektromagnetycznej), elektrycznie obojętny jako całość, opisany przez elektryczny moment dipolowy. W odległości od dipola dużo większej od tworzy się strefa falowa, gdzie rozchodzą się fale elektromagnetyczne poprzeczne, spolaryzowane liniowo.
Widmo fal elektromagnetycznych
Wszystkie fale można uszeregować wg częstotliwości. Taką klasyfikację fal nazywamy widmem fal elektromagnetycznych.
Widmo fal elektromagnetycznych nie ma granicy ani górnej ani dolnej.
Fale elektromagnetyczne poruszają się z prędkością światła i zależnie od długości fali przejawiają się jako (od fal najdłuższych do najkrótszych): fale radiowe, mikrofale, podczerwień, światło widzialne, ultrafiolet, promieniowanie X, promieniowanie gamma.
FALE RADIOWE
Fale elektromagnetyczne o częstotliwości 3 kHz - 3 THz (3*103 - 3*1012 Hz) (długości większej od 0,1 mm). Ze względu na długość fali (częstotliwość) rozróżnia się poszczególne typy fal radiowych. Istnieją dwa podziały: tradycyjny i dekadowy. Fale radiowe powstają przez wypromieniowanie energii z anteny nadawczej (układu nadawczego). Ze względu na środowisko propagacji wyróżnia się falę przyziemną (powierzchniową i nadziemną), falę troposferyczną, falę jonosferyczną i w przestrzeni kosmicznej. W zależności od długości fali radiowej jej propagacja jest poddana wpływowi różnorodnych zjawisk, np. dyfrakcji, refrakcji, odbicia od jonosfery itp. Źródłami naturalnymi są wyładowania atmosferyczne, gwiazdy, a sztucznymi nadajniki, silniki komutatorowe, komputery.
PROMIENIOWANIE PODCZERWONE
Promieniowanie podczerwone- niewidzialne promieniowanie elektromagnetyczne, formalnie zaliczane do fal świetlnych, o długości fali od 760 nm do 2000 µm. (Podczerwień (IR) to promieniowanie elektromagnetyczne mieszczące się w zakresie długości fal pomiędzy światłem widzialnym i mikrofalami. Podczerwień często dzieli się na bliską (NIR, 0,7-5µm), średnią (MIR 5-30µm) oraz daleką (FIR 30 - 1000 µm), ale są to tylko umowne granice). Emitowane jest przez rozgrzane ciała. W technice wytwarzane są przede wszystkim za pomocą specjalnych lamp żarowych, zw. promiennikami podczerwieni. Fale podczerwone, mające najniższą częstotliwość spośród wszystkich fal widzialnych, pobudzają do drgań nie tylko elektrony, ale i całe atomy oraz cząsteczki szkła. Dlatego też fale nazywa się często promieniowaniem cieplnym lub termicznym (obiekty w temperaturze pokojowej samoistnie emitują promieniowanie o takiej długości).
PROMIENIOWANIE GAMMA
Promieniowanie gamma strumień kwantów gamma (wysokoenergetyczna forma promieniowania elektromagnetycznego o długości fali poniżej 10 pm. Fale elektromagnetyczne większej długości fali to promieniowania X. Zgodnie z teorią fotonową można obliczyć, że foton promieniowania gamma ma energię większą niż 100 keV. Promieniowanie gamma jest zaliczane do promieniowania jonizującego razem z promieniowaniem alfa oraz promieniowaniem beta. Nazwa promieniowania gamma pochodzi od greckiej litery γ. Rozróżnienie promieniowania gamma oraz promieniowania X opiera się na ich źródłach a nie na długości fali). W otaczającym nas środowisku istnieje naturalne tło promieniowania gamma, którego źródłem są pierwiastki gamma promieniotwórcze zawarte w skorupie ziemskiej oraz promieniowanie kosmiczne. Mają najmniejszą długość fali i największą częstotliwość, mogą przenikać przez trzymetrową warstwę betonu. Niszczą wszystkie żywe komórki, także nowotwory (radioterapia). Promienie gamma mogą służyć do sterylizacji wyposażenia medycznego, jak również produktów spożywczych. Widmo promieniowania gamma pierwiastków promieniotwórczych ma charakter dyskretny, tj. obserwuje się oddzielne linie widmowe, energia odpowiadająca tym liniom pozwala indentyfikować promieniującą substancję.
![]()
PROMIENIOWANIE ULTRAFIOLETOWE
Promieniowanie ultrafioletowe promieniowanie elektromagnetyczne (świetlne) o częstotliwościach pomiędzy zakresem światła widzialnego (światło, fale elektromagnetyczne) a promieniowaniem rentgenowskim: odpowiada długości fali od 390 do ok. 10 nm (granica pomiędzy promieniowaniem ultrafioletowym a rentgenowskim jest umowna), dzieli się na ultrafiolet tzw. bliski (390-190 nm) i daleki (190-10 nm). Ultrafioletowe promieniowanie, choć niewidzialne, ma silne działanie fotochemiczne - przy długości fali poniżej 300 nm wywołuje już jonizację i jest zabójcze dla organizmów żywych. Znaczne ilości promieniowania ultrafioletowego emituje Słońce - Ziemię chroni przed nim warstwa ozonowa, pochłaniająca promieniowanie ultrafioletowe o długości fali poniżej 285 nm, a także powietrze, które pochłania całkowicie promieniowanie ultrafioletowe w zakresie ultrafioletu dalekiego.
PROMIENIOWANIE.X
Promieniowanie rentgenowskie jest to rodzaj promieniowania elektromagnetycznego (fale elektromagnetyczne) o długości fali zawartej w przedziale od 0,1 pm do ok. 50 nm, tj. pomiędzy promieniowaniem gamma i ultrafioletowym, przy czym zakres promieniowania rentgenowskiego pokrywa się częściowo z niskoenergetycznym (tzw. miękkim) promieniowaniem gamma - rozróżnienie wynika z mechanizmu wytwarzania promieniowania: promieniowanie rentgenowskie powstaje przy przejściach elektronów na wewnętrzne powłoki elektronowe atomu, natomiast promieniowanie gamma w przemianach energetycznych zachodzących w jądrze atomowym. Promieniowanie rentgenowskie może mieć zarówno widmo liniowe (promieniowanie charakterystyczne, Moseleya prawo, przy czym energia niesiona przez kwant charakterystycznego promieniowania X wyraża się wzorem hν=Ei-Ef, gdzie: h - stała Plancka, Ei, Ef, - odpowiednio energia stanu początkowego i końcowego elektronu w atomie), jak i widmo ciągłe (powstające jako promieniowanie hamowania w procesie oddziaływania cząstki naładowanej z materią, lampa rentgenowska).
Promieniowanie rentgenowskie wykorzystuje się w badaniach strukturalnych (rentgenowska analiza strukturalna, Braggów-Wulfa warunek, lauegram) oraz do badania pierwiastkowego składu chemicznego (rentgenowska analiza widmowa). Ponadto promieniowanie rentgenowskie szeroko stosuje się w diagnostyce medycznej (zdjęcia rentgenowskie).
MIKROFALE
Mikrofale, fale elektromagnetyczne znajdujące się w widmie pomiędzy falami ultrakrótkimi a podczerwienią (długość fali λ od 30 cm do 1 mm), bądź pomiędzy podczerwienią i falami radiowymi (co oznacza zakres 1mm-30cm (częstotliwość 1-300 GHz)). Mikrofale odkrył James Clerk Maxwell w 1864 roku. Stosowane w radiolokacji, telekomunikacji satelitarnej i w urządzeniach grzewczych (np. kuchenki mikrofalowe, która używa magnetronu do wytwarzania fal o częstotliwości ok 2,4 GHz, co pozwala na gotowanie jedzenia; taki rodzaj promieniowania działa na cząsteczki wody, które zaczynają drgać wytwarzając przez to ciepło). Do generacji mikrofal stosuje się specjalne lampy elektronowe (np. magnetron), masery lub generatory półprzewodnikowe (na bazie arsenku galu). W przesyłaniu mikrofal stosuje się falowody (popularnym sprzętem w gospodarstwie domowym jest kuchenka mikrofalowa będąca podstawowym elementem każdej kuchenki jest urządzenie wytwarzające fale elektromagnetyczne o dużej częstotliwości- mikrofale)
23.Oddziaływanie światła z materią.
Oddziaływanie światła z materią opisują zjawiska:
odbicia,
załamania
rozproszenia światła.
Odbicie światła
Prawo odbicia światła- Kąt odbicia β jest równy kątowi padania α. Promień padający, promień odbity i prostopadła padania (prostopadła do płaszczyzny odbijającej wystawiona w punkcie padania) leżą w jednym punkcie.
α=β
Całkowite wewnętrzne odbicie
Jeżeli światło przechodzi z ośrodka o większym współczynniku załamania do ośrodka o mniejszym współczynniku załamania (np. z wody do powietrza), opromień świetlny załamuje się tak, że kąt załamania jest większy niż kąt padania, przy czym istnieje taki kąt padania, zwany kątem granicznym, dla którego kąt załamania β=90˚. W przypadku gdy kąt padania jest większy niż kąt graniczny następuje zjawisko całkowitego wewnętrznego odbicia- promień świetlny całkowicie odbija się od granicy obu ośrodków.
Załamanie światła
Prawo załamania światła-Dla danych dwóch ośrodków stosunek sinusa kąta padania do sinusa kąta załamania jest równy stosunkowi prędkości światła w ośrodku pierwszym do prędkości światła w ośrodku drugim i nosi nazwę współczynnika załamania światła ośrodka drugiego względem pierwszego. Promień padający, promień załamany i prosta prostopadła do płaszczyzny ograniczającej oba ośrodki leżą w jednej płaszczyźnie.
sin α/sin β = v1/v2 = n21
α- kąt padania
β- kąt załamania
v1,v2- prędkość światła odpowiednio w ośrodku pierwszym i w drugim
n21- współczynnika załamania światła ośrodka drugiego względem pierwszego.
Rozproszenie światła
Rozproszeniem światła nazywamy zjawisko zmiany przestrzennego rozkładu wiązki światła na skutek oddziaływania z ośrodkiem rozpraszającym i objawiające się jako „niewłasne ” świecenie tego ośrodka. Świecenie to powstaje w skutek drgań elektronów w atomach ośrodka rozpraszającego wymuszonych przez światło padające. Rozproszenie światła zachodzi w ośrodku optycznie niejednorodnym, którego współczynnik załamania zmienia się w sposób nieregularny od punktu do punktu wskutek fluktuacji gęstości ośrodka lub obecności w ośrodku niewielkich cząstek innych substancji. W pierwszym przypadku rozproszenie światła nazywamy rozproszeniem cząsteczkowym (molekularnym) lub opalescencją, w drugim- rozproszeniem światła w ośrodkach mętnych.
Rozproszeniem liniowym światła nazywamy zjawisko zmiany przestrzennego rozkładu wiązki światła bez zmiany długości fali na skutek oddziaływania z powierzchnią lub ośrodkiem rozpraszającym.
24.Falowa natura światła. Interferencja, dyfrakcja światła i polaryzacja światła.
Falowa teoria światła tłumaczy bardzo dobrze:
zjawiska interferencji,
dyfrakcji
polaryzacji światła.
Interferencja światła
Zjawiska interferencji występują w przypadku fal na powierzchni wody, fal sprężystych, fal głosowych (podłużnych) w powietrzu, fal materii, itp.
Interferencja jest wynikiem nakładania się na siebie fal. Dla fal z którymi na ogół mamy do czynienia (a więc np. fal akustycznych, fal na powierzchni wody), a zwłaszcza dla fal świetlnych, obowiązuje zasada superpozycji (nakładania się) fal. Według tej zasady, jeżeli przez jakiś obszar w przestrzeni przechodzą dwie lub więcej fal, to każda z nich rozchodzi się tak, jak gdyby inne nie istniały. Wypadkowe działanie fal uzyskujemy poprzez geometryczne zsumowanie działań fal składowych.
W wyniku interferencji otrzymuje się obraz interferencyjny w postaci jasnych i ciemnych prążków (miejsc wzajemnego wzmacniania się i wygaszania światła docierającego z różnych źródeł).
Maksymalne wzmocnienie dwóch fal spójnych jest obserwowane w punktach, w których różnica dróg (różnica odległości punktu od obu źródeł nakładających się fal) Δr równa jest całkowitej wielokrotności długości fali:
Δr = nλ
Maksymalne wygaszenie dwóch fal spójnych jest obserwowane w punktach, w których różnica dróg Δr równa jest nieparzystej wielokrotności połówki długości fali:
Δr = (2n + 1)λ/2
Dyfrakcja światła
Dyfrakcja (ugięcie) światła polega na odchyleniu kierunku rozchodzenia się światła od kierunku pierwotnego, jeśli przechodzi ona przez niewielkie otwory lub szczeliny oraz kiedy natrafia na przeszkody. Efektem ugięcia światła jest obraz przedstawiający układ jasnych i ciemnych prążków. Szczególnie wyraźnie zjawisko dyfrakcji można zaobserwować przy przejściu światła przez siatkę dyfrakcyjną.
Zjawiska ugięcia się światła dzielimy według sposobu ich obserwacji na ugięcia Fresnela i ugięcie Fraunhofera. Przy fresnelowskim sposobie obserwacji na otwór czy przesłonę uginającą rzucamy z punktu świetlnego rozbieżną wiązkę światła i obserwujemy interferencje wiązek zbieżnych. Inaczej mówiąc, źródło światła i punkt obserwacyjny znajdują się w skończonej odległości od ekranu, tj. w strefie bliskiej. Przy metodzie Fraunhofera rzucamy na uginający ekran równoległą wiązkę promieni i obserwujemy również interferencje wiązek równoległych. Przy tej metodzie obserwacji źródło światła i punkt obserwacyjny znajdują się w nieskończonej odległości od ekranu czyli w strefie dalekiej.
Jakościowo zrozumieć zjawisko dyfrakcji pozwala zasada Huygensa. Według niej każdy punkt do którego dociera czoło fali rozchodzącej się w jakimś ośrodku staje się źródłem elementarnej fali cząstkowej (kulistej w przestrzeni, kolistej na powierzchni). Powierzchnia styczna do wszystkich fal cząstkowych stanowi powierzchnie fali wypadkowej.
Polaryzacja światła.
Zjawisko polaryzacji dotyczy wyłącznie fal poprzecznych i polega na uporządkowaniu drgań ośrodka. Światło jest falą elektromagnetyczną, więc ma charakter fali poprzecznej. Kierunek polaryzacji fali elektromagnetycznej jest taki, jak kierunek pola elektrycznego o wektorze E (przez płaszczyznę polaryzacji należy rozumieć płaszczyznę zawierającą wektor E oraz kierunek rozchodzenia fali). Światło, w którym drgania pola elektrycznego odbywają się w różnych kierunkach, nazywamy niespolaryzowanym. Jego polaryzacja polega na uporządkowaniu drgań wektorów natężenia pola elektrycznego E. Światło może być spolaryzowane:
liniowo - drgania pola elektrycznego odbywają się tylko w jednym kierunku,
kołowo - kierunek drgań obraca się cyklicznie (koniec wektora pola elektrycznego fali biegnącej zakreśla linie śrubową o przekroju kołowym).
Polaryzacja światła zachodzi podczas :
załamania,
rozproszenia,
odbicia.
25. Dualizm korpuskularno-falowy. Koncepcje i zjawiska.
Dualizm korpuskularno-falowy
Właściwość materii (w szczególności cząstek) polegająca na tym, że w pewnych sytuacjach ujawnia się jej natura falowa, w innych zaś- korpuskularna. Elektrony, które uważane są zwykle za klasyczne cząstki ulegają dyfrakcji na sieciach krystalicznych, a więc uczestniczą w zjawisku typowo falowym. To samo tyczy neutronu. Światło, którego natura falowa nie ulega wątpliwości (świadczą o tym zjawiska: dyfrakcji, interferencji i polaryzacji światła, które są zjawiskami typowymi dla fal), w takich zjawiskach jak fotoefekt lub zjawisko Comptona, zachowuje się jak zbiór cząstek. Uznanie dwoistej natury materii jest podstawą fizyki współczesnej, a w szczególności mechaniki kwantowej oraz kwantowej teorii pola.
Koncepcje i zjawiska
Dylemat: cząstka czy fala
Od czasów filozofów starożytności aż do Izaaka Newtona uczeni uważali, że światło są to szybko poruszające się korpuskuły. W 1801 r. interferencyjne doświadczenia Thomasa Younga ugruntowały falową teorię światła na mocnych podstawach doświadczalnych i wydawało się w tym czasie, że fizycy mogliby odrzucić ideę korpuskularnej struktury światła. Jednakże teorie korpuskularne zaczęły odpowiadać na coraz więcej pytań dotyczących fizycznych własności ciał stałych, cieczy i gazów. Pod koniec XIX wieku doświadczenia J.J. Thomsona i H. A. Lorentza doprowadziły do koncepcji korpuskuły elektryczności- elektronu. Ostatecznie koło się zamknęło ok. 1900 roku, kiedy sformułowano prawo promieniowania ciała doskonale czarnego na podstawie postulatu Maxa Plancka głoszącego, że źródło światła nie emituje promieniowania w sposób ciągły, lecz w skończonych porcjach, zwanych kwantami. Około 1923r. dylemat cząstka czy fala, znów wypłynął wyraźnie, kiedy A. Compton odkrył, że kwanty promieniowania X mają zarówno pęd, jak i energię. Wydawało się więc, że światło ma dwa odrębne zespoły własności, które są ze sobą sprzeczne.
W 1924r. Louis de Broglie przedstawił swoją pracę doktorską pt. „Badania nad teorią kwantów”, w której zasugerował, że skoro światło ma wiele cech korpuskularnych, więc cząstki, a w szczególności elektrony, ze względu na symetrię w przyrodzie powinny wykazywać cechy falowe. W 1927 r. jego idee zostały sprawdzone przez G. P. Thomsona oraz niezależnie od niego przez C. J. Davissona i L. G. Germera, którzy pokazali, że elektrony, podobnie jak światło, mogą ulegać dyfrakcji.
Fale de Broglie`a.
Planck powiązał energię świetlnych korpuskuł (fotonów) z częstością światła relacją:
E=hν, (10.1)
gdzie ν jest częstością fotonu, a energia E ma postać taką jak w szczególnej teorii względności, czyli E=E0+K, z tym że w wypadku fotonu E0=m0c2=0 i całkowita energia E=K jest wyłącznie energią kinetyczną. Jednakże w czystej teorii korpuskularnej nie ma miejsca na pojęcie częstości. De Broglie rozumował, że muszą istnieć pewnego rodzaju fale związane z fotonami, aby można było wyjaśnić tak czysto falowe zjawisko jak interferencja. Compton pokazał, że fale świetlne mają pęd, zwykle przypisywany jedynie cząstkom. Wyrażenie na energię fotonu może być również przedstawione w postaci:
E=mc2=pc, (10.2)
Gdzie p jest pędem przypisanym fotonowi. Kombinacja równań (10.1) i (10.2) prowadzi do wyrażenia
p=![]()
,(10.3)
a więc do związku falowych własności fotonów: długości fali λ i częstości ν z własnością korpuskularną - pędem p.
Na podstawie tego związku de Broglie wysunął zaskakującą ideę: jeżeli światło może mieć naturę korpuskularną, to cząstki takie jak elektrony mogą mieć cechy falowe. Pęd elektronu można zatem zapisać przez analogię w postaci:
p=mν=![]()
,(10.4)
gdzie m jest masą relatywistyczną. Wyrażenie to przypisało cząstce, jaką jest elektron, cechę falową, tj. długość fali λ. Z równania (10.4) wynika, że długość fali elektronu
![]()
,(10.5)
Może być wyrażona za pomocą pędu jako:
![]()
,(10.6)
Gdzie p=(1/c)![]()
na podstawie równania (6.25). Wobec tego
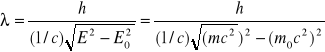
,
Co można przekształcić w
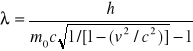
I uprościć do
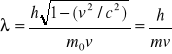
,
26. Budowa atomu. Model Bohra. Postulaty.
Atom- najmniejsza cząstka pierwiastka chemicznego, która jeszcze posiada jego własności chemiczne i fizyczne. W przyrodzie istnieje tyle atomów ile występuje w niej pierwiastków istnieją w odmianach różniących się masą atomową tzw. izotopy. Atom jest układem cząstek elementarnych składającym się z dodatnio naładowanego jądra atomowego i otaczającej je chmury elektronowej. Praktycznie cała masa atomu skupiona jest w jego jądrze, którego rozmiar jest ok. 10000 razy mniejszy od rozmiaru atomu. Jądro składa się z protonów i neutronów zwanych nukleonami. Ładunek jądra równy jest liczbie protonów pomnożonej przez dodatni ładunek elementarny. Liczba elektronów w atomie równa jest liczbie protonów i jest to tzw. atomowa liczba Z. Liczbę nukleonów w jądrze nazywamy liczbą masową A. Obie te liczby umieszcza się w symbolu atomu pierwiastka, np.![]()
Na oznacza, że atom sodu zawiera 23 nukleony, w tym 11 elektronów. Oznacza to także, że powłoka elektronowa tego atomu zawiera 11 elektronów. Atomy mają rozmiary rzędu 10-10m, a ich masy zawierają się w granicach między 10-27 i 10-25 kg. Oddziaływanie jądra atomowego z chmurą elektronową ma charakter elektrostatyczny, podczas gdy protony i neutrony w jądrze związane są siłami jądrowymi. Stany energetyczne atomu są dyskretne, co oznacza, że pochłania on i emituje energię ściśle określonymi porcjami. Przejawem tego są dyskretne (liniowe) widma emisyjne i absorpcyjne atomów pozwalające na ich identyfikację (podobnie jak odcisk palca u człowieka).Obecne poglądy na budowę atomu bazują na bardzo poglądowym modelu zaproponowanym w 1913 r. przez N. Bohra (atom Bohra), ale dokładny opis własności atomów powstał dopiero na gruncie mechaniki kwantowej. W opisie tym elektron krążący po ściśle określonej orbicie został zastąpiony przez rodzaj fali stojącej, nazywanej często chmurą elektronową lub obszarem orbitalnym. Nie jest to zwykła chmura; jej gęstość określa prawdopodobieństwo znalezienia elektronu w określonym punkcie przestrzeni. Stan każdego elektronu w atomie charakteryzują 4 liczby kwantowe związane z takimi wielkościami fizycznymi, jak: energia, orbitalny moment pędu, rzut momentu pędu na wyróżniony kierunek w przestrzeni, rzut własnego momentu pędu elektronu (spin) na wyróżniony kierunek. Liczby kwantowe opisują tzw. stan kwantowy elektronu. W atomie w określonym stanie kwantowym może znajdować się tylko jeden elektron (zakaz Pauliego).
Atom Bohra
Został on sformułowany po odkryciu przez E. Rutherforda istnienia dodatnio naładowanego jądra atomowego i nazywany jest czasem modelem planetarnym. W modelu tym elektrony krążą po kołowych orbitach wokół jądra atomowego, podobnie jak planety krążą wokół Słońca. Oddziaływanie jądra atomowego z elektronem jest oddziaływaniem elektrostatycznym. Istotę modelu stanowią jednak trzy tzw. postulaty Bohra:
elektron może poruszać się jedynie po takich orbitach, na których jego moment pędu jest wielokrotnością h/2π (h- stała Plancka). Orbita taka jest stacjonarna i poruszający się po niej elektron nie emituje energii;
emisji lub pochłonięciu elektronu przez atom towarzyszy przejście elektronu z jednej orbity stacjonarnej na inną;
częstotliwość promieniowania emitowanego przez atom równa jest ν= (E2-E1)/h, gdzie E1i E2 - energie elektronu odpowiednio na bliższej i dalszej orbicie.
Sukcesem tego modelu atomu było wyjaśnienie widma promieniowania atomu wodoru i pojedynczo zjonizowanego helu.
Masa atomu[z notatek dr Ledziona]
Z obserwacji doświadczeń chemicznych i z prawa Daltona stałych stosunków wielokrotnych oraz z hipotezy Avogadra otrzymano, że masy atomowe różnych pierwiastków są w przybliżeniu całkowitymi wielokrotnościami masy atomowej atomu wodoru;
Początkowo więc jedna jednostka masy atomowej 1u (1 amu) była równa masie atomu wodoru;
Od 1961 roku do definicji jednostki masy atomowej wykorzystywana jest masa atomu węgla 12C, która wynosi 12.0000u, zatem 1u nie jest równy masie atomu wodoru, która wynosi 1.007825u.
1u=![]()
Masę atomową można otrzymać posługując się względnymi masami atomowymi i wykorzystując pojęcie mola.
Def. Avogadra: 1 mol substancji jest to ilość gramów danej substancji równa się względnej masie atomowej tej substancji. W przypadku cząsteczki chemicznej równa jest jej względnej masie cząsteczkowej.
1mol izotopu węgla 12C odpowiada 12 gramom tej substancji
1mol zawiera taką samą liczbę NA atomów (cząsteczek)
Jądrowe modele atomu :
model atomu Thomsona
model atomu Rutherforda
model atomu Bohra
model atomu Sommerfelda
Model atomu Bohra. Postulaty Bobra:
Elektrony poruszają się wokół jądra jednostajnym ruchem kołowym w wyniku działania sił kulombowskich i zgodnie z zasadami dynamiki Newtona
Elektrony poruszają się po pewnych dozwolonych orbitach, dla któ®ych moment pędu można wyrazić zależnością:
L= mVr= n![]()
, n=1,2,3…
Elektron, który porusza się po dozwolonej orbicie nie promieniuje energii
Podczas przejścia elektronu z jednej orbity na inną jest emitowany lub pochłaniany kwant promieniowania elektromagnetycznego o częstotliwości:
![]()
Stany energetyczne w modelu Bohra dla atomu wodoru
E= -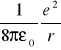
L= mVr= n![]()
, n=1,2,3…
V=![]()
Energia kinetyczna może być zapisana w postaci:
Ek=![]()
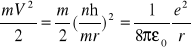
Z równania opisującego energię kinetyczną możemy otrzymać wyrażenie:
rn=![]()
Dla stanu podstawowego n=1 promień orbity wynosi:
r1=5.3·10-11m
Całkowita energia atomu może być zapisana w postaci:
E=-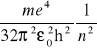
Zatem konsekwencją postulatów Bohra jest nie tylko kwantyzacja momentu pędu, energii kinetycznej czy promienia orbity dozwolonej ale również kwantyzacja całkowitej energii.
Energia wzbudzenia Ea, jest to energia jaką trzeba dostarczyć atomowi aby przenieść elektron ze stanu podstawowego do stanu wzbudzonego;
Energia jonizacji Ej jest to energia potrzebna do uwolnienia elektronu z atomu, kiedy elektron znajduje się w stanie podstawowym;
Energia wiązania Ew jest to energia dla danego stanu atomu, którą należy dostarczyć atomowi aby usunąć z niego elektron, gdy atom znajduje się w danym stanie wzbudzonym.
Model Bohra i zasada korespondencji.
V=ωr=2πνr 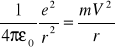
Skąd otrzymujemy wyrażenie:
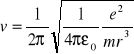
Wykorzystując wyrażenie na częstotliwość i promień orbity otrzymujemy:
rn=![]()
; 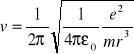
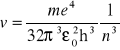
Z modelu Bohra wyrażenie na częstotliwość można zapisać:
![]()
; E=-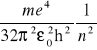
;
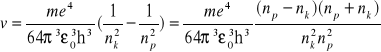
![]()
=Δn
![]()
=2np=2n
![]()
≈n4
27. Reakcje jądrowe. Rozszczepienie, synteza jądrowa.
Siły jądrowe są bardzo mocne - ich wartość jest ponad 1040 razy większa od wartości sił grawitacyjnych, jednak ich zasięg wynosi zaledwie ok. 10-15 m. Na dwa nukleony znajdujące się blisko siebie działa siła przyciągania jądrowego znacznie większa od siły odpychania Coulomba. Jednak jeżeli będziemy je od siebie odsuwać, siła przyciągająca będzie gwałtownie maleć i w pewnym momencie silniejsza stanie się siła odpychająca.
Nukleon oddziaływuje za pośrednictwem sił jądrowych tylko z sąsiadującym nukleonem, więc przy wzroście liczby nukleonów w jądrze siła oddziaływania jądrowego przypadająca na jeden nukleon rośnie tylko do momentu, kiedy nukleon nie może mieć już większej ilości "sąsiadów". Natomiast siła odpychania wzrasta prawie proporcjonalnie do ilości protonów w jądrze. Wszystkie jądra o liczbie atomowej Z > 82 (oraz niektóre o Z =< 82) nie są stabilne, więc ulegają samoczynnym rozpadom, zwanym rozpadami promieniotwórczymi (samorzutnymi).
Rozpady samorzutne polegają na emisji cząsteczek (czyli jąder 42He), cząsteczek (elektronów) lub promieni γ (fal elektromagnetycznych) i przemianie w inne jądro.
Rozpad
Przemianie tej przypisuje się ogólne równanie:
AZX
A-4Z-2Y + 42He
Ulega jej np. jądro radu-226 zamieniając się w jądro radonu-222:
22688Ra
22286Rn + 42He
Rozpad
Przemiana ta przebiega zgodnie z równaniem:
AZX
AZ+1Y + 0-1e
Ulega jej m.in. jądro aktynu-227 przekształcając się w jądro toru-227:
22789Ac
22790Th + 0-1e
Bardzo interesujące jest zagadnienie, skąd w jądrze biorą się elektrony. Nurtowało ono umysły naukowców początku ubiegłego stulecia. Poprawną odpowiedź udzielił dopiero Wolfgang Pauli w roku 1931. Stwierdził, że podczas przemiany jeden z neutronów w jądrze zamienia się w proton, elektron i neutrino. Neutrino nie posiada ładunku i, przypuszczalnie, masy. Elektron i neutrino zostają wypromieniowane, a proton zostaje w jądrze. Istnienie neutrina zostało udowodnione ok. 1954 roku.
Podobnie jak elektrony w atomie, w samym jądrze nukleony też znajdują się na pewnego rodzaju orbitach. Na wyższej orbicie może się znaleźć po wyemitowaniu przez jądro jakiejś cząsteczki. Gdy znajdzie się na wyższej orbicie, może przeskoczyć na niższą, wolną, emitując przy okazji fotony - promienowanie γ. Dlatego towarzyszy ono innym rodzajom promieniowania.
Reakcje jądrowe
Do reakcji jądrowej (sztucznej przemiany jądrowej) może dojść podczas zderzenia się jądra z cząstką elementarną lub innym jądrem. Tworzy się wtedy nowe jądro i wypromieniowywana jest nowa cząstka.
Gdy skieruje się strumień cząstek na przedmiot wykonany z uranu nastąpi przemiana:
42He + 23892U
24194Pu + 10n
dzięki tego typu przemianom otrzymano m.in. transuranowce, pierwiastki nie występujące w przyrodzie. Bombardując neutronami cząsteczkę rtęci można dokonać jej przemiany w złoto, czyli dokonać transmutacji metali, o czym przez wiele wieków marzyli alchemicy. Niestety, taka przemiana jest nieopłacalna więc nie wykorzystuje się jej do otrzymywania drogocennego metalu...
Rozszczepienia jądrowe
Rozszczepienie (podział) jądra ciężkiego może nastąpić samorzutnie lub po zderzeniu z cząstką. Przemianie tej towarzyszy wypromieniowanie cząstek elementarnych. Np. jądro uranu-235 po zderzeniu się z neutronem rozpada się według schematu:
10n + 23592U
14156Ba + 9236Kr + 3 10n
część jąder 235U rozpada się na inne sposoby. Charakterystyczne jest, że zawsze jedno jądro jest trochę większe od drugiego. Rozszczepieniu jądrowemu towarzyszy wydzielenie się dużej ilości energii. Z tego powodu rozszczepienie 235U wykorzystuje się w elektrowniach jądrowych i bombach atomowych.
Fuzje jądrowe
Fuzja jądrowa (synteza jądrowa, reakcja termojądrowa, termonuklearna) to przemiana polegająca na utworzeniu jednego jądra przy zderzeniu dwóch jąder lekkich. Np.
21H + 31H
42He + 10n
Podczas fuzji jądrowej uwalniana jest niewyobrażalna ilość energii, dlatego tę przemianę wykorzystuje się w tzw. bombach wodorowych, znacznie silniejszych od bomb atomowych.
Reakcjami jądrowymi rządzą następujące prawa:
Zachowanie ładunku elektrycznego. Całkowita liczba protonów przed reakcją jest równa całkowitej liczbie protonów po reakcji.
Zachowanie liczby nukleonów (protonów i neutronów). Całkowite liczby masowe przed i po reakcji są takie same.
Zachowanie masy-energii. Dla danego układu izolowanego podlegającego przemianie jądrowej stała jest suma energii (masa związana jest z energią przez równanie Einsteina E=mc2).
Zachowanie pędu.
Zachowanie momentu pędu.
28. Rozpady promieniotwórcze. Charakterystyka promieniowania alfa, beta i gamma.
Promieniotwórczość - zdolność wysyłania przez różne izotopy promieniowana korpuskularnego lub gamma na skutek rozpadu jąder atomowych.
Rozpad promieniotwórczy - samorzutna przemiana jąder w inne, której towarzyszy emisja promieniowania.
Rozpadom promieniotwórczym podlegają jądra nietrwałe. Emitują one spontanicznie cząstki β lub α oraz promieniowanie elektromagnetyczne, przez co pozbywają się energii i zamieniają się w jądra bardziej stabilne.
Prawo rozpadu promieniotwórczeg- Prawo to określa zmianę w czasie liczby rozpadających się jąder. Dla każdego jądra prawdopodobieństwo rozpadu na jednostkę czasu jest stałe i nie zależy od warunków fizycznych i nie zależy od chemicznych powiązań danego pierwiastka.
Niech N - liczba atomów pierwiastka, dN - liczba atomów, które mogą się rozpaść w krótkim czasie dt. Mamy:
![]()
Znak „-” oznacza ubytek. Rozwiązując to równanie i przyjmując warunki początkowe, że w chwili t równej zero było N0 atomów otrzymamy:
![]()
Współczynnik proporcjonalności λ to tzw. stała rozpadu. Jej jednostką jest [s-1]. Określa ona stosunek liczby atomów rozpadających się w ciągu jednej sekundy do wszystkich atomów próbki danego pierwiastka w danej chwili czasu.
Cechą charakterystyczną każdego pierwiastka promieniotwórczego jest okres połowicznego zaniku, czyli czas, w którym liczba atomów maleje do połowy:
![]()
Innym pojęciem, które charakteryzuje rozpad promieniotwórczy jest aktywność. To liczba rozpadów zachodzących w jednostce czasu:
![]()
Znając dN / dt z prawa rozpadu mamy:
![]()
przy czym λN jest to aktywność A0 nuklidu w chwili początkowej. Jednostką aktywności jest bekerel.:
1 Bq = s-1.
Wszystkie rozpady promieniotwórcze podlegają trzem zasadom:
zasadzie zachowania liczby nukleonów,
zasadzie zachowania ładunku,
zasadzie zachowania pędu i energii.
Pierwiastki promieniotwórcze tworzą rodziny (szeregi) promieniotwórcze. Każdy człon szeregu jest potomkiem pierwiastka macierzystego rodziny, powstałym w wyniku rozpadu promieniotwórczego alfa lub beta. Kwanty gamma są emitowane wtedy, gdy na skutek rozpadu powstaje jądro wzbudzone. Znane są 4 rodziny promieniotwórcze:
torowa - liczba masowa wszystkich pierwiastków rodziny zmienia się według wzoru A = 4n; początek od toru 90,
neptunowa - pluton 94; A = 4n + 1; otrzymywana sztucznie, bo plutonu już nie ma w złożach naturalnych,
uranowa - uran 92; A = 4n + 2,
aktynowa - uran 92; A = 4n + 3.
Wszystkie rodziny naturalne kończą się na jakimś izotopie ołowiu, a rodzina neptunowi na trwałym bizmucie.
Rozpad alfa. Jądro atomu macierzystego emituje jądro helu, czyli cząstkę α. Powstały atom ma ładunek jądra mniejszy o 2 ładunki elementarne i masę mniejszą o 4 jednostki mas atomowych:
![]()
Jest to prawo przesunięć Soddy'ego i Fajansa, a E to energia wyzwolona podczas przemiany, która ujawnia się jako energia kinetyczna cząstki wyrzuconej i energia kinetyczna powstałego jądra. Skoro cząstki α są emitowane z jąder, to zanim to się stanie, muszą przebywać w ich wnętrzu. Pomiędzy cząstką α i reszta jądra musi działać siła coulombowska odpychająca, a dodatkowo we wnętrzu jądra działają siły jądrowe. W miarę przybliżania cząstki α do jądra rośnie jej odpychanie. Jednak dla pewnej odległości rzędu 10-14 - 10-15 m siły odpychające zmieniają się gwałtownie na przyciągające i cząstka wciągana jest do jądra. Tam stały potencjał tworzący barierę dla cząstki, z punktu widzenia fizyki klasycznej nie pozwoli jej opuścić jądra dopóki cząstka nie osiągnie wymaganej energii kinetycznej. Jednak okazuje się, że energie cząstek α są na ogół mniejsze niż bariera potencjału. Emisję cząstki α tłumaczy kwantowy efekt tunelowy. Cząstka α nie musi być odbita od bariery, ale może przez nią przeniknąć. Prawdopodobieństwo przeniknięcia cząstki α przez barierę opisane jest wzorem:
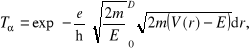
gdzie D to przenikalność bariery.
Promieniowanie α w porównaniu z innym promieniowaniem ma dużą masę, więc jego zasięg jest najmniejszy (w powietrzu jest to kilka cm). Ale ze względu na masę i fakt posiadania ładunku cząstki α bardzo szybko przekazują energię do ośrodka, w którym się prouszają. Rozpad α jest najbardziej prawdopodbnym rozpadem dla jąder ciężkich i nie występuje właściwie odrzut jądra.
Rozpad beta. W wyniku tej przemiany do jądra zostaje wchłonięty lub wyemitowany elektron. Istnieje jeszcze tzw. wychwyt K.
Rozpad β- - emitowane są negaton i antyneutrino: ![]()
Rozpad β+ - emitowane są pozyton i neutrino: ![]()
Izotopy podlegające rozpadowi β- to: jod 131, tryt, fosfor 31, a rozpadowi β+ fosfor 30, sód 22.
Widmo promieniowania β jest ciągłe, czyli nie jest monoenergetyczne. Wynika to z przyjętej przez Pauliego koncepcji neutrino i antyneutrino (1931r.). Energia rozpadu dzieli się w sposób przypadkowy na trzy części (energie: odrzutu jądra, elektronu / pozytonu i neutrino / antyneutrino) i dlatego wyemitowane cząstki β mają różne energie. Gdyby nie istniało neutrino, to podczas tych rozpadów następowałaby zmiana spinu jądra macierzystego, ponieważ spin elektronu jest połówkowy. Neutrino także posiada spin połówkowy, ale skierowany przeciwnie do spinu pozytonu. Spin wypadkowy wynosi 0, więc spin jądra ulegającego rozpadowi nie zmienia się. Promieniowanie β ze względu na niewielką masę cząstek jest bardzo przenikliwe, a jego zasięg w powietrzu wynosi kilkadziesiąt cm.
Wychwyt K. Jądro wciąga do wnętrza jeden z elektronów powłokowych (najczęściej z powłoki K). Następuje przy tym emisja neutrino, a elektron zobojętnia jeden ładunek dodatni jądra:
![]()
Podczas tego wychwytu nie występuje promieniowanie cząsteczkowe, więc całą energię rozpadu unosi ze sobą neutrino. Wolne miejsce po elektronie na powłoce jest szybko zapełniane przez elektrony z powłoki L, na powłokę L przeskakują wtedy elektrony z powłoki M itd. Następuje emisja kwantów promieniowania charakterystycznego.
Rozpad gamma. Rozpad ten towarzyszy rozpadom α i β, ponieważ po emisji tych cząstek jądro powstałe bardzo często jest w stanie wzbudzonym. Po pewnym czasie przechodzi ono do stanu podstawowego, emitując kwant γ o energii:
![]()
Liczby atomowa i masowa nie zmieniają się. Przy rozpadzie α fotony promieniowania γ mają niedużą energię, mniejszą niż 0,5 MeV, a powstałe podczas rozpadu β mają energie dużo większe (osiągają do 2,5 MeV). Powstałe promieniowanie elektromagnetyczne nie posiada ładunku elektrycznego i jest najbardziej przenikliwe. Nie ulega ono spowolnieniu tak jak cząstki α i β, tylko w czasie przechodzenia przez materię maleje jego natężenie.
29. Wytwarzanie, własności i detekcja promieniowania X.
Promienie rentgenowskie (promienie X) - Zostało odkryte 1895 przez W.C. Röntgena. Jest to promieniowanie elektromagnetyczne o fali długości od ok. 0,0001 nm do ok. 100 nm; powstaje w wyniku hamowania cząstek naładowanych przez materię (tzw. promieniowanie hamowania) lub w rezultacie przejścia elektronów w atomach (zjonizowanych w powłoce wewnętrznej, np. przez bombardowanie materii elektronami) z poziomów o wyższej energii na poziomy o energii niższej (tzw. promieniowanie charakterystyczne. Źródłem promieniowania rentgenowskiego są różnego rodzaju lampy rentgenowskie, pierwiastki promieniotwórcze, akceleratory cząstek, a także wiele ciał niebieskich.
Wytwarzanie promieniowania rentgenowskiego w lampie rentgenowskiej:
Podgrzana katoda jest źródłem elektronów, które następnie są przyspieszane napięciem przyspieszającym, osiągając duże energie. W bańce jest próżnia, by elektrony nie rozpraszały się na cząsteczkach powietrza. Rozpędzone elektrony padają na anodę i zostają w niej wyhamowane, a każdy ładunek, który ulega przyspieszeniu emituje fale elektromagnetyczne. Więc jeśli elektrony miały duże prędkości (co uzyskuje się przez przyłożenie różnicy potencjałów rzędu kilku tysięcy woltów), a proces hamowania był szybki, to uzyskuje się silne promieniowanie elektromagnetyczne.
Jest to najprostsza lampa rentgenowska i nie uwzględniono tu chłodzenia anody, co w warunkach doświadczalnych jest konieczne. Najczęściej chłodzi się przepływającą wodą, ale także robi się tzw. wirujące anody: anoda jest w kształcie tarczy, która wiruje po to, by elektrony uderzały za każdym razem w inne miejsce.
Zgodnie z prawami fizyki klasycznej w wyniku hamowania elektronów w materiale tarczy, aż do ich całkowitego zatrzymania, następuje emisja promieniowania elektromagnetycznego o widmie ciągłym. Jednak może się zdarzyć, że elektron uderzając w anodę nie tylko zostanie wyhamowany, ale może wybić elektron z atomu anody. Zostanie dziura, którą wypełni elektron spadający z wyższych powłok, z czym związane jest promieniowanie charakterystyczne dla danego pierwiastka. Dlatego ostatecznie wykres przedstawia widmo ciągłe promieniowania X z ostrymi pikami promieniowania charakterystycznego.
Właściwości i cechy:
Promieniowanie rentgenowskie dzieli się na: promieniowanie rentgenowskie miękkie, o większej długości fali, mniej przenikliwe, i promieniowanie rentgenowskie twarde, o mniejszej długości fali, bardziej przenikliwe.
Podczas przechodzenia przez materię promieniowanie rentgenowskie jest absorbowane i rozpraszane; ulega dyfrakcji, interferencji, polaryzacji, załamaniu i całkowitemu odbiciu; powoduje zaczernienie emulsji fotograficznej, wywołuje jonizację gazów, fluorescencję i fosforescencję niektórych substancji, reakcje fotochemiczne i zmiany w komórkach organizmów (mutacja); dla oka jest niewidzialne.
Pomieniowanie rentgenowskie jest wykorzystywane m.in.: do celów leczn. (rentgenodiagnostyka, rentgenoterapia), badania składu chem. substancji (rentgenospektralna analiza) oraz badania struktur kryształów (krystalografia rentgenowska, rentgenostrukturalna analiza).
Wykrywanie:
Wykrywa się je i bada m.in. za pomocą ekranu luminescencyjnego, błon fot., liczników: Geigera-Müllera, scyntylacyjnych, proporcjonalnych. Zasada pomiaru tych mierników bazuje głównie na zjawisku jonizacji i jego następstwach.
30. Oddziaływanie promieniowania jonizującego na organizmy żywe.
Oddziaływanie promieniowania jonizującego z żywą tkanką można podzielić na 4 stadia.
Stadium fizyczne - na skutek jonizacji lub wzbudzenia zmieniają się właściwości molekuł tkanki i zachodzą pierwotne procesy chemiczne w "gniazdach", gdzie cząstki promieniowania pozostawiły porcje energii.
Stadium fizyko-chemiczne - powstałe wcześniej produkty ulegają dalszym rekombinacjom i reakcjom, tworząc wolne rodniki lub rodniko-jony.
Stadium chemiczne - wolne rodniki powstałe w obszarach pochłonięcia energii dyfundują (m.in. odprowadzone zostają z krwią) i reagują z coraz dalszymi (od toru cząsteczki promieniowania jonizującego) obszarami tkanki. Największe uszkodzenia w tkankach wywołać może rodnik wodorotlenowy OH*. Jako silny utleniacz może on przekształcić normalne DNA w rodnik DNA - bardzo aktywną substancję zdolną do zainicjowania poważnych zmian funkcjonalnych właściwości komórek, łącznie z uniemożliwieniem ich funkcjonowania aż do śmierci komórki.
Stadium biologiczne - żywy organizm reaguje na zmianę właściwości składników komórki (tkanki): następują zaburzenia funkcjonalne (niekiedy bardzo opóźnione w czasie), które mogą ujawnić się w postaci zmian klinicznych. Należy pamiętać, że o ile czas trwania trzech pierwszych stadiów działania promieniowania jonizującego jest rzędu 10-8 sekundy, to czas trwania stadium biologicznego jest w ogromnym stopniu uzależniony od wszystkich czynników określających wrażliwość organizmu na promieniowanie jonizujące oraz od ilości zaabsorbowanej energii.
Zestaw szkodliwego oddziaływania promieniowania jądrowego na organizm ludzki leżą procesy jonizacji zachodzące w komórkach organizmu pod wpływem promieniowania.
Cząstki naładowane oddziaływując z tkankami organizmu, powodująjonizację bezpośrednio, natomiast cząstki nienaładowane (neutrony, kwanty gamma) w wyniku oddziaływania powodują powstanie cząstek naładowanych (p, e), które następnie wywołują jonizację. Neutrony szybkie powodują powstanie w substancji protonów, a neutrony termiczne wywołują w substancji reakcje jądrowe, w wyniku których powstają fotony, cząstki naładowane i jądra promieniotwórcze. Jonizacja może naruszać istotną strukturę komórki lub może oddziaływać pośrednio poprzez reakcje chemiczne, które zapoczątkowuje. W drugim przypadku podstawowe znaczenie ma zapoczątkowane przez jonizację zjawisko radiolizy wody (zawartość wody w organizmie człowieka wynosi około 70%) prowadzące do
pojawienia się wysoce aktywnych chemicznych rodników H i OH . Ich obecność może spowodować zaburzenia przemian metabolicznych organizmu (czynności enzymatycznych, syntezy białek itp.). Komórka reaguje na promieniowanie różnie w różnych okresach swego rozwoju, najłatwiej ulegając uszkodzeniu we wczesnych fazach."
Można wyróżnić trzy rodzaje efektów działania biologicznego promieniowania:
1. "Efekty somatyczne - polegają na uszkadzaniu radiacyjnym komórek podtrzymujących procesy życiowe; mogą one przejawiać się wprost w ciele napromieniowanego osobnika po kilku minutach lub tygodniach, a nawet później - po latach. Związane są one z pewną progową liczbą aktów jonizacji, powyżej której komórka nie jest już zdolna do regeneracji. Największą rolę odgrywają tutaj ciężkie cząstki naładowane.
2. Efekty genetyczne - występują przy uszkodzeniach komórek odpowiedzialnych za przekazywanie cech dziedzicznych; przejawiają się one statystycznie w całej populacji.
3. Efekty spowodowane uszkodzeniami radiacyjnymi płodu - uszkadzają embrion we wczesnym stadium rozwoju; wskutek takich uszkodzeń mogą pojawiać się różne zwyrodnienia organizmów."
Większość efektów popromiennych u istot żywych ujawnia się dopiero po pewnym czasie, tzw. okresie utajenia.
"W przypadku komórek somatycznych działają mechanizmy naprawcze, po pewnym czasie uszkodzone cząsteczki mogą zostać usunięte i zastąpione nową cząsteczką. Natomiast fatalne konsekwencje są w przypadku komórek rozrodczych. Skutki modyfikacji są utrwalone. Nie odwracalne. "
Ponadto wyróżniamy skutki stochastyczne i nie stochastyczne promieniowania:
Skutki stochastyczne są skutkami, które pojawiają się na zasadzie przypadkowej i są niezależne od wielkości dawki. Skutek stochastyczny typowo nie ma określonego progu i jest oparty na prawdopodobieństwie, z szansami pojawienia się skutku wraz ze zwiększaniem dawki. Skutkiem stochastycznym oddziaływania promieniowania są nowotwory.
Skutki niestochastyczne są skutkami, które mogą być odniesione bezpośrednio do otrzymanej dawki. Skutek jest bardziej ciężki, gdy dawka jest większa, czyli. oparzenia popromienne są cięższe wraz ze zwiększaniem dawki. Zwykle określa się próg, poniżej którego dany skutek nie występuje. Poparzenie skóry wywołane promieniowaniem jest skutkiem niestochastycznym.
63
Wyszukiwarka
Podobne podstrony:
SHA, Szkoła, Pytania na egzamin inżynierski
Pytania na egzamin inżynierski 52,53
Energetyka 1 pytania na egzamin inżynierski
Pytania na egzamin inżynierski, Semestr 7, Seminarium i praca dyplomowa
Opracowane pytania na egzamin, Inżynieria Środowiska, Migracje Zanieczyszczeń
Stateczność, Szkoła, Pytania na egzamin inżynierski
zestaw pytań obvrona 20.06.02, Szkoła, Pytania na egzamin inżynierski
STATECZNOŚĆ PYTANIA, Szkoła, Pytania na egzamin inżynierski
Nawigacja, Szkoła, Pytania na egzamin inżynierski
SHA, Szkoła, Pytania na egzamin inżynierski
Pytania na egzamin z fizyki, BUDOWNICTWO, Inżynierka, semestr 2, Fizyka
ETIlic 2007 pytania kontrolne na egzamin, Inzynieria Materialowa
Pytania na egzamin - BIOLOGIA, Studia, 1-stopień, inżynierka, Ochrona Środowiska
Fizyka pytania na egzamin
pytania na egzamin fizyka
inzynieria oprogramowania pytania na egzamin dypolmowy, studia, IO
fizyka pytania na egzamin bez 8
Inżynieria oprogramowania Przykładowe pytania na egzamin 4 semestr, edukacja i nauka, Informatyka
więcej podobnych podstron