1. Zasady statyki (aksjomaty)

1. 
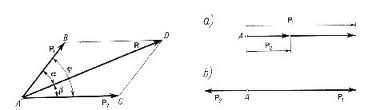
   Zasada równoległoboku: dwie dowolne siły F₁ i F₂ przyłożone do jednego punktu ciała możemy zastąpić siłą wypadkową W przyłożoną do tegoż punktu i przedstawioną jako wektor będący przekątną równoległoboku zbudowanego na wektorach sił składowych F₁ i F₂

2. Zasada równoważenia dwóch sił: dwie siły przyłożone do ciała sztywnego równoważą się tylko wtedy gdy działają wzdłuż jednej prostej, mają przeciwne zwroty oraz te same wartości liczbowe

Często spotykanym przykładem ciała pozostającego w równowadze pod działaniem dwóch sił jest pręt zakończony przegubami na obu końcach, do których przyłożone są siły obciążające. Pręt taki przedstawiony jest na rys. 1.19. Z wyżej wygłoszonej zasady wynika, że siły P i P' w przypadku równowagi muszą działać wzdłuż osi pręta, przy czym P=P'. Gdy siły te działają na pręt tak jak na rys. 1.19a, pręt jest rozciągany, gdy zaś tak jak na rys. 1.19b - ściskany. W rozpatrywanym przypadku założyliśmy, że na pręt przegubowy działają jedynie dwie siły, tzn. pominęliśmy zupełnie jego ciężar.

3. Działanie układu sił przyłożonych do ciała sztywnego nie ulegnie zmianie jeżeli do układu tego dodamy dowolny układ równoważących się sił (tzw. Zerowy)[Uwaga: jedna siła to też układ sił].

Z zasady tej wynika między innymi, że do ciała sztywnego możemy zawsze przyłożyć dwie równe co do wartości liczbowej i przeciwnie skierowane siły, działające wzdłuż jednej linii prostej. Istotnie, siły te bowiem w myśl zasady drugiej równoważą się wzajemnie.
Jako przykład rozpatrzymy ciało, do którego w punkcie A jest przyłożona siła P (rys. 1.20a). Do dowolnego punktu B leżącego na linii działania tej siły przyłożymy dwie równoważące się siły P i P'. Zgodnie z powyższym mamy więc

Przy tym założeniu siły P i P', przyłożone odpowiednio do punktów A i B (rys. 1.20b) rozpatrywanego ciała sztywnego, tworzą także układ dwu równoważących się sił. Zgodnie z zasadą trzecią siły te możemy odrzucić i pozostanie wówczas jedynie siła P przyłożona w punkcie B (rys. 1.20c). Udowodniliśmy więc następujące twierdzenie:
Każdą silę działającą na ciało sztywne można przesuwać dowolnie wzdłuż jej linii działania, Jako punkt przyłożenia siły można obrać więc jakikolwiek punkt leżący na jej Unii działania. Punkt ten może leżeć nawet poza obrębem rozpatrywanego ciała materialnego, gdyż możemy zawsze myślowo związać go niezmiennie z tym ciałem za pomocą układu sztywnych i pozbawionych ciężaru prętów.
Wektor, który może być dowolnie przesuwany wzdłuż prostej, na której leży, nazywa się wektorem posuwnym, w odróżnieniu od wektora związanego z punktem, czyli wektora o początku w ściśle określonym punkcie przestrzeni. Wynika stąd, że wektor przedstawiający siłę działającą na ciało sztywne jest wektorem posuwnym.

4. Zasada zesztywnienia: równowaga sił działających na ciało odkształcalne nie zostanie naruszona przez zesztywnienie tego ciała (zwiększenie sztywności)

Jeśli układ sił działa na ciało o mniejszej sztywności i jest w równowadze to gdy przeniosę ten układ na ciało o większej sztywności to też będzie w równowadze, ale gdy odwrotnie to NIE MUSI tak być. [przykład ze sznurkiem i prętem]

Na podstawie tej zasady może stwierdzić, że warunki równowagi, jakie muszą spełniać siły działające na ciało sztywne, obowiązują również dla ciała odkształcalnego. Jednakże warunki, które w przypadku ciała sztywnego mogą być warunkami wystarczającymi, w przypadku ciała odkształcalnego mogą wymagać uzupełnień zależnych od rodzaju ciała.

5. Zasada działania i przeciwdziałania: każdemu działaniu towarzyszy równe co do wartości i przeciwnie skierowane wzdłuż tej samej prostej przeciwdziałanie.

Jako przykład weźmy jednorodną kulę spoczywającą na poziomej płaszczyźnie (rys. 1.22a). Na kulę tę działa siła ciężkości G oraz siła oddziaływania podłoża, przyłożona w punkcie zetknięcia się kuli z płaszczyzną, tj. w punkcie A. Tę ostatnią siłę oznaczono na rys. 1.22b przez R.

Ponieważ kula znajduje się w spoczynku, siły G i R muszą się równoważyć, a więc działać wzdłuż jednej prostej, jak na rys. 1.22b, i musi być

R=-G

czyli

R=G

W myśl zasady działania i przeciwdziałania kula oddziałuje na podłoże z siłą R' równi co do wartości liczbowej sile R i przeciwnie do niej skierowaną (rys. 1.22c). Mamy więc

R'=-R=G

W przypadku tym siła oddziaływania kuli na podłoże jest równa ciężarowi kuli.
W wyżej rozpatrzonym przykładzie spoczywająca na płaszczyźnie kula poddana była ograniczeniom ruchu i nie mogła zajmować dowolnego położenia w przestrzeni. Takie ograniczenia ruchu ciała nakładane na nie przez inne ciała nazywamy więzami. Siły oddziaływania więzów na podlegające im ciała nazywają się siłami reakcji więzów lub krócej -- reakcjami, dla odróżnienia od sił z góry danych, czyli tzw. sił czynnych. W przykładzie z kulą siłą czynną była siła ciężkości G, reakcją więzów - siła R.
Przy rozpatrywaniu równowagi ciała nieswobodnego będziemy zastępowali oddziaływanie więzów siłami reakcji i następnie traktowali ciało tak jak ciało swobodne. Mówi o tym zasada szósta.

6. Zasada oswobodzenia ciała od więzów: każde ciało nieswobodne można myślowo oswobodzić od więzów zastępując przy tym ich działanie odpowiednimi reakcjami. Dalej ciało takie możemy rozpatrywać jako ciało swobodne podlegające działaniu sił czynnych oraz sił reakcji więzów.

Powyżej zostało powiedziane o podziale sił, na siły czynne i reakcje więzów, teraz natomiast przedstawię jeszcze podział sił na siły zewnętrzne i siły wewnętrzne. Załóżmy, że rozpatrujemy pewien układ składający się z dowolnej liczby ciał materialnych, który nazywać będziemy dalej krótko układem materialnym albo układem mechanicznym.

Otóż siłami zewnętrznymi układu materialnego nazwiemy siły działające na ciała tego układu i stanowiące oddziaływania innych ciał nie należących do niego. Jako siły wewnętrzne natomiast określimy siły wzajemnego oddziaływania na siebie ciał rozpatrywanego układu lub też poszczególnych części jednego ciała. Dla przykładu weźmy układ złożony z Ziemi i Księżyca. Siły oddziaływania Ziemi na Księżyc i odwrotnie są w danym przypadku siłami wewnętrznymi układu, natomiast siły oddziaływania Słońca na te ciała są siłami zewnętrznymi. Jeżeli jednak Słońce zaliczylibyśmy także do naszego układu, to te ostatnie siły należałoby traktować również jako siły wewnętrzne. Z powyższego wynika, że podział na siły wewnętrzne i zewnętrzne jest podziałem względnym i zależy od tego, jaki układ ciał rozpatrujemy.
Weźmy jeszcze inny przykład. Na rysunku 1.23a przedstawiony jest pręt AB rozciągany siłami P i P' przyłożonymi do jego końców i działającymi wzdłuż osi pręta. Zakładając, że pręt pozostaje w równowadze, mamy P=P'. Przetnijmy teraz w myśli rozpatrywany pręt, tak jak zaznaczono na rysunku linią a-a. Aby odcięta część A C pręta znajdowała się w równowadze, należy do wspomnianego przekroju przyłożyć siłę S (rys. 1.23b), stanowiącą oddziaływanie lewej części pręta. Z warunku równowagi dwu sił wynika od razu, że S=P. Siła S jest siłą wewnętrzną, jeżeli chodzi o cały pręt AB, natomiast jest siłą zewnętrzną, jeżeli rozpatrujemy tylko jego część AC. Określoną wyżej siłę wewnętrzną w pręcie nazywamy napięciem. W rozpatrywanym przykładzie mamy do czynienia z napięciem rozciągającym. Jak stwierdziliśmy, napięcie równe jest co do wartości siłom P i P' przyłożonym do końców pręta. Na rysunku 1.23c przedstawiono obie części rozciętego pręta oraz zaznaczono siły, jakie na nie działają. Mamy tu S'=-S.
W ogólnym przypadku, w celu wyznaczenia sił wewnętrznych w jakimś ciele, postępujemy podobnie jak poprzednio, to znaczy rozcinamy myślowo dane ciało i rozpatrujemy równowagę jednej z odciętych części, dla której szukane siły stają się siłami zewnętrznymi. Rozpatrując natomiast całe ciało, nie możemy wyznaczyć w nim sił wewnętrznych, gdyż siły te zgodnie z zasadą działania i przeciwdziałania są zawsze parami równe co do wartości i przeciwnie skierowane, tak że ich działania, jeżeli chodzi o całe ciało, znoszą się wzajemnie.

2. Moment siły względem bieguna. Moment główne układu sił.

Siła przyłożona na pewnym ramieniu to moment.

1. Moment siły względem bieguna.

Momentem siły F względem punktu (bieguna) O nazywamy wektor, którego wartość bezwzględna równa jest iloczynowi wartości liczbowej siły F i ramieniu tej siły względem bieguna O.

Kierunek wektora momentu jest prostopadły do płaszczyzny w której leży linia odkształcenia siły F i bieguna O (do płaszczyzny działania momentu).

Zwrot wektora momentu wynika z reguły śruby o gwincie prawozwojnym lub korkociągu. (Jeżeli siła obraca swoje ramię przeciwnie do obrotu wskazówek zegara to znak jest dodatni)

2. Moment główny układu sił.

Momentem głównym (albo wypadkowym) dowolnego układu sił leżących w jednej płaszczyźnie względem przyjętego bieguna O nazywamy sumę algebraiczną momentów wszystkich sił tego układu względem tego samego bieguna O

3. Wyjaśnić pojęcia: ciało swobodne, ciało nieswobodne, stopnie swobody, więzy, reakcje więzów.

1. Ciało swobodne - jest to takie na które nie działają żadne więzy i może wykonywać dowolny ruch w przestrzeni (6 ruchów, 6 stopni swobody)

2. Ciało nieswobodne - ma mniej niż 6 stopni swobody

3. Stopnie swobody - w fizyce minimalna liczba niezależnych zmiennych opisujących jednoznacznie stan (modelu) układu fizycznego. W praktyce stopień swobody określa liczbę zmiennych układu, które można zmieniać, bez automatycznego powodowania zmian pozostałych zmiennych. (źródło: wikipedia)

4. Więzy - inne ciała, które rozpatrywanemu ciału ograniczają ruch.

5. Reakcje więzów - siły, którymi więzy oddziaływają na ciało. Ich wartość wynika z warunków równowagi.

4. Podać reakcje występujące w najczęściej spotykanych więzach.

1. Więzy z 1 niewiadomą - kierunek siły reakcji jest taki w którym więzy blokują przesunięcie

2. Więzy z 2 niewiadomymi - blokują ruch w dwóch kierunkach

3. Więzy z 3 niewiadomymi - utwierdzenie, zamurowanie

5. Układ sił - definicja. Podział układów sił.

1. Układ sił - Zbiór dowolnej liczby sił jednocześnie działających na ciało nazywamy układem sił

2. Podział układów sił -W zależności od położenia linii działania sił układ możemy

podzielić na dwa rodzaje:
- Układy płaskie
- Układy przestrzenne.
Układ płaski odznacza się tym, że wszystkie siły tworzące ten układ leżą w jednej płaszczyźnie. Układy te możemy podzielić na:
- Układy płaskie zbieżne,
- Układy płaskie równoległe,
- Układy płaskie dowolne.
Układem płaskim zbieżnym nazywamy zbiór ( w jednej płaszczyźnie) sił, których linię działania przecinają się w jednym punkcie.
Układem płaskim równoległym nazywamy zbiór ( w jednej płaszczyźnie) sił, których linie działania są do siebie równoległe. Szczególnym przypadkiem takiego układu są siły działające wzdłuż wspólnej prostej.
Układem płaskim dowolny jest zbiorem (w jednej płaszczyźnie) sił o różnych kierunkach działania.

1. Układ sił leżących na jednej prostej

• Siła wypadkowa

• Warunek równowagi

2. Układy płaskie - wszystkie siły leżą w jednej płaszczyźnie

3. Układy przestrzenne - linie działania wszystkich sił nie leżą w jednej płaszczyźnie)

• Układy płaskie i przestrzenne mogą być:

• Równoległe - linie działania wszystkich sił mają ten sam kierunek

• Zbieżne - linie wypadkowych sił przecinają się w jednym punkcie

• Dowolne - linie działania wszystkich sił układu przecinają się w różnych punktach

6. Podać warunki równowagi dla płaskich układów sił.

1. Aby płaski układ sił był w równowadze wektor główny i moment główny muszą się zerować względem dowolnie dobranego bieguna redukcji.

2. Istnieją 3 algebraiczne warunki równowagi układu płaskiego dowolnego sił.

Aby płaski dowolny układ sił znajdował się w równowadze sumy rzutów wszystkich sił tego układu na dwie wzajemnie prostopadłe osie muszę był równe zeru .

Suma algebraiczna momentów wszystkich sił tego układu względem dowolnego bieguna redukcji O też musi być równa zero.

7. Zdefiniować proste stany obciążenia występujące w wytrzymałości materiałów.

1. Rozciąganie - zachodzi jeżeli na pręt wzdłuż jego osi działa zrównoważony układ sił ze zwrotami na zewnątrz materiału

2. Ściskanie - zachodzi jeżeli na pręt wzdłuż jego osi działa zrównoważony układ sił ze zwrotami do wewnątrz materiału

3. Ścinanie - przypadek obciążenia, w którym układ sił wewnętrznych udaje się sprowadzić do jednej siły działającej w płaszczyźnie przekroju elementu (źródło: wikipedia)

4. Skręcanie - zachodzi jeżeli pasy sił działają prostopadle do osi i ich momenty równoważą się ale działają w przeciwnych kierunkach

5. Zginanie - zachodzi jeżeli momenty leżą w płaszczyźnie XY albo działają siły prostopadłe do podłużnej osi belki

8. Podać i objaśnić prawo Hooke'a przy rozciąganiu.

Odkształcenie jest wprost proporcjonalne do odciążenia i odwrotnie proporcjonalnie do sztywności.

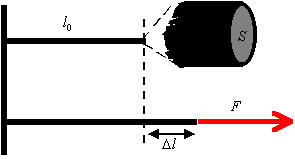
A - pole przekroju

E - moduł Younga

N - siła wewnętrzna

E×A - sztywność rozciągania, ściskania

Im większy moduł Younga tym mniejsze odkształcenie. Moduł Younga zależy on od materiału.

Prawo Hooke'a odnosi się do sytuacji, gdy jakaś siła wywołuje odkształcenie ciała - np. wydłużenie, skrócenie, odchylenie, skręcenie. Prawo Hooke'a odnosi się do najprostszej (jednak często spotykanej w praktyce) sytuacji. Zakładamy tu, że pewna siła odkształcająca (F) wywołuje odkształcenie Δl . W takim przypadku:

Odkształcenie jest wprost proporcjonalne do wywołującej je siły.

Z określenia tego wynika, że jeżeli siła odkształcająca wzrasta dwukrotnie, to i wydłużenie (skrócenie) też będzie dwukrotnie większe; analogicznie przy trzykrotnie większej sile, uzyskamy trzykrotnie większe wydłużenie (skrócenie)m itd. Często jako prawo Hooke'a rozumie się dokładniejsze określenie (wzór) od czego zależy wydłużenie ciała.

Rozpatrzmy przykład pręta, który ma: 

	długość początkową l0,
	pole przekroju poprzecznego S
	i jest rozciągany (lub ściskany siłą F).

 Wtedy wydłużenie   Δl można obliczyć z następującego wzoru:

  Znaczenie symboli:

	l0 - początkowa (bez działania siły) długość pręta (w układzie SI w metrach: m)
	Δl - wydłużenie (ogólnie odkształcenie), czyli zmiana długości pręta (w układzie SI w metrach: N)
	F   - siła powodująca odkształcenie (w układzie SI w niutonach: N = kg·m/s^2)
	S  - pole przekroju poprzecznego (w układzie SI w metrach kwadratowych: m^2)
	K  - współczynnik charakteryzujący materiał (w układzie SI w: m·s^2/kg)

9. Scharakteryzować odkształcenia wzdłużne i poprzeczne rozciąganego (ściskanego) pręta.

1. Pręt rozciągany - zwiększa się długość pręta [delta L >0] , zmniejsza się średnica
   [delta d < 0], E>0, Ep<0. (Wydłużenie i przewężenie)

2. Pręt ściskany - zmniejsza się jego długość [delta L <0], zwiększa średnica[delta d >0], E<0, Ep>0. (Skrócenie i spęczenie)

10. Scharakteryzować stałe sprężystości materiału: E, ν, G

1. E - moduł Younga - moduł odkształcalności liniowej albo moduł sprężystości podłużnej (w układzie jednostek SI) - wielkość określająca sprężystość materiału. Wyraża ona, charakterystyczną dla danego materiału, zależność odkształcenia liniowego ε materiału od naprężenia σ, jakie w nim występuje w zakresie odkształceń sprężystych.

2. ν - liczba Poissona - współczynnik różny dla różnych substancji określający ich zachowanie podczas rozciągania.

3. G - moduł Kirchoffa - współczynnik uzależniający odkształcenie postaciowe materiału od naprężenia, jakie w nim występuje; jest to wielkość określająca sprężystość materiału.

11. Narysować i omówić wykres rozciągania dla materiałów plastycznych.

Typowy wykres naprężenie-odkształcenie pokazuje rysunek. Początkowo wzrost naprężenia powoduje liniowy wzrost odkształcenia. W zakresie tym obowiązuje prawo Hooke'a. Po osiągnięciu naprężenia R_sp, zwanego granicą sprężystości materiał przechodzi w stan plastyczności, a odkształcenie staje się nieodwracalne. Przekroczenie granicy sprężystości, zauważalne w okresie chwilowego braku przyrostu naprężenia, powoduje przejście materiału w stan plastyczny. Dalsze zwiększanie naprężenia powoduje nieliniowy wzrost odkształcenia, aż do momentu wystąpienia zauważalnego, lokalnego przewężenia zwanego szyjką. Naprężenie, w którym pojawia się szyjka, zwane jest wytrzymałością na rozciąganie R_m. Dalsze rozciąganie próbki powoduje jej zerwanie przy naprężeniu rozrywającym R_u.
(Uwaga! Wykres przedstawia dwie linie. Przerywana pokazuje naprężenie rzeczywiste obliczane przy uwzględnieniu przewężenia próbki. Linia ciągła pokazuje wykres naprężenia obliczanego przy uwzględnieniu pola wyjściowego próbki. Czyni się tak, by zaobserwować wartość R_m, będącą lokalnym maksimum krzywej).

12. Wyjaśnić pojęcia: naprężenie dopuszczalne i współczynnik bezpieczeństwa konstrukcji, podać zasady ich wyznaczania.

1. Naprężenie dopuszczalne - naprężenia odpowiadające granicy plastyczności

2. Współczynnik bezpieczeństwa konstrukcji (
   ):

• Zagrożenie jakie może powstać w przypadku zniszczenia konstrukcji

• Czas i warunki pracy konstrukcji

• Dokładność metod obliczeniowych

• 
  

• 
  w prętach

• Naprężenia własne

• Jednorodność materiału

• Dynamika obciążenia

13. Momenty bezwładności (osiowe i biegunowe) figur płaskich - definicja, własności, jednostki.

1. Definicja:

• Osiowy moment bezwładności - jest to suma iloczynów elementarnych pól tej figury Da i kwadratów ich współrzędnej y.

• Biegunowy moment bezwładności - suma dwóch osiowych momentów bezwładności tej figury liczonych względem dwóch wzajemnie prostopadłych osi przecinających się w tym biegunie.

2. Własności:

• Moment bezwładności jest zawsze dodatni

• Wielkość momentu bezwładności zależy od położenia

3. Jednostka:
   - jednostka długości do 4 potęgi

14. Podać i zilustrować przykładem twierdzenie Steinera.

Moment bezwładności figury względem osi X równoległej do osi środkowej x₀ jest równy momentowi bezwładności tej figury względem osi x₀ powiększonemu o iloczyn pola tej figury i kwadratu współrzędnej y_c (odległości między osiami X i x₀)

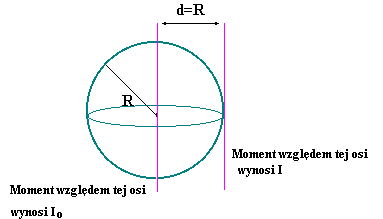
Twierdzenie Steinera - przykład.

Na rysunku przedstawiono układ dwóch jednakowych mas równych 5 kg. Korzystając z Twierdzenia Steinera znajdź moment bezwładności względem osi przechodzącej przez jedną z mas. Odległość pomiędzy masami wynosi 2m.

Aby znaleźć moment bezwładności względem osi przechodzącej przez jedną z mas należy najpierw wyznaczyć moment bezwładności względem środka masy:

Wstawiając ten wynik do wzoru na Twierdzenie Steinera otrzymamy:

15. Skręcanie prętów o przekroju kołowym - założenia, odkształcenia, rozkład naprężeń w przekroju (wykres i wzór z objaśnieniem).

1. Założenia:

1. Przekroje poprzeczne kołowe przed odkształceniem pozostają kołowymi również po odkształceniu doznając jedynie obrotu wokół pręta.

2. Promień przekroju obraca się wraz z całym przekrojem pozostając prostoliniowym.

3. Linie tworzące pręta nie zmieniają swej długości

2. Odkształcenia: Występują odkształcenia postaciowe (nie zmienia się długość tylko postać) wywołane naprężeniami stycznymi, czyli naprężeniami wzdłuż ścianek. ( Taki efekt przy skręcaniu, jeden przekrój względem drugiego jest ścinany.)

3. Rozkład naprężeń w przekroju: Przy skręcaniu prętów o przekroju kołowym nie ma zmiany długości, nie ma naprężeń prostopadłych, są naprężenia styczne.

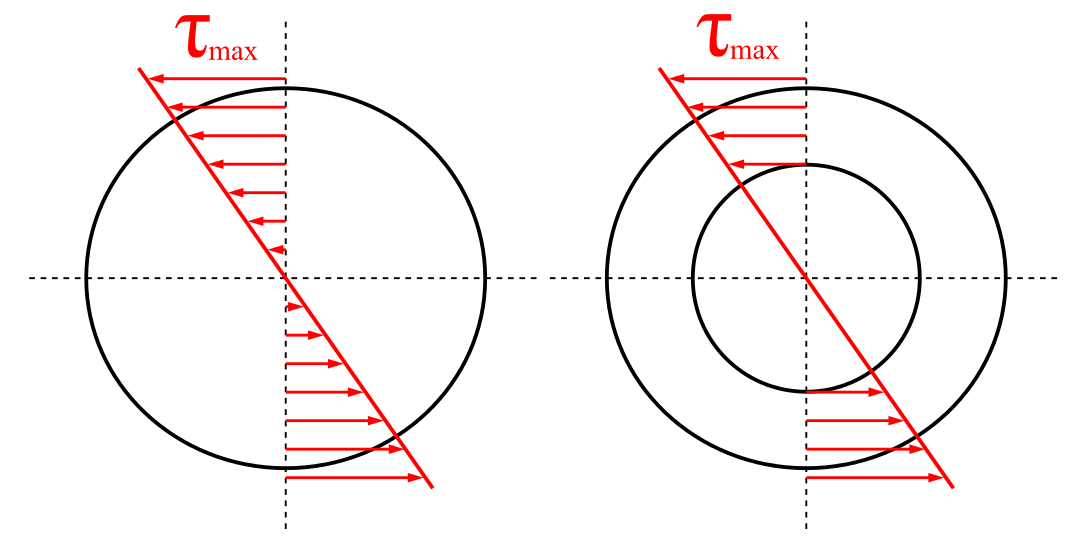
19. Podać warunek wytrzymałościowy na skręcanie, omówić sposoby korzystania z niego.

1. Warunek wytrzymałościowy na skręcanie

gdzie:
t_s - naprężenia styczne skręcające w [Pa],
M - moment skręcający przekrój  w [Nm],
W_o - wskaźnik wytrzymałości przekroju na skręcanie [m³],

k_s - naprężenia dopuszczalne na skręcanie w [Pa]

2. Sposoby korzystania:

• Dla przekroju kołowego pełnego

• Dla przekroju kołowego drążonego

20. Podać i omówić wzór na kąt skręcenia przekroju kołowego pręta. Wyjaśnić co to jest sztywność skręcania.

1. Wzór na kąt skręcenia

gdzie:

M - moment skręcający przekrój

L - długość pręta

G - moduł Kirchoffa

J₀ - moment bezwładności

2. Sztywność skręcania : iloczyn modułu Kirchhoffa i momentu bezwładności na skręcanie

21. Wymienić rodzaje zginanych belek, omówić odkształcenia podłużnych włókien, rozkład naprężeń normalnych w przekroju belki (wykres i wzór z objaśnieniem).

1. Rodzaje zginanych belek:

W statyce, w zależności od sposobu podparcia, rozróżniamy belki:

belki statycznie wyznaczalne, czyli takie, w których liczba niewiadomych reakcji jest równa liczbie równań równowagi:

belki jednoprzęsłowe swobodnie podparte (trzy reakcje podporowe i trzy równania równowagi);

belki utwierdzone (wsporniki) zamocowane sztywno na jednym z końców, a na drugim swobodne;

belki ciągłe (wieloprzęsłowe) przegubowe, czyli belki podparte w taki sposób, że jedna z podpór należy do nieprzesuwnych, a pozostałe do przesuwnych (łożysko umożliwiające przesuw belki wzdłuż jej osi). Dodatkowo, dla zapewnienia statycznej wyznaczalności układu, wprowadza się odpowiednią liczbę przegubów w jej przęsłach. Sposób umiejscowienia przegubów nie może wprowadzić geometrycznej zmienności układu. (Na każdej podporze przesuwnej występuje jedna reakcja podporowa, na nieprzesuwnej - dwie. Stąd dla belki podpartej na „n” podporach mamy n+1 nieznanych reakcji podporowych. Przy belce ciągłej, bez przegubów, mamy do dyspozycji trzy równania równowagi, zatem stopień statycznej niewyznaczalności belki można określić jako n-2. Aby układ był statycznie wyznaczalny należy wprowadzić n-2 przeguby).

belki statycznie niewyznaczalne (siły w nich występujące nie dają się wyliczyć wyłącznie przy pomocy równań równowagi):

belki jednoprzęsłowe utwierdzone na końcach (każde utwierdzenie to trzy reakcje podporowe, zatem przy dwustronnym utwierdzeniu układ jest trzykrotnie statyczne niewyznaczalny), utwierdzone na jednym z końców i podparte przesuwnie lub nieprzesuwnie na drugim albo podparte z dwóch stron w sposób nieprzesuwny;

belki wieloprzęsłowe bez przegubów albo z przegubami w ilości mniejszej niż konieczna dla zapewnienia statycznej wyznaczalności układu.

2. Odkształcenia podłużnych włókien:

Doświadczenia przeprowadzone ze zginanymi prętami pokazują, że:
- włókna górne uległy skróceniu (rys. 2.19a) w przekroju wzdłużnym, zaś w tej części w przekroju poprzecznym pręt poszerzy się (rys. 2.19b),
- włókna dolne uległy wydłużeniu i odpowiednio zwężeniu,
- względne odkształcenia poprzeczne pręta w każdym punkcie są proporcjonalne (poprzez liczbę Poissona n ) do odkształceń wzdłużnych a więc istnieje związek między odkształceniami podobnie jak przy rozciąganiu lub ściskaniu,
- włókna równoległe do osi pręta znajdują się w jednokierunkowym stanie naprężeń (rozciąganie lub ściskanie) i nie wywierają na siebie żadnych nacisków poprzecznych,
- w strefie środkowej (warstwa obojętna) odkształcenia i naprężenia są równe zeru.

3. Rozkład naprężeń normalnych w przekroju belki:
   Naprężenia normalne w warstwie odległej o y od warstwy obojętnej:

J_z - osiowy moment bezwładności przekroju porzecznego belki.

22. Wyjaśnić jakie obciążenia wewnętrzne występują w przekrojach zginanych belek, podać ich definicje i umowy dotyczące znaków.

1. Siła poprzeczna w dowolnym przekroju równoważny siły zewnętrzne po jednej stronie tegoż przekroju. Siła poprzeczna jest więc suma (z odpowiednim znakiem) siłą prostopadłą do osi belki działającą na jedną płaszczyznę.

2. Przy wyznaczaniu siły poprzecznej w przekroju belki ze znakiem + uwzględniamy te siły zewnętrzne, które dążą do obrotu rozpatrywanej części belki w stronę zgodną z Rychem wskazówek zegara, zaś ze znakiem -uwzględniamy te siły zewnętrzne, które dążą do obrotu w stronę przeciwną.

3. Moment zginający w dowolnym przekroju równoważy moment sił zewnętrznych po jednej stronie tegoż przekroju. Moment zginający w rozpatrywanym przekroju belki jest zatem algebraiczną sumą wszystkich momentów tworzonych przez obciążenia zewnętrzn, działające na rozpatrywaną belkę.

• Belka zginana „wypukłością w dół” () - dodatnie siły wewnętrzne.

• Belka zginana „wypukłością w górę”() - ujemne siły wewnętrzne.

23. Wyjaśnić co to jest przekrój niebezpieczny belki, podać i objaśnić warunek wytrzymałościowy na zginanie, omówić sposoby korzystania z niego.

1. Na przekroje niebezpieczne wskazują maksymalne wartości momentu zginającego

2. Warunek wytrzymałościowy na zginanie

σ_gmax- naprężenia normalne zginające w [Pa],
M_gmax - moment zginający przekrój  w [Nm],
W_z - wskaźnik wytrzymałości przekroju na zginanie [m³],
k_g - naprężenia dopuszczalne na zginanie w [Pa]

3. Sposoby korzystania:

• Dla przekroju prostokątnego pełnego

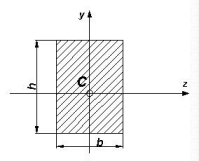
• Dla przekroju kołowego pełnego

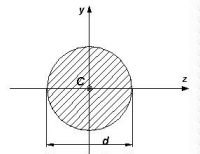
• Dla pręta prostokątnego drążonego

---