Stopa nominalna
Utarło się, iż stopy procentowe podaje się w wartościach nominalnych, w domyśle rocznych (ang. − Annual Percentage Rate − APR). Stopa nominalna rNom jest to
rNom =![]()
, gdzie (1.12)
PV − wartość kapitału na początku roku,
FV − wartość kapitału na końcu roku,
oraz okres kapitalizacji jest równy 1 rok.
Jest przyjęte, że oprocentowanie za jeden okres kapitalizacji tkap ustala się ze wzoru:
![]()
, gdzie (1.13)
tkap − czas okresu kapitalizacji
t1rok − czas jednego roku.
Stąd jeżeli liczba okresów kapitalizacji w ciągu roku jest liczbą całkowitą m, to
![]()
co po podstawieniu do wzoru 1.13 daje (1.14)
![]()
. (1.15)
W zakresie ustalenia długości roku na świecie stosuje się różne ustalenia. W niektórych krajach istnieje dowolność i umowa definiuje długość roku, banki ustalają tę długość na
360 dni lub
365 dni lub
rzeczywistą długość roku kalendarzowego.
W Polsce, po okresie panowania dowolności w tym zakresie, został ustalony
dla depozytów bankowych rok rzeczywisty,
dla kredytów bankowych zgodnie z umową kredytową,
dla obligacji rok rzeczywisty,
dla bonów skarbowych rok 360 dniowy.
Stopa efektywna
Stopą efektywną nazywa się wielkość
Stopa efektywna=![]()
, gdzie
PV − wartość kapitału na początku okresu, dla którego jest liczona stopa efektywna,
FV − wartość kapitału na końcu okresu, dla którego jest liczona stopa efektywna,
oraz okres kapitalizacji jest dowolny, czym różni się ta definicja od definicji stopy nominalnej.
Stopy efektywnej używa się raczej rzadko, ponieważ przy porównywaniu stóp procentowych należy porównywać oprocentowania za ten sam okres.
Z tego powodu wprowadzono często używane pojęcie rocznej stopy efektywnej (ang. Effective Annual Rate − EFF).
![]()
, gdzie
PV − wartość kapitału na początku roku,
FV − wartość kapitału na końcu roku,
oraz okres kapitalizacji jest dowolny.
Jeżeli liczba kapitalizacji w ciągu roku jest równa m, to ze wzoru 1.5 dla czasu jednego roku równego m okresom kapitalizacji i ![]()
mamy

, czyli
![]()
(1.16)
Zawsze zachodzi nierówność
![]()
, ponieważ (1.17)
![]()
,
![]()
![]()
co jest oczywiste jeśli tylko rNom > 0.
Wynika z tego, że kapitalizacja częstsza niż 1 rok zwiększa efektywność oprocentowania i to tym bardziej im większe jest m:
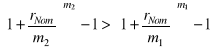
, jeśli m2 > m1 oraz rNom > 0
Zamiast więc stosowania kapitalizacji częstszej niż roczna można używać stopy efektywnej i kapitalizacji rocznej.
W przypadku gdy stopy oprocentowania w poszczególnych okresach kapitalizacji są różne, to oczywiście
![]()
czyli
![]()
.
Można wyprowadzić wzór na wartość przyszłą FV dla n lat i m okresów kapitalizacji. Liczba okresów kapitalizacji w ciągu n lat będzie równa n*m, co po podstawieniu do wzoru 1.5 daje
![]()
, a ponieważ ![]()
, więc wzór ostatecznie przyjmie postać
![]()
, gdzie (1.18)
m − liczba kapitalizacji w ciągu roku,
n − liczba lat, a nie jak we wzorze 1.5 liczba okresów.
rNom − oprocentowanie nominalne.
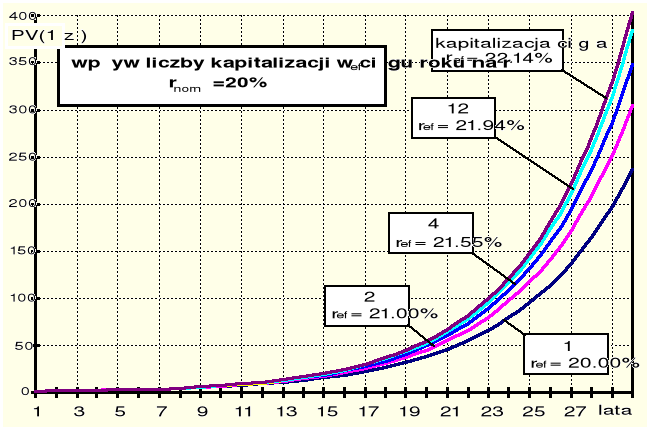
Rys. 1.6. Wpływ częstości kapitalizacji w ciągu roku na wartość przyszłą 1 zł.
Wnioski
Wniosek A
Z rozważań przeprowadzonych dotąd w niniejszym rozdziale wynika mnemotechniczna zasada pozwalająca często uprościć obliczenia.
Dowolny pojedynczy przepływ pieniądza można dowolnie przesunąć w czasie, czyli zastąpić go innym wpływem lub wypływem w innym czasie o ile wielkość tego sztucznie powstałego przepływu zostanie ustalona zgodnie z teorią wartości pieniądza w czasie.
A więc jeśli przepływ zostanie przesunięty do tyłu (w kierunku zera osi czasu), należy zastąpić go jego wartością obecną.. Jeśli przepływ zostanie przesunięty w czasie do przodu, należy go zastąpić jego wartością przyszłą.
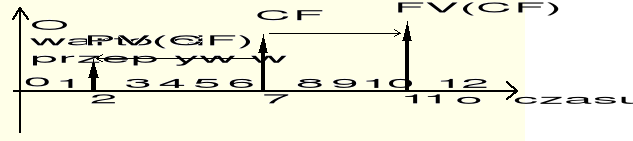
Rys. 1.7. Dowolny przepływ CF można przesunąć w czasie zastępując go jego wartością obecną lub przyszłą odpowiednio.
Wniosek B
Jeśli wartość A jest X razy większa od wartości B to przy tym samym oprocentowaniu r i tej samej liczbie okresów n wartość przyszła FV(A) jest X razy większa od wartości przyszłej FV(B):
FV(A) = A*(1 + r)n =X*B*(1 + r)n = X*[B*(1 + r)n ]= X*FV(B). (1.19B)
Wniosek C
Analogicznie można pokazać, że
jeśli wartość A jest X razy większa od wartości B to przy tym samym oprocentowaniu r i tej samej liczbie okresów n wartość obecna PV(A) jest X razy większa od wartości obecnej PV(B):
![]()
(1.19C)
Realna stopa zwrotu
Przykład 1.5.
Mr. Kowalsky prowadzi firmę w Stanach Zjednoczonych. Przynosi mu ona 25% zwrotu z wniesionego do firmy kapitału. Ponieważ dowiedział się, że Polsce można osiągnąć duży zwrot z zainwestowanego kapitału, a posiada jeszcze sporo wolnej gotówki postanowił zainwestować w Polsce. W tym celu założył w Polsce firmę Kowalsky & Son, 7 maja 1999 r. wymienił 1 mln dolarów na złotówki po kursie 3,889zł/USD a uzyskane złotówki zainwestował w produkcję.
Ponieważ prowadzenie dwu firm, jednej w Stanach Zjednoczonych, drugiej w Polsce okazało się zbyt trudne, po roku zrezygnował z działalności w Polsce i 07 maja 2000 r. sprzedał firmę. Uzyskał zwrot z inwestycji 45%, a firmę udało mu się sprzedać za równowartość inwestycji, to znaczy za 3,889 mln zł.
Uzyskane złotówki wymienił na dolary po aktualnym kursie. Okazało się, że w ciągu roku inflacja złotówki do dolara wyniosła 20%.
Ile wyniosła wartość przyszła kapitału 1 mln USD po roku inwestycji w Polsce oraz jaki to stanowi zwrot z inwestycji? Dla uproszczenia, w przykładzie przyjęto kursy średnie zamiast osobnych kursów sprzedaży i kupna USD.
Oznaczmy przez:
rzł = 45% - stopa zwrotu z inwestycji w Polsce,
r$ - poszukiwana stopa zwrotu w USD z inwestycji w Polsce,
PV$ = 1 000 000 USD - wielkość inwestycji,
PVzł - wielkość inwestycji w złotych,
FVzł kwota w złotych uzyskana z inwestycji (łącznie z wycofanym kapitałem),
FV$ = kwota w USD uzyskana z inwestycji (łącznie z wycofanym kapitałem),
rinf zł/$ = 20% - inflacja USD do złotego,
k1 - kurs złotego do USD 7 maja 1999 r,
k2 - kurs złotego do USD 7 maja 2000 r.
Po roku pan Kowalsky uzyskał kapitał z wymiany kapitału w złotych na kapitał w USD:
![]()
.
Ale kapitał w złotych uzyskał ze zwrotu z inwestycji, który wyniósł rzł = 45%:
![]()
, natomiast kurs wymiany k2 uzyskamy ze stopy inflacji złotówki do USD:
![]()
i otrzymamy
![]()
.
Natomiast kapitał początkowy w złotych PVzł uzyskał z kapitału początkowego w dolarach PV$ po kursie wymiany k1:
![]()
, czyli
![]()
.
Ze wzoru widać, że wpływ czynnika niekorzystnego (inflacji złotówki do dolara) wpływa poprzez czynnik (1 +stopa procentowa przeciwdziałająca wzrostowi kapitału) ale w mianowniku.
Ponieważ
![]()
więc
![]()
i wstawiając za FV$ prawą stronę poprzedniego wzoru i skracając przez PV$ mamy wzór na stopę zwrotu w USD:
![]()
.
Przykład 1.6.
Gdyby kwotę PV została ulokowana w banku przy stopie procentowej r z zamiarem utrzymania lokaty przez n okresów kapitalizacji, to wartość kapitału po n okresach wyniosłaby
![]()
.
Ale gdyby depozytariusz zdecydował się ją z jakiś powodów wycofać o jeden okres wcześniej, to otrzymałby kwotę
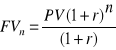
A więc i w tym przypadku wpływ czynnika niekorzystnego (skrócenie okresu depozytu) wpływa poprzez podzielenie przez czynnik (1 +stopa procentowa przeciwdziałająca wzrostowi kapitału).
Oba przykłady prowadzą do wniosku, który można wyrazić wzorem:
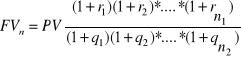
, gdzie
![]()
są stopami oprocentowania za kolejne okresy, których jest n1,
![]()
są stopami procentowymi n2 czynników wpływających negatywnie na wzrost kapitału.
W szczególności ![]()
mogą być stopami inflacji. Wówczas powinno się uwzględnić ich tyle ile okresów kapitalizacji oraz można je oznaczyć wspólną literą n, ![]()
.
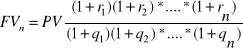
. (1.20a)
Stopę zwrotu z kapitału, uwzględniającą wpływ inflacji nazywa się stopą realną.
Stopę realną definiuje się podobnie do stopy efektywnej, z tym że uwzględnia ona dodatkowo wpływ inflacji:
![]()
.
Stąd można wyprowadzić wzór na stopę realną dla n okresów, w każdym okresie oprocentowanie wynosi ri, stopa inflacji qi:
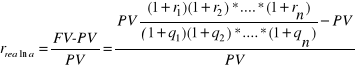
, czyli
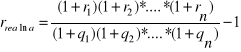
(1.20b)
Jeśli stopa realna ma być roczną stopą realną, oczywiście wszystkie okresy kapitalizacji muszą łącznie stanowić dokładnie jeden rok.
Przykład 1.7.
Jeśli nominalna stopa oprocentowania kredytu wynosi rNom, = 24%, inflacja roczna wynosi q = 10%, to przy spłacie kredytu jeden raz w roku realny koszt kredytu wynosi
![]()
Gdyby spłaty następowały miesięcznie, a inflacja każdego miesiąca wynosiła q' = 1%, to
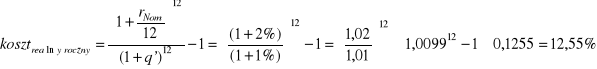
Kapitalizacja ciągła
W teorii finansów wykorzystywane jest pojęcie kapitalizacji ciągłej. W tej książce będzie to pojęcie wykorzystywane na przykład przy analizie opcji. Okres kapitalizacji ciągłej to granica coraz krótszych okresów kapitalizacji: roku, miesiąca, tygodnia, dnia, sekundy, mikrosekundy itd. W granicy uzyskamy odcinek czasu o zerowej długości. Oprocentowanie efektywne przy kapitalizacji ciągłej ref,c uzyskujemy ze wzoru 1.16, przechodząc z liczbą kapitalizacji m w ciągu roku do nieskończoności:
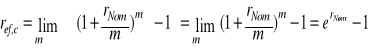
, (1.21)
gdzie liczba e ≈ 2,718 jest podstawą logarytmów naturalnych.
**************
Rozważmy najpierw sytuację inwestora długoterminowego kupującego akcje z zamiarem trzymania ich w nieskończoność - oczekującego dochodu tylko w formie wypłacanych mu corocznie dywidend. W tej sytuacji wychodząc z określenia ceny akcji P0 jako nieskończonej sumy zdyskontowanych dywidend (6.3) i podstawiając za Dt wyrażenie (6.6) otrzymuje się
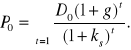
(1.7)
Oznaczmy
![]()
(1.8)
Jeśli ks > g, to 1+h< 1 i wówczas wykorzystując wzór na sumę skumulowanych strumieni gotówki otrzymujemy
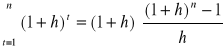
. (1.9)
Granica (6.9) przy n wynosi
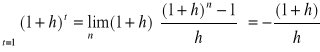
. (1.10)
Biorąc pod uwagę wyrażenie (6.8), otrzymujemy
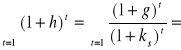
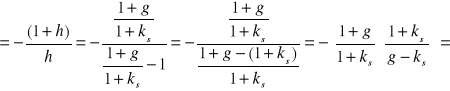
![]()
(1.11)
Wstawiając teraz wyrażenie (6.10) do (6.11), otrzymujemy
![]()
(1.12)
Zatem cena akcji, jaką potencjalny inwestor jest skłonny zapłacić w chwili t = 0 przy żądanej stopie zwrotu ks i prognozowanej stopie wzrostu firmy g jest równa stosunkowi oczekiwanej dywidendy roku przyszłego t = 1 oraz różnicy między żądaną stopą zwrotu i stopą wzrostu firmy. Ma więc wartość renty wiecznej o płatności rocznej D1 i stopie dyskontowej r = ks - gs, czyli mniejszej o g od żądanej stopy zwrotu ks.
Należy podkreślić, że wyrażenie (6.12) jest słuszne wtedy i tylko wtedy, gdy ks > g;
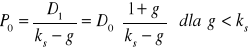
W przypadku ks * g wyrażenie (6.11) traci sens, ponieważ jest ono słuszne tylko w tym przypadku, gdy zachodzi (6.9).
Dla g = ks, tzn. gdy stopa wzrostu i żądana stopa zwrotu akcjonariusza są sobie równe zachodzi
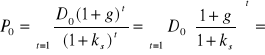
![]()
Analogicznie w przypadku, gdy g > ks;
ponieważ g > ks, a więc 1 + g > 1 + ks oraz h > 0, stąd
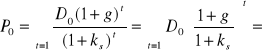
![]()
.
W sytuacji, gdy inwestor kupuje akcje z zamiarem sprzedania ich po upływie n lat, cena akcji P0, jaką jest on skłonny zapłacić w chwili t = 0 przy żądanej stopie zwrotu ks oraz stopie wzrostu firmy (w sensie zysku netto i dywidendy) g < ks, zgodnie ze wzorem (6.2) oraz (6.12) wynosi
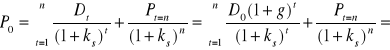
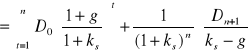
, (1.13)
albo przy oznaczeniu ![]()
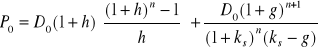
, (1.14)
czyli składa się z dwu składników
- skończonej sumy zdyskontowanych strumieni dywidend z n okresów oraz
- zdyskontowanej (stopa dyskontowa jest równa ks) przez n okresów oczekiwanej ceny akcji w chwili t = n, która zgodnie z (6.12) wynosi
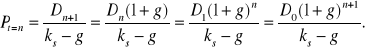
, dla g < ks. (1.15)
Jeżeli stopa wzrostu g ![]()
ks, zachodzi:
dla g = ks
![]()
![]()
dla g > ks
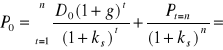
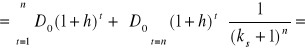
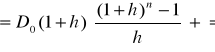
W obu przypadkach, inwestycji długoterminowych i krótkoterminowych, w sytuacji gdy
przewidywana stopa wzrostu firmy jest stała i
inwestor godzi się zarobić mniej, niż prognozowany poziom stopy wzrostu firmy ks < g, a
z polityki firmy dotyczącej wypłaty dywidend wynika, że udział wypłaconych dywidend w zysku netto jest stały,

= const;
cena akcji P0 jaką może zapłacić potencjalny inwestor wynika tylko z kompromisu będącego wynikiem negocjacji między sprzedającym i kupującym. Z rozważanego modelu dywidendowego wynika bowiem, że cena akcji powinna być nieskończenie wysoka, co oczywiście w praktyce jest sytuacją nierealną.
W sytuacji, gdy stopa wzrostu firmy przekracza żądaną stopę zwrotu inwestora, g1>ks, ale tylko w początkowym okresie dla t![]()
{1,2,..., n}, czyli od momentu zakupienia akcji aż do chwili t = n, a następnie przewiduje się stałą stopę wzrostu g2<ks, to cenę akcji można wyznaczyć w następujący sposób:
zgodnie z (6.12)
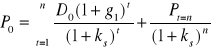
,
cenę akcji w przypadku, gdy g < ks zgodnie ze wzorem (6.12) wyznacza się jako ![]()
. Zatem można napisać, że ![]()
. Ponieważ Dn+1 = Dn(1+g), a w rozważanym przypadku do momentu t = n stopa wzrostu wynosi g1, a w okresie t = n+1 obowiązuje już stopa wzrostu g2, to Dn+1 = Dn(1+g2), gdzie Dn = D0(1+g1).
Stąd
![]()
Zatem
![]()
. (1.16)
W podobny sposób wyznaczyć można cenę akcji P0 w sytuacji, gdy inwestor rozważa zakup akcji o nierównomiernie zmieniającej się stopie wzrostu firmy, przy założeniu jednak, że końcowa stopu wzrostu będzie stała i mniejsza od żądanej stopy zwrotu akcjonariusza.
Rozważając stopę wzrostu firmy (w sensie wzrostu zysku netto) rozważa się następujące sytuacje
1. malejący zysk netto firmy, stopa wzrostu g < 0,
2. zerowy wzrost firmy (zysk netto = constans), stopa wzrostu g = 0,
3. stały lub normalny wzrost firmy, stopa wzrostu g > 0, ale g < ks,
4. supernormalny wzrost firmy, stopa wzrostu gs > 0, rzędu kilkunastu procent rocznie, ale gs < ks,
5. niestały wzrost firmy: supernormalny wzrost w początkowym skończonym okresie, stopa wzrostu gs niekoniecznie musi być mniejsze od stopy ks, a następnie wzrost normalny gn < gs i z warunkiem gn < ks,.
Prawo bankowe, Art. 53. Środki pieniężne na rachunku bankowym mogą być oprocentowane według stopy stałej lub zmiennej w wysokości i na zasadach określonych w umowie. Do obliczania odsetek przyjmuje się, że miesiąc liczy 30 dni, a rok 365 dni.
6
9
Wyszukiwarka
Podobne podstrony:
materialy do wykladu dla Polit, Zarządzanie PWr, III semestr, Rachunkowość finansowa
dudycz, PWR, Zarządzanie, SEMESTR IV, Finanse przedsiębiorstw
1 kolo - opracowaniej, Zarządzanie PWR, Semestr 6, Analiza finansowa wspomagana komputerem
1. ZARZĄDZANIE FINANSAMI PRZEDSIĘBIORSTW, PWR, Zarządzanie, SEMESTR V, Zarządzanie finansami
ZRODLA-F, PWR, Zarządzanie, SEMESTR V, Zarządzanie finansami
kolo 2-sc, Zarządzanie PWR, Semestr 6, Analiza finansowa wspomagana komputerem
ściąga - finanse przedsiębiorstw, Studia Zarządzanie PWR, Zarządzanie PWR I Stopień, IV Semestr, Fin
1.1.1.1 Wartość przyszła renty, PWR, Zarządzanie, SEMESTR V, Zarządzanie finansami
finanseprzedsiebiorstw., Studia Zarządzanie PWR, Zarządzanie PWR I Stopień, IV Semestr, Finanse prze
EGZAMIN ZAGADNIENIA, PWR, Zarządzanie, SEMESTR IV, Finanse przedsiębiorstw
4. RYZYKO, PWR, Zarządzanie, SEMESTR V, Zarządzanie finansami
ZADANIA EGZAMINACYJNE finanse przedsiebiorstw, Studia Zarządzanie PWR, Zarządzanie PWR I Stopień, IV
kolo 2, Zarządzanie PWR, Semestr 6, Analiza finansowa wspomagana komputerem
BM TEST, PWR, Zarządzanie, SEMESTR V, Badania marketingowe
opracowane pytania MSI (1), Studia Zarządzanie PWR, Zarządzanie PWR I Stopień, V Semestr, Modelowani
Wykład 3 Zarządzanie finansami Rachunek zysków, Notatki UTP - Zarządzanie, Semestr IV, Zarządzanie f
podanie rodzica dziecka zameldowanego i zamieszkalego p, PWR, Zarządzanie, SEMESTR IV, Metody badani
więcej podobnych podstron