Sprawozdanie pobrane ze StudentSite.pl |
|
Chcesz więcej? Wejdź na: http://www.studentsite.pl/materialy_studenckie.html |
|
Możesz także wspomóc swoimi sprawozdaniami innych: http://www.studentsite.pl/panel_materialy_studenckie/add |
|

Politechnika Śląska
Instytut Fizyki
Pracownia Fizyczna
LABORATORIUM Z FIZYKI
Temat ćwiczenia: Wyznaczanie przyśpieszenia ziemskiego za pomocą wahadła rewersyjnego.
Wydział: Elektryczny Kierunek: Elektronika i telekomunikacja
Grupa: Rok akademicki: 2009/2010
Sekcja:
Data:
|
Ocena końcowa: |
Podpis przyjmującego: |
Wprowadzenie.
Celem ćwiczenia jest wyznaczenie przyśpieszenia ziemskiego. Przy założeniu braku sił oporu powietrza, wartość tego przyspieszenia przy powierzchni Ziemi wynosi:
![]()
( 1 )
gdzie ![]()
- siła grawitacji,![]()
- masa ziemi, ![]()
- promień Ziemi.
Przyspieszenie ziemskie ![]()
maleje ze wzrostem wysokości. Dochodzimy zatem do wniosku, że przyspieszenie ziemskie powinniśmy wyznaczać metodami doświadczalnymi.
Najprostszą metodą pomiaru przyspieszenia ziemskiego wydaje się sposób pomiaru czasu spadku swobodnego. Nie daje on jednak wystarczająco zadawalających wyników z powodu konieczności uwzględniania np. opór powietrza. My wyznaczamy przyspieszenie ziemskie za pomocą wahadła rewersyjnego.
WAHADŁO REWERSYJNE
Wahadłem fizycznym jest bryła sztywna wykonująca wahania wokół osi poziomej zawieszenia, ulokowanej powyżej środka ciężkości. Na bryłę wychyloną z położenia równowagi o kąt działa moment obrotowy:
![]()
( 2 )
We wzorze tym ![]()
jest odległością środka ciężkości od punktu zawieszenia. Równanie ruchu wynosi:
![]()
( 3 )
gdzie ![]()
- moment bezwładności, ![]()
- przyśpieszeniem kątowym. Dla małych kątów sinus można zastąpić wartością kąta w mierze łukowej. Drgania wahadła fizycznego są w przybliżeniu harmoniczne o okresie:
![]()
( 4 )
Wzór ten jednak nie pozwala na wyznaczenie przyśpieszenia ziemskiego ze względu na kłopotliwy sposób określania zarówno momentu bezwładności, jak i odległości ![]()
. Problemów tych unikamy stosując tzw. wahadło rewersyjne, które jest rodzajem wahadła fizycznego o dwóch równoległych osiach zawieszenia i regulowanym rozkładzie masy. Dzięki czemu możliwe jest osiągnięcie identycznych okresów drgań przy obu sposobach zawieszenia. Pozwala to na precyzyjne wyznaczenie wartości przyspieszenia grawitacyjnego w badanym miejscu.
Zasada pomiaru.
Wahadło rewersyjne złożone jest z pręta, dwóch pierścieni z nacięciami z nacięciami i dwóch ciężarków. Jeden z ciężarków jest zamocowany jako nieruchomo, drugi może być przesuwany wzdłuż osi wahadła. Zmiana położenia ciężarka powoduje zmianę usytuowania środka ciężkości oraz zmianę momentu bezwładności ![]()
. Pociąga to za sobą zmianę okresu drgań. Dla drugiego zawieszenia sytuacja jest analogiczna. Zasada wyznaczania przyśpieszenia ziemskiego sprowadza się do znalezienia takiego położenia ruchomego ciężarka , które odpowiada jednakowym okresom drgań dla obydwu zawieszeń wahadła rewersyjnego. Procedura dochodzenia do stanu odwracalności wahadła realizowana jest w etapach:
zmiana odległości
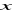
co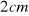
i pomiar okresu drgań dla obu zawieszeń,sporządzenie wykresu i przybliżone oszacowanie położenia odwracalnego na podstawie przecięcia parabol,
precyzyjne wyznaczenie okresu drgań odpowiadającemu warunkowi odwracalności
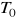
.
Przyśpieszenie ziemskie obliczamy wg wzoru:
![]()
, ( 5 )
gdzie ![]()
- jest odległością między zawieszeniami.
Przebieg ćwiczenia.
Zmierzyliśmy odległość między ostrzami wahadła.
Zawiesiliśmy wahadło na ostrzu zamocowanym na końcu pręta (ostrze A).
Wprawiliśmy wahadło w ruch i zmierzyliśmy czas 10 okresów (kąt wychylenia nie powinien być większy niż
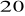
).Zawiesiliśmy wahadło na drugim ostrzu i ponownie zmierzono czas 10 okresów.
Wykonaliśmy czynności opisane wyżej dla położeń ciężarka zmienianego co
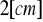
.Dane zamieściliśmy w Tabela 1.Po umieszczeniu danych na wykresie zależności okresu wahań od odległości ciężarka od ostrza A (dla obydwu sposobów zawieszenia). Z Wykresu 1 określiliśmy położenie ciężarka, przy którym okresy drgań są jednakowe dla obu zawieszeń.
Obliczyliśmy przyśpieszenie ziemskie wg wzoru ( 5 ).
Przeprowadziliśmy rachunek błędów.
Pomiary i obliczenia.
Ilość okresów: N=10.
Odległość między ostrzami: 46,6[cm]
Tabela 1 Zależność okresu T [s] od położenia ciężarka x [cm] dla ostrza A i ostrza B
Położenie |
Ostrze A |
Ostrze B |
||
|
czas 10 okresów |
okres T |
czas 10 okresów |
okres T |
2 |
13,630 |
1,363 |
13,657 |
1,366 |
4 |
13,384 |
1,338 |
13,482 |
1,348 |
6 |
13,118 |
1,312 |
13,333 |
1,333 |
8 |
12,868 |
1,287 |
13,220 |
1,322 |
10 |
12,624 |
1,262 |
13,118 |
1,312 |
12 |
12,365 |
1,237 |
13,035 |
1,304 |
14 |
12,117 |
1,212 |
12,978 |
1,298 |
16 |
11,870 |
1,187 |
12,989 |
1,299 |
18 |
11,635 |
1,164 |
12,922 |
1,292 |
20 |
11,400 |
1,140 |
12,916 |
1,292 |
22 |
11,169 |
1,117 |
12,936 |
1,294 |
24 |
10,966 |
1,097 |
12,945 |
1,295 |
26 |
10,778 |
1,078 |
12,989 |
1,299 |
28 |
10,643 |
1,064 |
13,030 |
1,303 |
30 |
10,532 |
1,053 |
13,102 |
1,310 |
32 |
10,489 |
1,049 |
13,170 |
1,317 |
34 |
10,533 |
1,053 |
13,255 |
1,326 |
36 |
10,689 |
1,069 |
13,346 |
1,335 |
38 |
11,005 |
1,105 |
13,440 |
1,344 |
40 |
11,596 |
1,160 |
13,548 |
1,355 |
42 |
12,480 |
1,248 |
13,653 |
1,365 |
Wykres 1. Zależność okresu T [s] od położenia ciężarka x [cm] dla ostrza A i ostrza B.
Punktem przecięcia krzywych przyjęliśmy ![]()
[cm]. Ponieważ w zakres ćwiczenia nie wchodziło precyzyjne wyznaczenie okresu w warunkach odwracalności (pomiar 100 okresów), okres wahań obliczyliśmy jako średnią arytmetyczną okresów wahań dla położeń ![]()
.
![]()
Odległość między ostrzami wynosiła ![]()
Obliczyliśmy wartość przyśpieszenia ziemskiego ze wzoru ( 5 ):
![]()
Dyskusja błędów.
Dokładność przyrządu mierzącego okres wynosiła ![]()
(wg skryptu). My niepewność ![]()
obliczyliśmy z odchylenia standardowego średniej dla małej ilości pomiarów ![]()
.
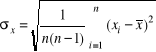
( 6 )
W naszym przypadku liczyliśmy średnią z ![]()
pomiarów. Niepewność pomiaru ![]()
wynosi:
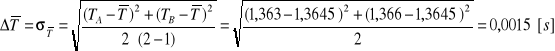
Ostatecznie:
![]()
.
Pomiaru odległości między ostrzami dokonano za pomocą taśmy mierniczej. Za niepewność pomiaru odległości przyjęliśmy ![]()
.
![]()
![]()
Błąd obliczenia stałej grawitacji obliczyliśmy przy pomocy propagacji niepewności złożonej wg wzoru:
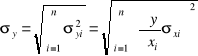
( 7 )

W wyniku przeprowadzonych pomiarów oraz obliczeń wyznaczyliśmy wartość stałej grawitacji:
![]()
.
Wnioski.
Otrzymana przez nas wartość przyśpieszenia ziemskiego niewiele różni się od wartości tablicowej
(w granicy 1%), która wynosi:
![]()
Ćwiczenie wykazało, że nawet w prostym ćwiczeniu laboratoryjnym można wyznaczyć stałą grawitacji z nienajgorszym przybliżeniem.
Na dokładność wyznaczenia przyśpieszenia ziemskiego wykonanego przez nas bardzo miały między innymi następujące czynniki:
precyzyjne wprawienie w ruch wahadła (kąt, płaszczyzna)
dokładne wyznaczenie położenia ruchomego ciężarka (położenie było zmieniane co 2 [cm])
opory powietrza
Mimo tego doświadczenie wykazało, że dla małych wychyleń kątowych okres drgań wahadła nie zależy od jego amplitudy.
Wartość ta, ustalona przez Międzynarodowy Komitet Miar i Wag w roku 1901, odnosi się do szerokości geograficznej ![]()
na poziomie morza (R. Resnick, D. Halliday „Fizyka 1”, wyd. PWN, Warszawa 2001)
1
Wyszukiwarka
Podobne podstrony:
cw26(teoria), Studia PWr W-10 MBM, Semestr II, Fizyka, Fizyka - laborki, Fizyka - laborki, Fizyka La
cw31(teoria), Studia PWr W-10 MBM, Semestr II, Fizyka, Fizyka - laborki, Fizyka - laborki, Fizyka La
cw21(teoria), Studia PWr W-10 MBM, Semestr II, Fizyka, Fizyka - laborki, Fizyka - laborki, Fizyka La
modu- younga, Studia PWr W-10 MBM, Semestr II, Fizyka, Fizyka - laborki, Fizyka - laborki, Fizyka La
cw31 - wykres (aproksymacja prosta), Studia PWr W-10 MBM, Semestr II, Fizyka, Fizyka - laborki, Fizy
fala dzwiekowa, Studia PWr W-10 MBM, Semestr II, Fizyka, Fizyka - laborki, Fizyka - laborki, Fizyka
cw43(teoria), Studia PWr W-10 MBM, Semestr II, Fizyka, Fizyka - laborki, Fizyka - laborki, Fizyka La
teory cw.2b, Studia PWr W-10 MBM, Semestr II, Fizyka, Fizyka - laborki, Fizyka - laborki, Fizyka Lab
cw44(wykresy), Studia PWr W-10 MBM, Semestr II, Fizyka, Fizyka - laborki, Fizyka - laborki, Fizyka L
Ăwiczenie 15-16, Studia PWr W-10 MBM, Semestr II, Fizyka, Fizyka - laborki, Fizyka - laborki, Fizyka
cw22(wykresy), Studia PWr W-10 MBM, Semestr II, Fizyka, Fizyka - laborki, Fizyka - laborki, Fizyka L
cw44(teoria), Studia PWr W-10 MBM, Semestr II, Fizyka, Fizyka - laborki, Fizyka - laborki, Fizyka La
cw31 - wykres (aproksymacja wielomianem), Studia PWr W-10 MBM, Semestr II, Fizyka, Fizyka - laborki,
cw22(teoria), Studia PWr W-10 MBM, Semestr II, Fizyka, Fizyka - laborki, Fizyka - laborki, Fizyka La
cw43(wykresy), Studia PWr W-10 MBM, Semestr II, Fizyka, Fizyka - laborki, Fizyka - laborki, Fizyka L
opracowanie wynikow pomiarow, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laborator
cw26 (teoria++), Studia PWr W-10 MBM, Semestr II, Fizyka, Fizyka - laborki, Fizyka - laborki, Fizyka
LABORKA2, Biotechnologia, Fizyka, Labolatorium
więcej podobnych podstron