Opracowanie wyników pomiarów

Przeprowadzono serię 71 pomiarów zależności transmisji od długości fali, wykorzystując w tym celu spektrometr SPECOL. Pomiar przeprowadzono dla długości fal z zakresu (380-758)nm.

Dane doświadczalne zawarto w tabeli 1. Następnie sporządzono wykres transmisji do długości fali (wykres 1). Na wykresie tym zaznaczono obszar silnej i słabej absorpcji. Jako granice obszarów przyjęto 485nm, czyli punkt pomiarowy, w którym dochodzi do zmiany przebiegu krzywej wykresu, w stosunku do jej wcześniejszego biegu (jako przybliżenie przecięcia się obwiedni oscylacji).

Posługując się wzorem
, obliczono energie fotonów dla poszczególnych długości fali, dzięki czemu możliwe było sporządzenie wykresu zależności transmisji od energii fotonu (wykres 2). Jak łatwo zaobserwować, jest to zależność odwrotnie proporcjonalna.

Błędy pomiarowe uwzględnione w tabeli 1 wypływają w prostej linii z niedokładności przyrządu pomiarowego, a w przypadku energii fotonu, zostały wyliczone z prawa przenoszenia niepewności pomiarowej.

λ[nm]		T[%]		E[eV]			α(E)	λ[nm]		T[%]		E[eV]
380	±1	2	±1	3,262105	±	0,000009	5,101	590	±1	83	±1	2,101017	±	0,000004
390				3			3,178462			0,000008		4,555		595		83		2,083361		0,000004
400				5			3,099000			0,000008		3,868		600		85		2,066000		0,000003
410				10			3,023415			0,000007		2,934		605		84		2,048926		0,000003
420				16			2,951429			0,000007		2,302		610		86		2,032131		0,000003
430				24			2,882791			0,000007		1,756		615		87		2,015610		0,000003
440				32			2,817273			0,000006		1,368		620		89		1,999355		0,000003
450				41			2,754667			0,000006		1,035		625		91		1,983360		0,000003
460				50			2,694783			0,000006		0,767		630		92		1,967619		0,000003
470				58			2,637447			0,000006		0,568		635		95		1,952126		0,000003
480				64			2,582500			0,000005		0,435		640		97		1,936875		0,000003
485				65			2,555876			0,000005		0,414		645		98		1,921860		0,000003
490				66			2,529796			0,000005				650		98		1,907077		0,000003
495				67			2,504242			0,000005					655		100		1,892519		0,000003
500				68			2,479200			0,000005					660		99		1,878182		0,000003
505				70			2,454653			0,000005					665		98		1,864060		0,000003
510				73			2,430588			0,000005					670		100		1,850149		0,000003
515				77			2,406990			0,000005					675		100		1,836444		0,000003
520				79			2,383846			0,000005					680		98		1,822941		0,000003
525				83			2,361143			0,000004					685		97		1,809635		0,000003
530				85			2,338868			0,000004					690		96		1,796522		0,000003
535				91			2,317009			0,000004					695		94		1,783597		0,000003
537				89			2,308380			0,000004					700		95		1,770857		0,000003
540				90			2,295556			0,000004					705		92		1,758298		0,000002
542				91			2,287085			0,000004					710		91		1,745915		0,000002
545				92			2,274495			0,000004					715		90		1,733706		0,000002
547				93			2,266179			0,000004					720		91		1,721667		0,000002
550				92			2,253818			0,000004					725		88		1,709793		0,000002
555				91			2,233514			0,000004					730		88		1,698082		0,000002
560				90			2,213571			0,000004					735		88		1,686531		0,000002
565				88			2,193982			0,000004					740		85		1,675135		0,000002
570				86			2,174737			0,000004					745		86		1,663893		0,000002
575				85			2,155826			0,000004					750		85		1,652800		0,000002
580				84			2,137241			0,000004					755		85		1,641854		0,000002
585				83			2,118974			0,000004					758		86		1,635356		0,000002
587				83			2,111755			0,000004

Tabela 1

Wykres 1

Wykres 2

W obszarze słabej absorpcji zauważalne są charakterystyczne oscylacje, wynikające z wielokrotnego wewnętrznego odbicia fali wewnątrz badanej próbki. Minima i maksima interferencyjne, jak również obwiednie współczynnika transmisji T_min i T_max­ zawarto w tabeli 2.

		T[%]	λ[nm]
Maksima i minima interferencyjne	T_max	93	547
		T_min	83	595
		T_max 2	100	675
		T_min 2	85	755
Obwiednia	T_max	100
		T_min	85

Tabela 2

Wykorzystując dane zawarte w tabeli 2 oraz wzór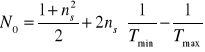
, obliczono wartość N₀: N₀=(2,19±0,07).

Otrzymana wartość N₀ posłużyła następnie do wyznaczenia współczynnika załamania cienkiej warstwy (przyjęto n_s=1,52): n=(1,94±0,09).

Opierając się na wyznaczonym współczynniku cienkiej warstwy, danych zawartych w tabeli 2 oraz na wzorze
, gdzie λ₁, λ₂ - długości fali odpowiadające dwóm kolejnym maksimom lub minimom interferencyjnym, obliczono grubość badanej warstwy, dla dwóch kolejnych maksimów i minimów. Dla wyznaczonych wielkości wyznaczono błędy pomiarowe metodą różniczki zupełnej. Celem ostatecznego wyliczenia grubości warstwy, obliczono średnią arytmetyczną otrzymanych wcześniej wartości. Podobnie postąpiono w stosunku do niepewności pomiarowych (co wynika z prawa przenoszenia błędu). Ostatecznie obliczono: d=(0,73±0,04)μm.

Wykorzystując przybliżenie, dla obszaru silnej absorpcji:
, gdzie: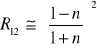
oraz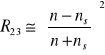
, a także z pewnym przybliżeniem przenosząc współczynnik załamania n cienkiej warstwy do obszaru silnej absorpcji, wyznaczono zależność współczynnika absorpcji do energii fotonu: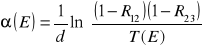
. Wartości współczynnika absorpcji zawarto w tabeli 1. Oczywistym jest fakt, że wyznaczono wartości α tylko dla obszaru o silnej absorpcji. Zależność współczynnika absorpcji od energii fotonu przedstawia wykres 3.

Wykres 3

Na koniec przystąpiono do obliczenia przerwy energetycznej. Obliczając E_g posłużono się wzorem:
, który po pewnych przekształceniach, daje się przedstawić w postaci:
. Dzięki tej transformacji w łatwy sposób można obliczyć przerwę energetyczną w półprzewodniku. Cały problem ogranicza się do aproksymacji wykresu powyższej zależności i wyznaczenia punktu przecięcia się trendu z osią energii.

Wykonując odpowiednie obliczenia, sporządzono cztery wykresy wspomnianej zależności, dla czterech różnych wartości parametru m. Dla m=1/2 odrzucono punkty pomiarowe, które znacznie odbiegały od wykreślonego trendu, traktując je jako błędy grube.

Wartości E_g dla poszczególnych m:

m=1/2	Eg =	2,9 eV	dla przejść prostych dozwolonych
m=3/2			2,5 eV	dla przejść prostych wzbronionych
m=2			2,3 eV	dla przejść skośnych dozwolonych
m=3			2,1 eV	dla przejść skośnych wzbronionych

Spośród obliczonych potencjalnych wartości E_g wybrano wartość odpowiadającą m=1/2 (przejście proste dozwolone). Głównym powodem takiego wyboru był fakt, ze tylko w tym przypadku, wartość E_g leżała w obszarze silnej absorpcji. Pozostałe wartości przerwy energetycznej odrzucono, mimo, iż w tych przypadkach, znacznie więcej punktów leżało na odcinkach prostoliniowych.

Ostatecznie, dla m=1/2:

Równanie prostej aproksymacyjnej wyraża się wzorem: y = (628,6±44,6)x - (1807,7±136,9)

E_g = (2,9±0,4)eV

Błąd pomiarowy wyznaczono, korzystając z prawa przenoszenia niepewności pomiarowej.

Błąd względny wyznaczonej przerwy energetycznej wyniósł: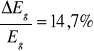
.

Wnioski:

Pierwsza uwaga jaka się narzuca, to duży błąd towarzyszący wyznaczeniu E_g, rzędu 14,7%. Błąd ten wynika z niedoskonałości przyrządu pomiarowego, nieścisłego (na oko) skalowania przyrządu pomiarowego przed każdym pomiarem, jak również, złożoności obliczeń, jakie należało wykonać, alby otrzymać ostateczny wynik. Te wszystkie czynniki złożyły się na tak duży błąd pomiarowy przy wyznaczaniu E_g.

Należy również zwrócić szczególną uwagę na trudności związane z weryfikacją ostatecznie otrzymanych potencjalnych wartości E_g. Niestety, nie możliwe było jednoznaczne określenie, z jakiego typu przerwą mamy do czynienia, dokonana selekcja nie jest bowiem stuprocentowo pewna.

---