Opracowanie wyników

Pomiary z doświadczenia:

λ[nm]	Współczynnik transmisji T[%]	λ[nm]	Współczynnik transmisji T[%]
380	0	525	81
385	3	530	84
390	3	535	88
395	5	540	90
400	7	545	92
405	9	550	93
410	11	555	92
415	13	560	91
420	16	565	90
425	20	570	89
430	24	580	85
435	27	590	84
440	31	600	85
445	35	610	86
450	40	620	88
455	45	630	91
460	49	640	94
465	54	650	98
470	58	660	99
475	61	670	98
480	63	680	98
485	65	690	97
490	67	700	96
495	67	710	93
500	69	720	92
505	69	730	90
510	72	740	87
515	74	750	86
520	77	760	87

1. Sporządzić wykres eksperymentalnej zależności współczynnika transmisji T w funkcji długości fali λ dla badanej cienkiej warstwy. Przeliczyć długości fali λ wyrażoną w µm na energię fotonu E w elektronowoltach eV.

Wykres eksperymentalnej zależności współczynnika transmisji T od długości fali λ

Energia jest wyliczana z zależności:

Wykres zależności współczynnika transmisji T od energii foronu

Można przyjąć ze obszar silnej absorpcji zaczyna się od 2.4 eV. Wraz ze wzrostem energii rośnie absorpcja.

2. W obszarze słabej absorpcji (II), gdy grubość cienkiej warstwy d jest porównywalna z długością fali λ, w wyniku interferencji pojawiają się charakterystyczne oscylacje współczynnika transmisji T. W obszarze tym należy graficznie wyznaczyć obwiednie współczynnika transmisji Tmax i Tmin.

Na podstawie doświadczalnych wyników w obszarze słabej absorpcji

Wyliczamy
a następnie współczynnik załamania n cienkiej warstwy według wzorów:

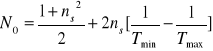
gdzie

Po podstawieniu wartości liczbowych:

3. W obszarze słabej absorpcji II można również wyznaczyć grubość warstwy d i porównać otrzymaną wartość z grubością zmierzoną innymi metodami (np. za pomocą profilometru).

po wyznaczeniu długości fali λ1 i λ2 odpowiadających dwóm kolejnym maksimom lub minimom interferencyjnym współczynnika transmisji T.

, gdzie
to długość fali odpowiadających dwóm kolejnym maksimom lub minimom interferencyjnym współczynnika transmisji T.

 

Po podstawieniu wartości liczbowych
d=846,15 nm

4.Mozna obliczyć w obszarze silnej absorpcji R₁₂ i R₂₃, korzystając z zależności:

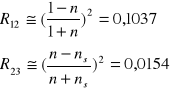
Obliczenie i sporządzenie wykresu zależności współczynnika absorpcji α w funkcji energii fotonu E:

Dla małych energii wykres przyjmuje ujemne wartości, zaś dla wysokich energii wykres jest poprawny. Świadczy to o tym ze wzór jest poprawny tylko dla wyższych energii

5. Wyznaczyć wartość przerwy energetycznej Eg ze wzoru:

gdzie m przyjmuje jedną z wartości: m=1/2 dla przejść prostych dozwolonych, m=3/2 dla przejść prostych wzbronionych, m=2 dla przejść skośnych dozwolonych, m=3 dla przejść skośnych wzbronionych a Cm jest stałą zależną od rodzaju przejścia optycznego. Aby wyznaczyć wartość Eg najwygodniej jest wykreślić zależność
d la każdej możliwej wartości m i z dopasowania prostej do danych eksperymentalnych odczytać punkt przecięcia prostej z osią energii.

Aby wyznaczyć punkt przecięcia prostej z osią energii korzystamy z metody regresji liniowej:

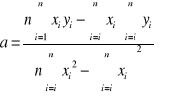
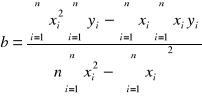
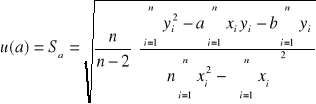
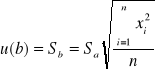
Następnie obliczamy bład wyznaczania przerwy energetycznej metodą różniczki zupełnej:

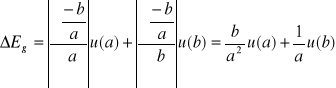
Dla m=0,5

a=392,558

b=-1114,654

u(a)= 2,089

u(b)= 6,294

Eg=2,84

∆Eg=0,311

Dla 1.5

a=7,421

b=--18,522

Eg=2,49

u(a)=0,182

u(b)=0,559

∆Eg=0,014

m=2

a=9,768

b= -25,523

Eg=2,61

u(a)= 0,022

u(b)= 0,063

∆Eg=0,001

m=3

a=7,421

b=-18,522

Eg=2,50

u(a)= 0,182

u(b)=0,529

∆Eg=0,408

6. Analizując kolejne z powyższych wykresów wybieramy energię
czyli przejście proste dozwolone. Chociaż na pozostałych wykresach punkty leżą blisko prostej regresji ale energie te leża w obszarze słabej absorpcji.

7. . Błąd pomiaru energii
wynika z niedokładności śruby regulującej długość fali oraz z maksymalnego błędu odczytu współczynnik transmisji. Korzystając z wcześniejszych obliczeń:

Eg=2,61

u(a)= 0,022

u(b)= 0,063

∆Eg=0,001

---