Opracowanie wyników
Opór obciążenia liczymy bezpośrednio z prawa Ohma wykorzystując wzór R=U/I.
Moc obliczamy z wzoru Pu=UI.
Lp. |
U [V] |
Ir [mA] |
R [W] |
DR |
Pu [mW] |
P [mW] |
h |
R/r |
1 |
2,64 |
1,26 |
2095,24 |
15,14 |
3,33 |
3,68 |
0,90 |
0,11 |
2 |
2,63 |
1,29 |
2038,76 |
14,77 |
3,39 |
3,77 |
0,90 |
0,11 |
3 |
2,63 |
1,31 |
2007,63 |
14,54 |
3,45 |
3,83 |
0,90 |
0,11 |
4 |
2,62 |
1,35 |
1940,74 |
14,09 |
3,54 |
3,94 |
0,90 |
0,12 |
5 |
2,61 |
1,38 |
1891,30 |
13,77 |
3,60 |
4,03 |
0,89 |
0,12 |
6 |
2,60 |
1,41 |
1843,97 |
13,46 |
3,67 |
4,12 |
0,89 |
0,12 |
7 |
2,60 |
1,45 |
1793,10 |
13,09 |
3,77 |
4,23 |
0,89 |
0,12 |
8 |
2,59 |
1,48 |
1750,00 |
12,80 |
3,83 |
4,32 |
0,89 |
0,13 |
9 |
2,58 |
1,52 |
1697,37 |
12,45 |
3,92 |
4,44 |
0,88 |
0,13 |
10 |
2,57 |
1,56 |
1647,44 |
12,11 |
4,01 |
4,56 |
0,88 |
0,14 |
11 |
2,56 |
1,60 |
1600,00 |
11,79 |
4,10 |
4,67 |
0,88 |
0,14 |
12 |
2,55 |
1,65 |
1545,45 |
11,42 |
4,21 |
4,82 |
0,87 |
0,14 |
13 |
2,54 |
1,69 |
1502,96 |
11,13 |
4,29 |
4,93 |
0,87 |
0,15 |
14 |
2,53 |
1,75 |
1445,71 |
10,74 |
4,43 |
5,11 |
0,87 |
0,15 |
15 |
2,52 |
1,80 |
1400,00 |
10,42 |
4,54 |
5,26 |
0,86 |
0,16 |
16 |
2,50 |
1,86 |
1344,09 |
10,06 |
4,65 |
5,43 |
0,86 |
0,17 |
17 |
2,49 |
1,92 |
1296,88 |
9,73 |
4,78 |
5,61 |
0,85 |
0,17 |
18 |
2,47 |
1,99 |
1241,21 |
9,36 |
4,92 |
5,81 |
0,85 |
0,18 |
19 |
2,46 |
2,07 |
1188,41 |
8,99 |
5,09 |
6,04 |
0,84 |
0,19 |
20 |
2,44 |
2,15 |
1134,88 |
8,63 |
5,25 |
6,28 |
0,84 |
0,20 |
21 |
2,42 |
2,23 |
1085,20 |
8,29 |
5,40 |
6,51 |
0,83 |
0,21 |
22 |
2,40 |
2,32 |
1034,48 |
7,95 |
5,57 |
6,77 |
0,82 |
0,22 |
23 |
2,38 |
2,43 |
979,42 |
7,57 |
5,78 |
7,10 |
0,82 |
0,23 |
24 |
2,36 |
2,52 |
936,51 |
7,27 |
5,95 |
7,36 |
0,81 |
0,24 |
25 |
2,33 |
2,65 |
879,25 |
6,89 |
6,17 |
7,74 |
0,80 |
0,25 |
26 |
2,30 |
2,77 |
830,32 |
6,56 |
6,37 |
8,09 |
0,79 |
0,27 |
27 |
2,26 |
2,93 |
771,33 |
6,16 |
6,62 |
8,56 |
0,77 |
0,29 |
28 |
2,23 |
3,09 |
721,68 |
5,82 |
6,89 |
9,02 |
0,76 |
0,31 |
29 |
2,19 |
3,28 |
667,68 |
5,45 |
7,18 |
9,58 |
0,75 |
0,34 |
30 |
2,14 |
3,49 |
613,18 |
5,08 |
7,47 |
10,19 |
0,73 |
0,37 |
31 |
2,08 |
3,73 |
557,64 |
4,71 |
7,76 |
10,89 |
0,71 |
0,40 |
32 |
2,02 |
4,01 |
503,74 |
4,33 |
8,10 |
11,71 |
0,69 |
0,44 |
33 |
1,96 |
4,31 |
454,76 |
3,99 |
8,45 |
12,59 |
0,67 |
0,49 |
34 |
1,86 |
4,75 |
391,58 |
3,56 |
8,84 |
13,87 |
0,64 |
0,57 |
35 |
1,77 |
5,15 |
343,69 |
3,23 |
9,12 |
15,04 |
0,61 |
0,65 |
36 |
1,64 |
5,71 |
287,22 |
2,85 |
9,36 |
16,67 |
0,56 |
0,78 |
37 |
1,50 |
6,35 |
236,22 |
2,49 |
9,53 |
18,54 |
0,51 |
0,95 |
38 |
1,28 |
7,32 |
174,86 |
2,06 |
9,37 |
21,37 |
0,44 |
1,28 |
39 |
1,04 |
8,40 |
123,81 |
1,70 |
8,74 |
24,53 |
0,36 |
1,81 |
40 |
0,66 |
10,09 |
65,41 |
1,28 |
6,66 |
29,46 |
0,23 |
3,42 |
41 |
0,14 |
12,41 |
11,28 |
0,86 |
1,74 |
36,24 |
0,05 |
19,86 |
Σ |
90,09 |
0,13 |
|
|
0,23 |
|
|
|
|
|
|
|
|
|
|
|
|
ΔU |
0,01 |
V |
|
S(r) [Ω] |
0,17 |
|
Σ X^2 |
= 0,00068 |
ΔI |
0,01 |
mA |
|
S(ε) [V] |
0,0007 |
|
Σ y^2 |
= 210,77 |
r |
223,97 |
Ω |
|
S(r)/r [%] |
0,08 |
|
|
|
ε |
2,92 |
V |
|
S(ε)/ε [%] |
0,02 |
|
|
|
Wykres zależności U=f(I) wraz z aproksymacją.
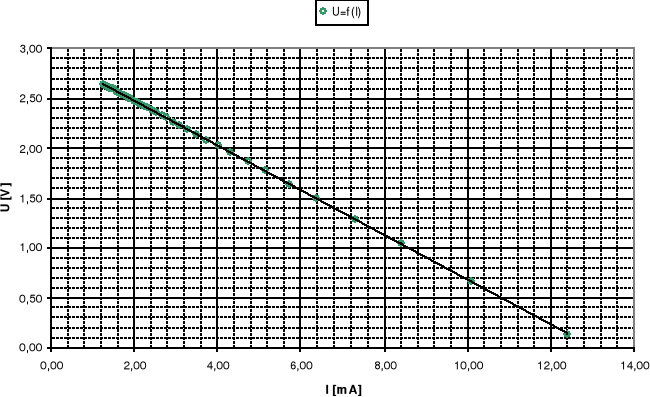
Wykres zależności U(I) jest liniowy. Można opisać go równaniem f(I) = a - bI, gdzie w naszym przypadku f(I) - U, a = ε, b = r. Do wyznaczenia a i b posłużyłem się metoda regresji liniowej (obliczone wartości znajdują się w tabelce pkt1).
Do wyznaczenia błędu pomiaru Δε i Δr skorzystam z metody najmniejszych kwadratów.
![]()
![]()
W tym celu należy policzyć
(gdzie a=-0, 223,97 b=2,92)
Błąd Δε wynosi
![]()
![]()
natomiast Δr
Moc całkowitą obliczam z wzoru P=εI
natomiast sprawność η z zależności η=Pu/P
Wyniki umieszczone zostały umieszczone w tabelce.
6. Wykresy mocy użytecznej, mocy całkowitej oraz sprawności w funkcji stosunku oporności obciążenia do oporności wewnętrznej R/r
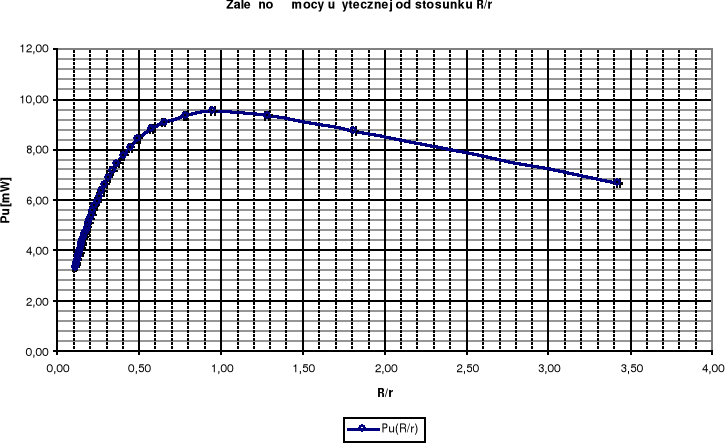
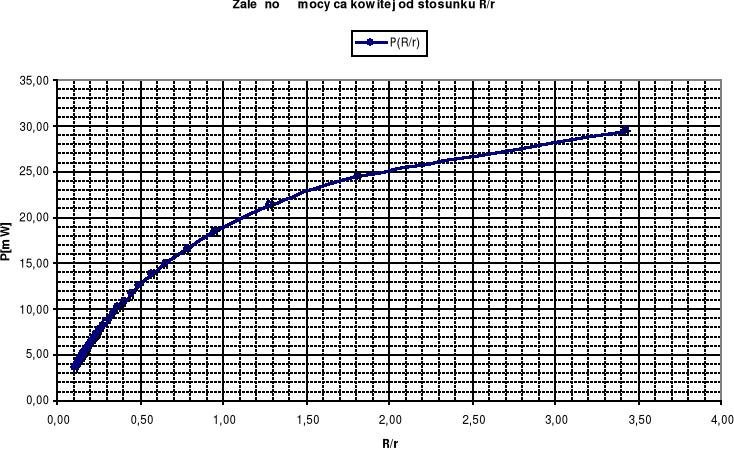
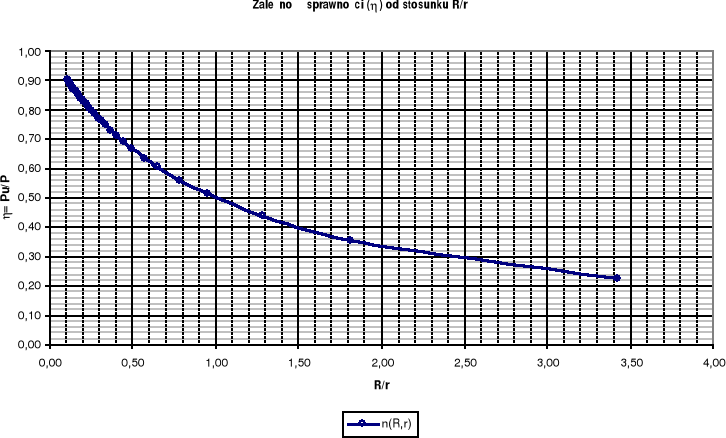
Z wykresu zależności Pu(R/r) wynika, że moc użyteczna osiąga wartość maksymalną dla oporu zewnętrznego bliskiego oporowi wewnętrznemu źródła zasilania (R/r = 0,95) Dla powyższej wartości oporu odbiornika sprawność η=0,51. Można się domyślić, że Pu osiągnie wartość maksymalna dla R/r = 1, a sprawność dla tak zestawionego układu będzie równa 0,5.
Z ćwiczenia wynika, że największą moc użyteczną można otrzymać dla odbiornika o oporze wewnętrznym równym oporowi wewnętrznemu źródła zasilania.
Ponadto można zauważyć, że największa sprawność jest osiągana dla małych prądów i spada ona wraz ze wzrostem prądu.
Duży spadek sprawności przy większym natężeniu wynika ze strat energii na oporze wewnętrznym źródła zasilania. Aby unikać takich strat należy budować źródła zasilania o oporze wewnętrznym dopasowanym do docelowego odbiornika złe dopasowanie wiąże się z tym niebezpieczeństwo, że podczas zwarcia w obwodzie popłynie bardzo duży prąd, bądź źródło zostanie bardzo szybko rozładowane.
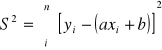
![]()
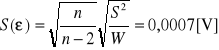
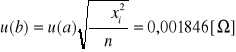
Wyszukiwarka
Podobne podstrony:
konspekt Cw5, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, 5,4 Badanie
Dok1, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, 5,4 Badanie zależno
[3]opracowanie v1.0, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, labo
Opracowanie wyników 6, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, la
Opracowanie wyników, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, 12 W
opracowanie wyników, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, labo
Opracowanie 051, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
[3]opracowanie v1.0, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, labo
[4]opracowanie, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
[7]opracowanie, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
opracowanie cw 9, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki
Opracowanie Cw 7, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki
8 opracowanie, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, l
[10]opracowanie, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
[8]opracowanie, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
cw 11- opracowanie, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, labor
Opracowanie Cw4 moje, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, lab
[3]opracowaniemoje, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, labor
10 opracowanie, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
więcej podobnych podstron