Spis treści

Praca domowa nr 2 obejmowała cztery zadania:

Zadanie nr 1.

Wyprowadzić równanie dynamiki płynu lepkiego, rozważania opatrzyć komentarzami i stosownymi ilustracjami.

Zadanie nr 2.

Rozważamy gaźnik elementarny którego konstrukcję charakteryzujemy trzema wymiarami:

d - średnica dyszy;

D - średnica gardzieli;

h - wysokość poziomu paliwa w komorze pływakowej;

natomiast rozpatrywane warunki pracy silnika określają następujące wskaźniki:

N - moc [kW];

g_e - jednostkowe zużycie paliwa [g/kWh];

ρ_p - gęstość powietrza 1.3kg/m³ ;

ρ_b - gęstość benzyny 700kg/m³ ;

λ - współczynnik nadmiaru powietrza (bezwymiarowy);

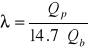
gdzie:

Q_p - wydatek powietrza zasysanego przez silnik [kg/s];

Q_b - wydatek paliwa spalanego w silniku [kg/s].

Należy wyznaczyć wartość jednego wskazanego wymiaru,

natomiast wartości pozostałych pięciu odczytać z tabeli danych

zadania.

Zadanie 3

Wyznaczyć nominalny wydatek wody napływającej na łopatki

wirnika turbiny Peltona oraz

- obliczyć nominalną średnicę dyszy wypływowej (d₀);

- obliczyć siłę naporu wody na łopatki turbiny.

Dane:

H - wysokość spadu wody [m];

N - nominalna moc turbiny [kW];

α- nominalna wartość współczynnika prędkości turbiny;

β - kąt rozwarcia łopatek turbiny [°];

r - promień turbiny [m];

u - obwodowa prędkość łopatek turbiny [m/s];

v₀ - prędkość wody wypływającej z dyszy [m/s].

Zadanie 4

Wyznaczyć moc pompy wyporowej tłoczącej wodę do zbiorników wieżowych. Sprawdzić czy w instalacji nie powstaje kawitacja. Schemat instalacji według rysunku.

Parametry instalacji hydraulicznej:

Q - wydatek pompowania [dm³ /s];

d - średnica rurociągu [mm];

h₁, h₂, h₃, h₄ - wysokości pompowania [m];

l₁, l₂, l₃, l₄, l₅ - długości rurociągu [m];

ζ_f, ζ_k, ζ_z, ζ_t- współczynniki strat lokalnych;

p_min- ciśnienie zabezpieczające przed parowaniem wody w warunkach normalnych;

p_min = 15 kPa

ρ - gęstość wody 1000 kg/m³ ;

ν - lepkość kinematyczna wody 1.0∙10^-6 m²/s;

Zależności istniejące w rurociągu:

l₄ = 5l₂;

l₅= l₃;

h₄= h₃;

ζ_t= 2ζ_k

Dane do zadań zawarte są w załączonym pasku

Grupa: 2.6		Zadanie 2						Zadanie 3					Zadnie 4
L.p.	Nr Alb	d [mm]	D [mm]	h [mm]	N [kW]	ge [g/kWh]	λ	N [kW]	H [m]	r [m]	α	β [°]	Q [l/s]	d [mm]	h1 [m]	h2 [m]	h3 [m]	L1 m]	L2 [m]	L3 [m]	ζf	ζk	ζz
27	222319	?	23	8	17	270	1,05	130	110	0,6	0,44	16	57	260	1,7	6,5	22	31	110	210	5	0,25	0,55

Zadanie 1.

Wyprowadzić równanie dynamiki płynu lepkiego, rozważania opatrzyć komentarzami i

Ilustracjami,

1. Wstęp

Płyn rzeczywisty charakteryzuje się lepkością (tarciem wewnętrznym), która ujawnia się w czasie ruchu. Podczas ruchu płynu lepkiego na każdą jego cząstkę i na każdy element jego masy działają w ogólnym przypadku siły masowe (objętościowe) i powierzchniowe mające składowe normalne i styczne. Składowe styczne (ścinające) są wywołane lepkością cieczy.

Lepkość jest to zdolność płynów do przenoszenia naprężeń stycznych przy wzajemnym przemieszczaniu elementów poruszających się z różnymi prędkościami.

Założeniem podstawowym pozwalającym związać ilościowo stan naprężeń powierzchniowych z polem prędkości jest hipoteza Newtona. Zgodnie z tą hipotezą naprężenie styczne jest proporcjonalne do gradientu prędkości.

.

gdzie: μ - współczynnik lepkości dynamicznej (lepkość dynamiczna),[Pa·s].

Płyny spełniające powyższą relację są nazywane niutonowskimi.

Zakłada się ponadto, że naprężenia styczne w poruszającym się płynie lepkim są proporcjonalne do prędkości odkształceń postaciowych (kątowych) elementu płynu., czyli, że

Tensorowe sformułowanie hipotezy Newtona ma postać

, (1)

w którym S_D - tensor prędkości odkształcenia postaciowego (dewiator).

Tensor naprężeń б będzie miał wówczas postać:

, (2)

gdzie: -p∙I - tensor kulisty (aksiator) opisujący matematycznie naprężenia normalne

wszechstronnego ściskania występujące w płynie doskonałym(płynie

Pascala)

б_L - tensor naprężeń (dewiator) opisujący odkształcenia postaciowe

wynikające z lepkości płynu ( zgodnie z hipotezą Newtona)

2. Wyprowadzenie równania dynamiki płynu lepkiego.

Przy wyprowadzeniu równania korzystałem z uogólnionej postaci drugiej zasady dynamiki Newtona (z zasady ilości ruchu): „pochodna pędu ( zmiana pędu w czasie) dla każdego obszaru Ω jest równa sumie sił działających na ten obszar ^,, , czyli:

. (3)

Kształt równania (3) ukierunkował tryb wyprowadzenia równania równowagi w dwóch krokach:

-w pierwszym kroku określę siłę F_Ω(t),

-w drugim - pochodną pędu
.

W konsekwencji zgodnie z równaniem (3) obie wielkości porównam.

1. Określenie siły F_Ω(t) działającej na obszar Ω ( oznaczenia zgodne z rys. 1.).

Rys. 1

(4)

Po zastosowaniu twierdzenia Gaussa - Ostrogradskiego

. (5)

Sumując wyrażenia podcałkowe otrzymałem:

. (6)

Dla płynu lepkiego- niutonowskiego naprężenie w danym punkcie cieczy opisuje równanie ( 2 )

, natomiast
(równanie (1) ).

( S_D - dewiator prędkości odkształcenia postaciowego )

Po podstawieniu :

, (7)

dywerygencja pod całką w równaniu (6) przyjmie postać:

(8)

Zastępując div σ pod całką z równania (6) wyrażeniem (8) otrzymałem:

(9)

gdzie:
V - operator Laplace'a(definicja na stronie 6) zastosowany dla wektora pola prędkości V:

.

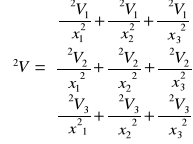
2. Określnie pochodnej pędu dla obszaru Ω (oznaczenia zgodne z rys. 2. ) .

Rys.2

Na podstawie bilansu pędu jego pochodna

, (10)

a po zastosowaniu twierdzenia Gaussa - Ostrogradskiego

. (11)

Ponieważ P = ρ∙V oraz J_P = V ∙ P^T , wówczas wyrażenie div J_P pod całką

przyjmie postać

. (12)

Podstawiając zależność (12) do równania (11) otrzymamy:

. (13)

Ale
jest pochodną substancjalną i po wprowadzeniu jej do równania (13)

(14)

Uwzględniając, że P = ρ∙V, i
to po podstawieniu do wzoru (14):

, (15)

Biorąc pod uwagę prawo zachowania masy (

) ,

równanie (15) zredukuje się do zależności:

. (16)

3. Ustalenie równania równowagi

Porównując zależności (9) i (16) zgodnie z warunkiem (3) otrzymałem:

,

Co oznacza, że funkcje podcałkowe muszą być tożsamościowo równe tzn.

. (17)

Równanie (17) wraz z równaniami:

- prawo zachowania masy (ciągłości)

ρ = φ (p) , - gęstość płynu w funkcji ciśnienia,

stanowi najogólniejszą formę równań dynamiki płynu lepkiego ściśliwego, przy stałej wartości współczynnika lepkości μ, które są znane pod nazwą równań Naviera - Stokesa.

______________________

Uzupełnienie:

Na podstawie literatury: W.Krysicki, L.Włodarski: Analiza Matematyczna w Zadaniach. PWN ,Warszawa 2008

Laplasjan (operator Laplace'a) - operator różniczkowy oznaczany
(lub ∆) przyporządkowuje dwukrotnie różniczkowalnej funkcji F(x,y,z) jej sumę drugich pochodnych cząstkowych po kartezjańskich współrzędnych przestrzennych:

.Zadanie 2

Wyznaczyć średnicę dyszy d gaźnika elementarnego o ustalonych danych konstrukcyjnych i warunkach pracy silnika ( wg tabeli danych ).

1. Dane i założenia

d = ? mm - średnica dyszy gaźnika-podlega

wyznaczeniu

D = 23 mm = 0,023 m - średnica gardzieli,

h = 8 mm = 0,008 m - wysokość poziomu paliwa w komorze,

pływakowej,

N = 17 kW - moc silnika,

g_e = 270 g/kWh - jednostkowe zużycie paliwa,

ρ_p = 1,3 kg/m - gęstość powietrza,

ρ_b = 700 kg/m - gęstość paliwa (benzyna),

λ =
- współczynnik nadmiaru powietrza

( bezwymiarowy ),

gdzie:

Q_p kg/s - wydatek masowy powietrza zassanego przez silnik ,

Q_b kg/s - wydatek masowy paliwa spalanego w silniku .

Uwaga: w przyjętych oznaczeniach dolne indeksy: b - dotyczą benzyny,

p - powietrza, natomiast cyfry: 0,1,2, oznaczają rozpatrywane przekroje.

Rys.1.

Schemat gaźnika wraz z oznaczeniami i rozpatrywanymi przekrojami przedstawiłem na rys.1.

2. Obliczenia

1. Obliczam wydatek masowy paliwa jako iloczyn jednostkowego zużycia paliw g_e i mocy silnika N:

Q_b = g_e N = 270 ∙17 = 4590 [g/h] = 1,275 ∙ 10^-3 [kg/s ].

2. Obliczam wydatek masowy powietrza wykorzystując nadmiar

powietrza λ:

3. Przeliczam wydatki masowe Q na objętościowe V:

- dla benzyny:

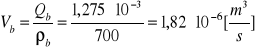
, ( 1 )

- dla powietrza:

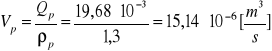
. ( 2 )

4. Średnicę dyszy paliwowej d wyznaczyłem z wydatku objętościowego V_b:

przekształcając go ze względu na d :

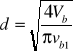
, ( 3 )

gdzie v_b1 - prędkość wypływu benzyny z dyszy paliwowej .

5. Niewiadomą prędkość
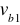
   określiłem stosując dwukrotnie równanie Bernoulliego : raz dla przekrojów 0-0 i 1-1- dla benzyny , drugi raz dla 1-1 i 2-2 - dla powietrza ( rozpatrywane przekroje zaznaczyłem na rys 1) :

1. Równanie Bernoulliego dla przekrojów 0-0 i 1-1 ( czynnik- benzyna ) ma postać:

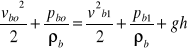
. (4)

Zakładam, że

= 0 - ze względu na dużą powierzchnię i stały poziom paliwa w

komorze pływakowej ,

= 101325 [Pa] - ciśnienie atmosferyczne,

P_b1 =p_p1 - ciśnienie na wylocie z dyszy paliwowej.

Uwzględniając ww. założenia, równanie (4) przekształciłem ze względu na

prędkość
:

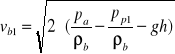
. (5)

2. W równaniu (5) występuje niewiadome ciśnienie p_p1, które wyznaczam z równania Bernoulliego napisanego dla przekrojów 1-1 i 2-2 ( czynnik-powietrze) :

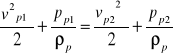
. (6)

Biorąc pod uwagę, że:

- ze względu na dużą powierzchnię wlotu w porównaniu z

przekrojem gardzieli,

- ciśnienie atmosferyczne,

równanie (6) przekształcam ze względu na p_p1 do

postaci:

. (7)

Prędkość
wyliczam z wydatku objętościowego powietrza V_p (wzór (3)):

. (8)

Po podstawieniu danych

.

Na podstawie wzoru (7) ciśnienie p_p1 w przekroju 1-1 wynosi:

3. Otrzymaną wartość ciśnienia p_p1 wstawiam do równania (5) i obliczam

.

6. Ostatecznie średnicę d dyszy paliwowej otrzymuję ze wzoru (3) po podstawieniu danych:

.

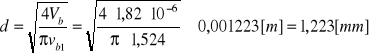
Zadanie 3

Wyznaczyć nominalny wydatek wody napływającej na łopatki wirnika turbiny Peltona oraz

- obliczyć nominalną średnicę dyszy wypływowej (d_o) ;

- obliczyć siłę naporu wody na łopatki turbiny.

1. Dane i założenia

H = 110 m - wysokość spadu wody,

N = 130 kW - nominalna moc turbiny,

- nominalna wartość współczynnika

prędkości turbiny ,

u m/s - obwodowa prędkość łopatek turbiny,

v m/s - prędkość wody wypływającej z dyszy

β = 16 ^o - kąt rozwarcia łopatek turbiny,

r = 0,6 m - promień turbiny,

ρ = 1000 kg/m³ - gęstość wody,

Q = ? m³/s - wydatek wody wypływającej z dyszy

( podlegający obliczeniu ),

d_o = ? m ( mm ) - średnica dyszy wypływowej ( podlegająca

obliczeniu ).

Obliczenia przeprowadziłem przy następujących założeniach :

- rozkład prędkości w przekroju poprzecznym strugi jest równomierny,

- ruch cieczy jest ustalony,

- pomijam lepkość cieczy ( wodę traktuję jako ciecz doskonałą )

- nie występują żadne straty energii przepływu.

Schemat działania turbiny Peltona przedstawia rys.1.

Rys.1

2. Obliczenia

1. Obliczam prędkość wypływu wody z dyszy ze wzoru Torricellego

po podstawieniu danych

[ m /s ]. (1)

2. Obliczam prędkość obwodową łopatki wykorzystując współczynnik

, stąd

3. Obliczam siłę naporu wody F działającą na łopatkę ze wzoru

czyli
(2)

4. Określenie nominalnej średnicy dyszy wylotowej

Średnicę d_o wyliczyłem, przekształcając wzór na wydatek wody wypływającej z dyszy:

gdzie A =
- przekrój wylotowy dyszy w m,

v = 46,46[m/s] - prędkość wypływu wody z dyszy ( wg. wzoru ( 1 ) ).

Ostatecznie
(3)

Problem sprowadza się do określenia wydatku Q .

3. Określenie wydatku Q wody napływającej na łopatki turbiny .

Wykorzystałem w tym celu zmianę pędu strugi wody na wlocie na łopatkę i na spływie z niej, co wywołuje powstanie siły naporu wody na łopatkę R w funkcji wydatku Q .

Schemat łopatki turbiny Peltona z naniesionymi prędkościami i siłami przedstawia rys.2.

Rys 2

Strumień wypływającej z dyszy wody o wydatku Q wpływa stycznie na zakrzywioną powierzchnię łopatki z prędkością względną w . Zakładam, że wydatek dzieli się symetrycznie po Q/2 na każdą czaszę łopatki. Łopatka odchyla strumienie o
kąt(180^o - β ).

W przyjętym układzie współrzędnych xy rzuty prędkości względnych na wlocie i spływie z łopatki z uwzględnieniem jej prędkości unoszenia u, równej prędkości obwodowej na średnicy podziałowej D= 2r wirnika będą wynosić:

- na wlocie łopatki pkt.1 (rys.2):

,

- na spływie z łopatki pkt.2 (rys.2):

;

- na spływie z łopatki pkt.3 (rys.2):

;

Napór wody na każdą czaszę łopatki (odpowiednio 1-2 i 1-3) równa się różnicy pędu początkowego i końcowego wody. W rzutach na osie :

- na oś x:

,

,

- na oś y:

,

przy założeniu, że wydatek Q dzieli się symetrycznie po Q/2 na każdą czaszę t.zn.

Q = Q/2 + Q/2 ,

Pracę użyteczną wykonuje jedynie składowa R_x będąca sumą równań (4):

R_x= R_x1-2 + R_x1-3 =
(6)

o zwrocie prędkości unoszenia u.

Składowe R_y1-2 i R_y1-3 (wg. (5)) nie wykonują pracy gdyż ich suma równa się zeru ( mają taką samą wartość, ale zwroty przeciwne). Wpływa na to symetryczny względem osi x układ powierzchni zakrzywionych (czasz) łopatki.

Praca użyteczna w jednostce czasu wyrazi się, jako R_x ∙ u _i jest równa zadanej mocy N:

.

Stąd ostatecznie otrzymałem wzór na wydatek wody wypływającej z dyszy:

.

Po podstawieniu danych:

.

Mając wartość wydatku Q ze wzoru (3) wyliczyłem średnicę dyszy d_o:

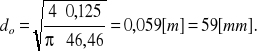
Zadanie 4

Wyznaczyć moc pompy wyporowej tłoczącej wodę do zbiorników wieżowych.

Sprawdzić czy w instalacji nie powstaje kawitacja. Schemat instalacji według rysunku.

1. Dane i założenia

Parametry instalacji hydraulicznej:

Q = 57 dcm³ / s = 0,057 m³/s - wydatek pompy

d = 260 mm = 0,26 m - średnica rurociągu,

h₁ = 1,7 m

h₂ = 6,5 m

h₃ = 22 m - wysokości pompowania,

h₄ = h₃ = 22 m

l₁ = 31 m

l₂ = 110 m

l₃ = 210 m - długości rurociągu / odcinki proste /,

l₄ = 5 l₂ = 5 ∙ 110 = 550 m

l₅ = l₃ = 210 m

ρ = 1000 kg/ m ³ - gęstość wody,

ξ_f= 5, ξ_k = 0,25, ξ_z = 0,55 - bezwymiarowe współczynniki strat

ξ_t = 2∙ ξ_k = 0,5 lokalnych, kolejno dla:filtra - f, kolana -k,

zaworu - z, trójnika - t,

λ, λ_A , λ_B - bezwymiarowy współczynnik oporu

wewnętrznego: λ_A dla gałęzi A, λ_B dla

dla gałęzi B,

p_min= 15 kPa - ciśnienie zabezpieczające przed

parowaniem wody w warunkach

normalnych (aby nie wystąpiła kawitacja

w przewodzie ssącym),

ν = 1,0 ∙ 10^-6 m² /s - współczynnik lepkości kinematycznej

wody.

Schemat instalacji ilustruje rys. 1

2. Uwagi wstępne

Instalacja jest przeznaczona do transportu wody czyli cieczy rzeczywistej obarczonej lepkością. Z tego powodu w ruchu cieczy rzeczywistej powstają straty energii mechanicznej tzw. straty przepływu związane ze spadkiem ciśnienia na drodze przepływu.

Chcąc dla tego przypadku zastosować równanie Bernoulliego należy wprowadzić poprawkę uwzględniającą straty jednostkowej energii ciśnienia ∆p_str. .

Wysokość strat ∆ p_str zależy od energii kinetycznej strugi i wyraża się wzorem:

, ( 1 )

w którym ξ - bezwymiarowy współczynnik oporu wyznaczany doświadczalnie ,o wartości zróżnicowanej w zależności od elementów składowych i konfiguracji instalacji , v- prędkość przepływu. Rozróżniamy:

1. straty liniowe (l) dotyczące prostych odcinków rur, dla których współczynnik oporu:

gdzie λ jest współczynnikiem oporu wewnętrznego, natomiast l -długością rury, a d- jej średnicą.

Jak wykazały doświadczenia . wartość współczynnika λ zależy od liczby Reynoldsa

(niemianowana) i chropowatości wewnętrznej powierzchni rury(badania Nikuradse).

Liczbę Reynoldsa określa się ze wzoru:

W instalacjach wodociągowych z reguły występuje ruch turbulentny Re>> 2340.

W moim przypadku przyjąłem więc, że ruch wody jest turbulentny ,a jako przewody-

nowe rury stalowe ciągnione gładkie.

Istnieje wiele wzorów określających wartości współczynnika λ dla rur gładkich w funkcji liczby Reynoldsa. Najpopularniejszym jest wzór Blasiusa:

(2)

(z niego będę korzystał ).

2. straty miejscowe ( m ) zachodząc na elementach składowych instalacji łączących proste odcinki rur w całość instalacji .Elementami takimi są : filtry, kolana, zawory, zasuwy, zwężki itp.

3. Przy obliczaniu jednostkowej energii straconej w instalacji ( lub jej gałęzi ) sumujemy wszystkie straty liniowe i miejscowe:

(3)

4. Podstawowym warunkiem określenia strat energii na poszczególnych elementach składowych instalacji jest znajomość prędkości przepływu wody w ich przekrojach.

Taki też przyjąłem tok postępowania: w pierwszej kolejności określiłem prędkości w poszczególnych odcinkach instalacji, następnie określiłem straty na tych odcinkach i znając te wartości, po wprowadzeniu ich do równania Bernoulliego wyznaczyłem jednostkowy (na 1 kg cieczy) wymagany przyrost energii ciśnienia ∆p jaki musi zapewnić pompa.

Na tej podstawie obliczyłem moc użyteczną pompy ze wzoru:

[k W ], (4)

natomiast moc pobraną przez pompę ( moc znamionową, moc na wale pompy ) ze wzoru

[ kW ] . (5)

We wzorach: Q [m³/s ] -wydatek pompy ,

∆p [J/kg] -jednostkowy przyrost energii ciśnienia w pompie ,

ρ = 1000 kg/m³ -gęstość wody ,

η_o -sprawność ogólna pompy; dla pomp wyporowych

waha się od 0,55 do 0,9 (dane z literatury

technicznej).

3. Obliczenia

1. Ustalam średnią prędkość przepływu wody przez pompę wychodząc ze wzoru :

. (6)

Stąd

. (7)

Jest to prędkość wody w nie rozgałęzionej części instalacji

2. Określam prędkość wody w nie rozgałęzionej częściach A i B instalacji

( w przekrojach za trójnikiem ) v_A i v_B z warunku :

Q = Q_A + Q_B ,czyli A∙ v = A ∙ v_A + A∙ v_B gdzie A - przekrój rury.

Ponieważ instalacja wykonana jest z rur o stałej średnicy (d = const.,to i A= const ).

A więc

v = v_A+ v_B (8)

3. Uwzględniając uwagi sformułowane w pkt.2. dotyczące ustalenia strat przepływu (w szczególności wartości współczynników λ_{A i} λ_B) muszę wyznaczyć prędkości przepływu v_A i v_B w rozgałęzieniach A i B.

W tym celu wykorzystuję równanie Bernoulliego:

- dla odgałęzienia A rozpatruję przekroje t - t (poziom odniesienia) i 3 - 3:

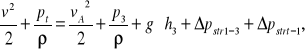
(9)

- dla odgałęzienia B rozpatruję przekroje t - t (poziom odniesienia) i 4 - 4 :

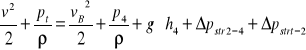
(10)

(rozpatrywane przekroje zaznaczyłem na rys. 1.) .

Jednostki wchodzące do równań Bernoulliego[(9) i (10) i dalsze] są wyrażone w jednostkach energii jednostkowej przypadającej na 1 kilogram masy cieczy:

Wobec równości lewych stron równań (9) i (10) porównuję ich prawe strony.

Przyjmuję jednocześnie, że na odcinku prostym
oraz, że w przekrojach 3-3 i 4-4 panuje ciśnienie atmosferyczne p₃=p₄ =p_a a ich położenie

h₃= h₄(wg danych z zadania ).

Warunki te prowadzą do równania:

, (11)

Po rozpisaniu strat w poszczególnych rozgałęzieniach przekształciłem równanie

(11 ) do postaci.

= 0 , (12)

które wraz z zależnością:

v = v_A+v_B

pozwoli mi na wyznaczenie współczynników λ_A i λ_B w gałęziach A i B.

4. Nie mogąc z góry określić właściwych wartości współczynników oporu λ_A i λ_B do czego potrzebna jest znajomość liczby Reynoldsa, której nie obliczę nie znając prędkości (v_A i v_B) obliczenia przeprowadziłem rachunkiem kolejnych przybliżeń. W tym celu założyłem przybliżone wartości λ_A i λ_{B ,} i obliczyłem pierwsze przybliżone wartości v_A i v_B .Według znalezionych w ten sposób prędkości określiłem liczby Reynoldsa charakteryzujące przepływ w poszczególnych odcinkach instalacji i wykorzystując wzór Blasiusa (2) ,obliczyłem wartości drugiego przybliżenia współczynników λ_A i λ_B. Drugie przybliżenie uznałem za zadawalające(z dokładnością do trzeciego miejsca po przecinku).Natomiast wartość współczynnika λ dla nie rozgałęzionej części instalacji wyznaczyłem bezpośrednio z równania Blaziusa(2) po obliczeniu liczby Reynoldsa:

;

Wyniki obliczeń zestawiłem w tablicy 1.

Przybliżenie	v	vA	vB	Re	ReA	ReB	λ	λA	λB
Pierwsze	1,074	0,636	0,438	279240	165360	113880	0,014	0,020	0,022
Drugie	1,074	0,712	0,364	279240	184600	94640	0,014	0,016	0,017

Tablica 1.

Obliczenia potwierdziły przyjęte założenia co do charakteru ruchu wody w instalacji: ruch ten jest we wszystkich gałęziach turbulentny (R_e>>2340).

5. Wyznaczam przyrost jednostkowej energii ciśnienia wytwarzanego przez pompę ∆p_pom z bilansu energetycznego dla zadanej instalacji.

W tym celu piszę równania Bernoulliego (oznaczenia zgodne z rys.1):

- dla przekrojów 0-0 i I-I:

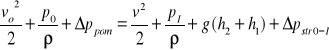
, (13)

- dla przekrojów I-I i 1-1:

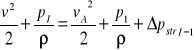
stąd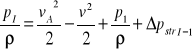
. (14)

- dla przekroju 1-1 i 3-3:

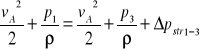
stąd
(15)

Po uwzględnieniu równań (14) i (15) oraz, że

v₀ = 0 -wobec dużej powierzchni zbiornika dolnego w porównaniu

z przekrojem rury,

p₀ = p_a + ρg h₁ -ciśnienie na poziomie 0 - 0 (gdzie, p _a = 101325 Pa -

ciśnienie atmosferyczne w warunkach normalnych),

v = v_A +v_B -prędkość wody w nierozgałęzionej części instalacji

pompowej,

równania (13) i przyjmie ostateczną postać:

, (16)

gdzie
.

6. Określam straty przepływu ∆p_strat na poszczególnych odcinkach instalacji: podstawiam dane liczbowe i wartości λ i λ_A z tablicy 1.(z drugiego przybliżenia):

- dla odcinka 0-1(część nierozgałęziona prędkość przepływu v):

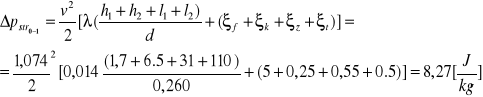
- dla odcinka 1-3 (gałąź A-prędkość przepływu v_A)

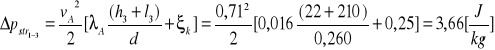
Otrzymane wyniki podstawiam wraz z pozostałymi danymi do równania (16) i obliczam przyrost energii, jaki musi dać pompa:

4. Wyznaczenie mocy pompy

Moc użyteczną pompy N_u obliczam ze wzoru (8):

,

natomiast moc pobraną przez pompę (moc na wale pompy) N_w ze wzoru (5)

Sprawność ogólną pompy η₀ = 0.8 przyjąłem na podstawie danych z literatury technicznej.

Na podstawie PN dobrałem silnik napędowy- elektryczny trójfazowy o mocy:

N_s = 22[ kW].

5. Sprawdzenie czy w instalacji nie wystąpi zjawisko kawitacji.

Najbardziej narażonym miejscem gdzie może wystąpić kawitacja jest przekrój s-s

(w króćcu ssącym pompy). Aby to sprawdzić obliczyłem w tym przekroju ciśnienie i porównałem z wartością ciśnienia zabezpieczającego przed parowaniem wody w warunkach normalnych p_min = 15 kPa (zgodnie z warunkami zadania). W tym celu napisałem równanie Bernoulliego dla przekrojów 0-0 i s-s:

(17)

Obliczam straty przepływu na odcinku 0 - s rurociągu:

Równanie (17) przekształciłem ze względu na ciśnienie p_s biorąc pod uwagę

:

,

gdzie: p_a =101325 Pa - ciśnienie atmosferyczne w warunkach normalnych.

Po podstawieniu danych otrzymałem minimalne ciśnienie na wlocie do pompy( w króćcu ssącym pompy) przy danej konfiguracji rurociągu ssawnego:
W rezultacie obliczone ciśnienie p_s jest wyższe od dopuszczalnego ciśnienia minimalnego p_min = 15 kPa

Wniosek:

Nie ma więc zagrożenia wystąpienia kawitacji w króćcu ssawnym pompy.

- 4 -

Oznaczenia:

Ω - wnętrze obszaru,

∂Ω - powierzchnia ograniczająca obszar Ω,

ds - elementarny wycinek powierzchni ∂Ω,

dv - elementarny wycinek wnętrza obszaru Ω,

f_p - jednostkowa siła powierzchniowa,

f_v - jednostkowa siła objętościowa,

n - wektor normalny do wycinka ds,

б^T_n - wektor naprężeń.

Oznaczenia:

Ω - wnętrze obszaru,

∂Ω - powierzchnia ograniczająca obszar Ω,

dv - elementarny wycinek wnętrza obszaru Ω,

ds - elementarny wycinek powierzchni ∂Ω,

n - wektor normalny do wycinka ds,

V - pole prędkości,

f_v - pole sił objętościowych,

б - pole naprężeń,

p - pole ciśnień,

P - pole gęstości pędu,

J_p - gęstość prędkości pędu,

б^T_n - wektor naprężeń,

J_p^T_n - wektor prędkości unoszenia pędu(prądu

konwekcyjnego),

ρ - gęstość płynu,

r - promień lini prądu

gdzie:

v - prędkość przepływu

[m/s ] ,

d - średnica [m],

ν - współczynnik lepkośći

kinematycznej [m²/s ],

(4)

(5)

---