Gr.24A	Wykonali: Herbuś Mariusz Miśta Tomasz		Laboratorium z mechaniki ogólnej
Ćw. nr 1	Moment bezwładności i moment dewiacji
Ocena		Data	Podpis

1.Cel ćwiczenia :

Celem ćwiczenia jest obliczenie momentu bezwładności elipsy i momentu dewiacji prostokąta.

2.Definicja momentu bezwładności i momentu dewiacji :

Momentem bezwładności ciała materialnego względem osi nazywamy sumę iloczynów elementarnych mas ciała i kwadratów ich odległości od osi.

W trójwymiarowym prostokątnym układzie współrzędnych x, y, z , mamy:

m

m v

m v

m V

m v

Momentem dewiacji ciała materialnego nazywamy sumę iloczynów elementarnych mas ciała i dwóch wybranych współrzędnych .

Zatem:

m v

m v

m v

3.Rusunek elipsy dla , której będzie liczony moment bezwładności:

y

a=9

b=2

b

-a a x

-b

4.Obliczenia całki wyznaczającej moment bezwładności elipsy :

Wzór na elipsę:

Po przekształceniu :

Analogicznie:

a). moment bezwładności elipsy względem osi ox:

Dla μ =1 całka przyjmuje postać :

b) moment bezwładności elipsy względem osi oy:

Dla μ=1 całka przyjmuje postać :

5.Program liczący wartość całki z punktów 4a i 4b.

Program moment_bezwladnosci_elipsy;

type fx=function(x:extended):extended;

type gy=function(y:extended):extended;

Var

n,st:integer;

a,a1,b,b1,eps:extended;

Function f(x:extended):extended;

begin

f:=sqrt((1-sqr(x)/81)*4)*sqrt((1-sqr(x)/81)*4)*sqrt((1-sqr(x)/81)*4)*2/3;

end;

Function g(y:extended):extended;

begin

g:=sqrt((1-sqr(y)/4)*81)*sqrt((1-sqr(y)/4)*81)*sqrt((1-sqr(y)/4)*81)*2/3;

end;

{$i simpsmpl.pas}

Begin

writeln('Program ten służy do obliczenia momentu bezwładności elipsy');

writeln;

writeln('Współrzędna x elipsy zmienia sie od -a=-9 do a=9');

writeln('Współrzędna y elipsy zmienia sie od -b=-2 do b=2');

writeln;

a1:=-8.999999;

a:=8.999999;

b1:=-1.999999;

b:=1.999999;

eps:=1e-16;

n:=6;

writeln ('Moment bezwładności względem osi ox wynosi `); writeln(`Ix:=',simpsonsimple(a1,a,f,eps,n,st));

writeln (`Obliczenia są poprawne jeśli st=0');

writeln (' st=',st:2);

writeln ('Moment bezwładności względem osi oy wynosi'); writeln(`Iy:=',simpsonsimple(b1,b,g,eps,n,st));

writeln (`Obliczenia są poprawne jeśli st=0');

writeln (' st=',st:2);

End.

6. Obliczenia momentów bezwładności elipsy wg wzorów:

1. względem osi ox :

2. względem osi oy:

7. Rysunek prostokąta dla którego wykonano obliczenia momentu dewiacji:

y

y '

b

a=2

b=6

x

a x `

8. Obliczenia całki wyznaczającej moment dewiacji prostokąta względem

osi x'y':

Dla μ=1 całka przyjmuje postać :

9. Program liczący wartość całki z punktu 8.

Program moment_dewiacji_prostokata;

type fx=function(x:extended):extended;

Var

n,st:integer;

a,b,eps:extended;

Function f(x:extended):extended;

begin

f:=18*x;

end;

{$i simpsmpl.pas}

Begin

writeln ('Program ten służy do obliczania momentu dewiacji prostokąta');

writeln ('Współrzędna x zmienia sie od 0 do a=2');

writeln ('Współrzędna y zmienia sie od 0 do b=6');

writeln;

a1:=0;

a:=2;

eps:=1e-16;

n:=6;

writeln ('Moment dewiacji prostokąta wynosi D:=',simpsonsimple (a1,a,f,eps,n,st));

writeln (' Obliczenia są prawdziwe jeśli st=0');

writeln (`st=',st:3);

End.

10. Obliczenia momentu dewiacji prostokąta wg wzoru :

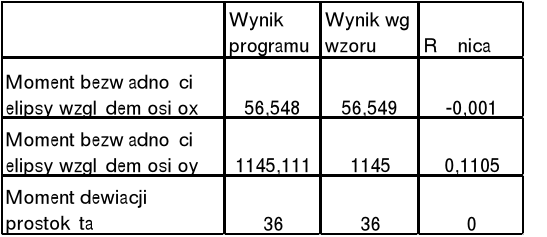
11. Zestawienie wyników;

12. Wnioski:

Przy obliczaniu momentu bezwładności za pomocą komputera otrzymuje się przybliżoną wartość tego momentu . Wynika to z ograniczeni liczby obliczeń w programie wykonującym to zadanie (zmienna n) ,oraz przybliżonej wartości granic całkowania , które mają bezpośredni wpływ na wynik obliczeń .

Przy deklaracji granic całkowania bez przybliżenia wartość momentu dewiacji obliczonego przy pomocy komputera jest równa wartości obliczonej metodą arytmetyczną wg wzoru.

1

6

---