ĆWICZENIE 1
Zaprojektować przekrój prostokątny belki żelbetowej zginanej:
pojedynczo zbrojony
podwójnie zbrojony
Nazwisko |
Temat „a” |
Temat „b” |
||||
Berek Roman |
Msd [kNm] |
Klasa bet. B |
Klasa stali A- |
Msd [kNm] |
Klasa bet. B |
Klasa stali A- |
|
279,5 |
20 |
II |
698,75 |
20 |
II |
TEMAT „a”
1.Przyjęcie danych i założeń:
- klasa ekspozycji XC3
- wytrzymałość obliczeniowa fcd=10,6MPa
- graniczna plastyczność stali fyd=310 MPa
- graniczna wartość ![]()
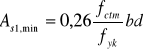
![]()
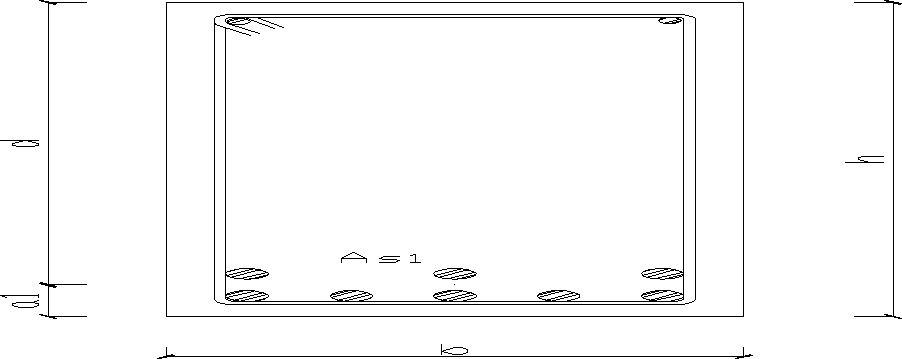
b- średnia szerokość strefy rozciąganej
d- wysokość użyteczna przekroju
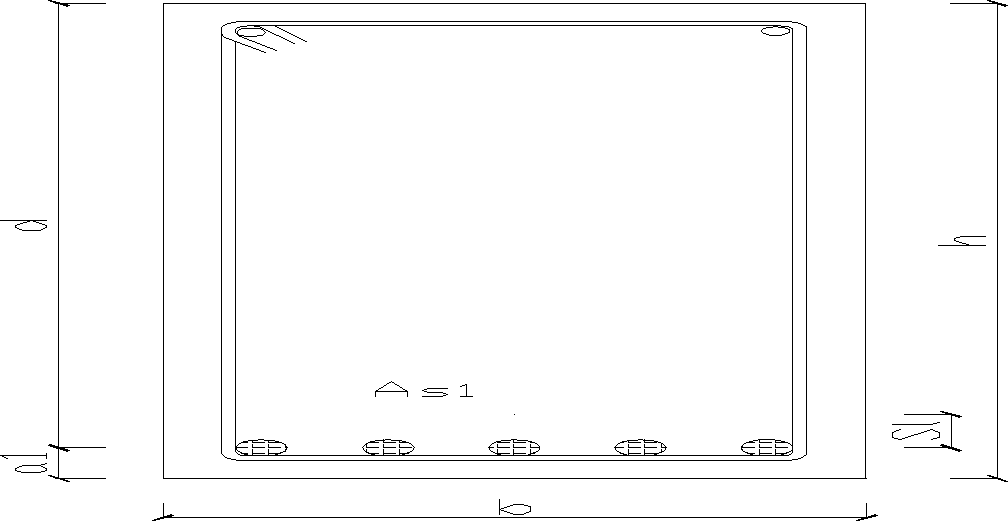
b= 30cm=300mm=0,3m
h= 60cm=600mm=0,6m
-średnia wytrzymałość betonu na rozciąganie fctm=1,9 MPa
-charakterystyczna granica plastyczności stali fyk= 355 MPa

2.Odległość osi ciężkości zbrojenia rozciąganego od najbliższej krawędzi przekroju:
![]()
3.Wysokość użyteczna przekroju:
![]()
4.Współczynnik:
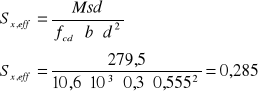
5.Względna efektywna wysokość strefy ściskanej przekroju:
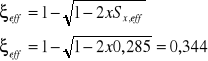
Sprawdzenie warunku:
![]()
-warunek spełniony
6.Graniczne położenie umownej osi obojętnej w przekroju:
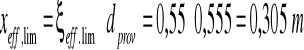
7.Łączne pole przekroju podłużnego zbrojenia rozciąganego:
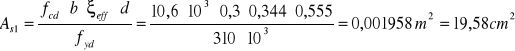
![]()
![]()
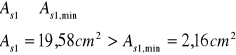
Przyjęto pręty ![]()
-8 pręty ![]()
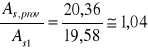

8.SPRAWDZENIE WARUNKU NOŚNOŚCI
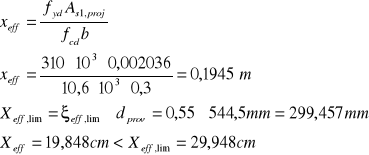
9.Nośność obliczeniowa przekroju na zginanie:

TEMAT: „b”
1.Przyjęcie danych i założeń:
Msd=698,75 kNm
Klasa betonu B-20
Klasa stali A-II
-wytrzymałość obliczeniowa fcd=10,6 MPa
-graniczna plastyczność stali fyd=310 MPa
-graniczna wartość ![]()
-średnia wytrzymałość betonu na rozciąganie fctm=1,9 MPaa
-charakterystyczna granica plastyczności stali fyk=355 MPa
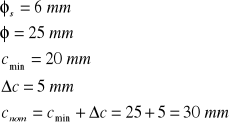
2.Odległość osi ciężkości zbrojenia As1 od rozciąganej krawędzi przekroju.
![]()
3.Odległość osi ciężkości zbrojenia As2 od rozciąganej krawędzi przekroju.
![]()
4.Wysokość użyteczna przekroju:
![]()
5.Graniczne położenie umownej osi obojętnej w przekroju:
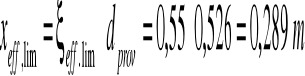
6.Moment zginający obciążający składowy przekrój 1:
![]()
7.Moment zginający obciążający składowy przekrój 2:
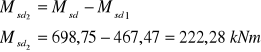
8.Pole przekroju zbrojenia ściskanego w składowym przekroju 2:
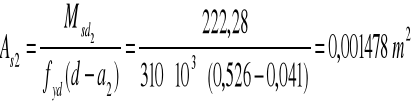
Przyjęto 5 pręty ![]()
As2,prov = 15,71cm2
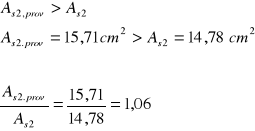
9.Współczynnik:
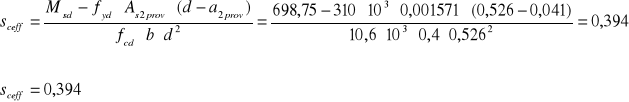
10.Względna efektywna wysokość strefy ściskanej przekroju:
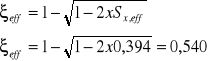
Sprawdzenie warunku:
![]()
-warunek spełniony
11.Położenie umownej osi obojętnej w przekroju:
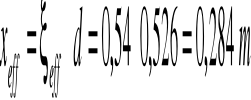
12.Pole przekroju zbrojenia rozciąganego w składowym przekroju 1:
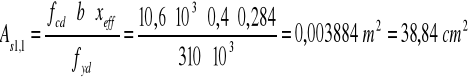
13.Pole przekroju zbrojenia rozciąganego w składowym przekroju 2:
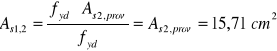
14.Całkowite pole przekroju zbrojenia rozciąganego w przekroju rzeczywistym:
![]()
Przyjmuję 12 prętów ![]()
As1,prov = 58,91cm2
(po 6 prętów w pierwszej i drugiej warstwie,)
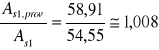
14.Odległość osi ciężkości zbrojenia od rozciąganej krawędzi przekroju:
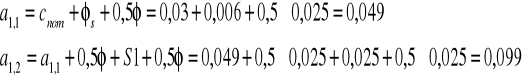
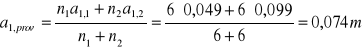

Korekta obliczeń jest zbędna
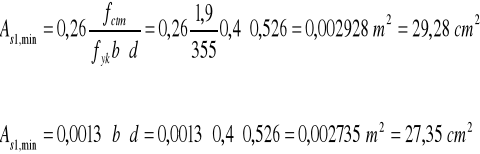
As1,prov = 0,005891m2>As1,min = 29,28cm2
Więc:
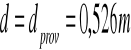
15.Położenie umownej osi obojętnej w przekroju:
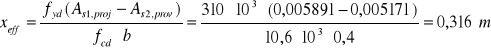
16.Graniczne położenie umownej osi obojętnej w przekroju :
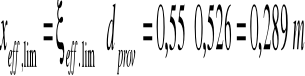
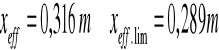
Do sprawdzenia nośności obliczeniowej przekroju na zginanie obliczam przyjmując
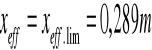
17.Nośność obliczeniowa przekroju na zginanie:
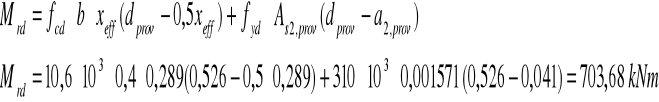
![]()
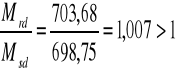
TEMAT: „c” - przekrój rzeczywiście teowy pojedyńczo zbrojony:
Msd = 765 kNm
Beton klasy B-25
Klasa stali A-III
-graniczna wartość ![]()
- wytrzymałość obliczeniowa fcd=13,3 MPa
- graniczna plastyczność stali fyd=350 MPa
-średnia wytrzymałość betonu na rozciąganie fctm= 2,2 MPa
-charakterystyczna granica plastyczności stali fyk= 410 MPa
h=700 mm=0,7m
bw=450 mm=0,45m
l0=4,5 m
hf=70 mm=0,07m
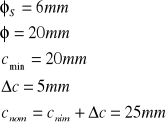
![]()
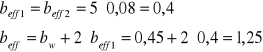
1.Odległośc osi ciężkości zbrojenia As1 od rozciąganej krawędzi przekroju:
![]()
2.Wysokość użyteczna przekroju:
![]()
3. Moment przenoszony przez półkę przekroju teowego pojedynczo zbrojonego:
![]()
![]()
Msd=765 kNm > Msd,f= 702,905 kNm
Dalsze obliczenia prowadzę jak dla przekroju rzeczywiście teowego
4. Moment obciążający przekrój składowy 2:
![]()
5. Moment obciążający przekrój składowy 1:
![]()
6.Współćzynnik dla składowego przekróju 1:
![]()
7.Względna efektywna wysokość strefy ściskanej przekroju:
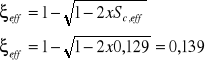
![]()
8.Pole przekroju zbrojenia rozciąganego w przekroju składowym 1:
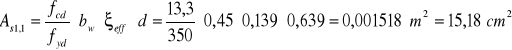
9.Pole przekroju zbrojenia rozciąganego w przekroju składowym 2:
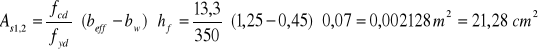
10.Łączne pole zbrojenia rozciąganego :
![]()
Przyjęto 12 prętów ![]()
w 2 rzędach o łącznym polu ![]()
(w 1 rzędzie 10 prętów, w 2 rzędzie 2 pręty)
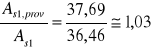
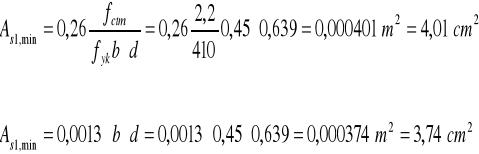
As1,prov = 37,69cm2>As1,min = 3,74cm2
11.Odległość osi ciężkości zbrojenia od rozciąganej krawędzi przekroju:
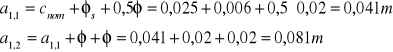
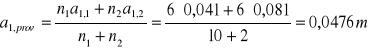

Korekta obliczeń jest zbędna więc
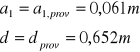
12.Sprawdzam warunek przy uwzględnieniu As2prov=0
![]()
![]()
Ponieważ lewa strona tego warunku jest większa od prawej, dalsze obliczenia prowadzę jak dla przekroju rzeczywiście teowego.
13.Położenie umownej osi obojętnej w przekroju przy przyjęciu As2prov=0
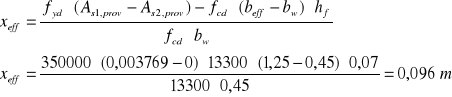
![]()
![]()
![]()
- warunek jest spełniony
14.Nośność przekroju składowego 1:
![]()
15.Nośność przekroju składowego 2:
![]()
16.Obliczeniowa nośność całego przekroju teowego na zginanie:
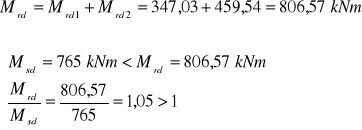
warunki nośności zostały spełnione - przekrój poprawnie zaprojektowany
ĆWICZENIE 2
TEMAT:
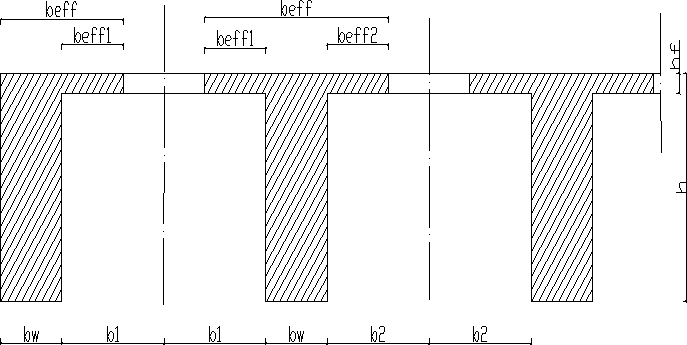
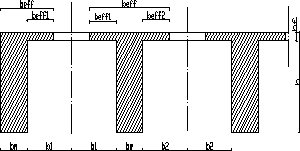
W stropie jak na szkicu zaprojektować belkę wewnętrzną w następujących obszarach:
w obszarach przekroju krytycznym (środkowym) belki obliczyć pole przekroju dolnego zbrojenia rozciąganego
rozciąganego w strefie przypodporowej zaprojektować zbrojenie na ścinanie
Nazwisko |
ba [m] |
ln [m] |
hf[m] |
Qd+∆dg [m] |
Klasa bet. B |
Klasa stali A- |
Roman Berek |
3,0 |
6,8 |
0,06 |
10,5 |
15 |
III |
„TEMAT A”
1.Przyjęcie danych i założeń:
Klasa betonu B 15
Klasa stali A - III
Średnica strzemion ![]()
= 6mm
Średnica zbrojenia ![]()
= 20mm
Grubość pułki hf = 0,06m
Wysokość przekroju h = 0,5m
Szerokość przekroju bw = 0,25m
![]()
z tab. 2 PN dla klasy betonu B15
fcd = 8,0 MPa
z tab. 3 PN dla klasy stali zbrojeniowej A - III
fyd = 350 MPa
z tab. 9 PN dla klasy stali zbrojeniowej A - III
ξeff,lim = 0,53
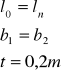
2.Wyznaczenie wysokości użytecznej przekroju:
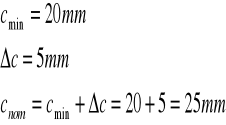
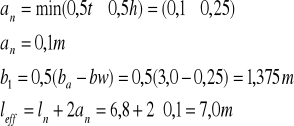
3.Wyznaczenie sił wewnętrznych:
- w przekroju z półką :
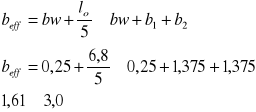
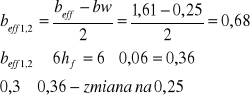
a1 = cnom + ![]()
+![]()
+ 0,5![]()
= 0,025 + 0,006 +0,02+ 0,5 · 0,02 = 0,061m
Wysokość użyteczna przekroju wynosi:
d = h - a1 = 0,5 - 0,061 = 0,439m
4.Wyznaczenie szerokości efektywnej pułki przekroju teowego:
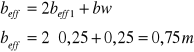
5. Sprawdzenie warunku nośności:
![]()
![]()
241,82kNm![]()
147,24kNm -ponieważ Msd![]()
Msd.f , dalsze obliczenia prowadzimy
jak dla przekroju rzeczywiście teowego pojedynczo
zbrojonego
![]()
![]()
![]()
6.Siły wewnętrzne wynoszą:
![]()
![]()
7.Obliczenie momentu przenoszonego przez przekrój składowy 1 oraz pole przekroju zbrojenia rozciąganego w tym przekroju:
-moment obciążający przekrój składowy 2
![]()
![]()
-pole przekroju zbrojenia rozciąganego w przekroju składowym 2
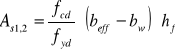
![]()
8.Obliczenie momentu przenoszonego przez przekrój składowy 1 oraz pole przekroju zbrojenia rozciąganego w tym przekroju:
-moment obciążający przekrój składowy 1
![]()
![]()
-współczynnik dla składowego przekroju 1
![]()
![]()
-względną efektywną wysokość strefy ściskanej przekroju
![]()
-pole przekroju zbrojenia rozciąganego w przekroju składowym 1
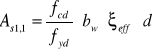
![]()
9.Określenie liczby prętów w zbrojeniu rozciąganym:
-łączne pole przekroju zbrojenia rozciaganego
![]()
![]()
Przyjęto 7 prętów o średnicy 20mm i łącznym polu przekroju ![]()
; 5 prętów w dolnej warstwie i 2 w drugiej

Korekta obliczeń jest zbędna.
Sprawdzenie warunku: ![]()
21,99cm2 > 1,44 cm2 - warunek spełniony
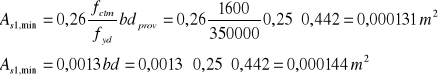
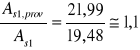
10.Sprawdzenie nośności:
a) Sprawdzenie warunku:
![]()
![]()
![]()
Warunek nie jest spełniony, co oznacza ze umowna oś obojętna znajduje się w obrębie środnika a przekroju jest przekrojem teowym (dalsze obliczenia jak dla przekroju rzeczywiście teowego).
-położenie umownej osi obojętnej w przekroju;
![]()
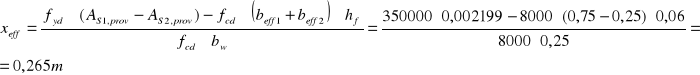
-graniczne położenie umownej osi obojętnej w przekroju;
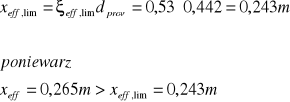
W dalszych obliczeniach przyjmuję ![]()
-nośność przekroju składowego 1
![]()
- nośność przekroju składowego 1
![]()
![]()
-obliczeniowa nośność całego przekroju teowego na zginanie
![]()
![]()
![]()
„TEMAT B”
Dane podstawowe:
Liczba ramion strzemion nw1 = 4
Średnica strzemion φs = φ1 = 6mm
Średnica zbrojenia φ = φ2 = 20mm
Kąt nachyleni strzemion odgiętych α = 90°
Maksymalna siła tnąca VSd 138,18= kN
Maksymalny moment zginający MSd = 241,82 kNm
Grubość pułki hf = 0,06m
Wysokość przekroju h = 0,5m
Szerokość przekroju bw = 0,25m
1.Wyznaczenie sił krawędziowych:
![]()
![]()
2.Obliczenie w przekrojach miarodajnych stopnia ![]()
:
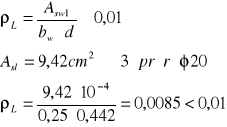
3. Wyznaczenie potrzebnych współczynników:
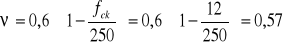
Ponieważ do podpory doprowadzono mniej niż 50% zbrojenia rozciąganego to k = 1.
Ponieważ w rozpatrywanym przekroju nie występuje siła osiowa wówczas powstałe naprężenia σcp = 0kN.
4.Wyznaczenie nośności ze względu na rozciąganie betonu nieuzbrojonego na ściskanie:
![]()
![]()
5.Wyznaczenie nośności ściskanych krzyżulców betonowych:
![]()
![]()
![]()
6.Wyznaczenie w strefach przypodporowych rozpatrywanego przęsła elementu odcinków pierwszego rodzaju:
![]()
![]()
![]()
![]()
-warunek nie został spełniony (odcinki ścinania drugiego rodzaju)
wymagane jest zbrojenie poprzeczne
7.Wytypowanie odcinków elementu żelbetowego (odcinki ścinania drugiego
rodzaju):
![]()
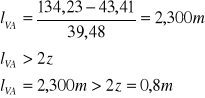
- odcinek drugiego rodzaju dzielimy na mniejsze odcinki:
Dzielę powyższy odcinek na 4 części a zatem:
![]()
przyjmuję:
![]()
Sprawdzenie warunku:
![]()
![]()
![]()
- warunek spełniony
8.Obliczenie nośności betonowych krzyżulców na ściskanie:
![]()

Sprawdzenie warunku:
![]()
![]()
- warunek spełniony
9.Wyznaczenie łącznego pola przekroju nw1:
Dla średnicy strzemion φ1 = 6mm całkowite pole przekroju wynosi:
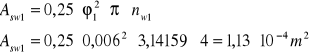
Jako klasę stali na strzemiona przyjmuję A - 0 dla której fyd = 190MPa
fyk = 220MPa
a zatem fywd1 = 190MPa
10.Wyznaczanie poszczególnych pododcinków:
10.1.Wyznaczanie rozstawu strzemion:
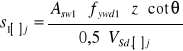
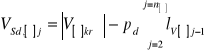
-dla pododcinka ![]()
![]()
![]()
do dalszych obliczeń przyjmuję ![]()
- dla pododcinka ![]()
![]()
![]()
do dalszych obliczeń przyjmuję ![]()
- dla pododcinka ![]()
![]()
![]()
do dalszych obliczeń przyjmuję ![]()
- dla pododcinka ![]()
![]()
![]()
do dalszych obliczeń przyjmuję ![]()
10.2.Sprawdzenie stopnia zbrojenia strzemionami:
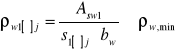
gdzie:
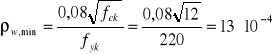
- dla ![]()
![]()
![]()
![]()
- warunek spełniony
- dla ![]()
![]()
![]()
![]()
- warunek spełniony
- dla ![]()
![]()
![]()
![]()
- warunek spełniony
- dla ![]()
![]()
![]()
![]()
- warunek spełniony
10.3.Wyznaczenie maksymalnego dopuszczalnego rozstawu strzemion:
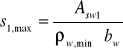
![]()
![]()
![]()
<![]()
![]()
<![]()
![]()
<![]()
![]()
<![]()
- warunki spełnione
10.4.Sprawdzenie warunku:
![]()
![]()
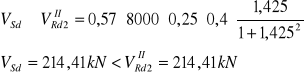
- warunek spełniony
10.5.Sprawdzenie ilości zbrojenia rozciąganego w miarodajnym przekroju na początku rozpatrywanego pododcinka:
W rozpatrywanym pododcinku występują 3 pręty w strefie rozciąganej
![]()
Łączne wymagane pole przekroju wynosi:
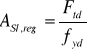
gdzie:
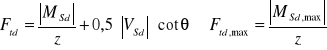
![]()
![]()
![]()
![]()
![]()
![]()
Pręty w przekroju 1 są w stanie przenieść siłę ![]()
zatem:
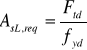
![]()
10.6.Sprawdzenie ilości zbrojenia:
![]()
![]()
-warunek niespełniony
Ponieważ pręty rozciągane ![]()
nie są w stanie przenieść siły ![]()
w związku z tym przedłużam do podpory jeszcze 2 pręty otrzymując ![]()
o ![]()
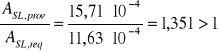
-warunek spełniony
oraz przedłużam poza ten przekrój na odległość co najmniej równą ![]()
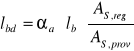
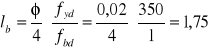
![]()
![]()
![]()
![]()
10.7.Sprawdzenie stanu granicznego zarysowania:
10.7.1.Wyznaczenie całkowitego stopnia zbrojenia:
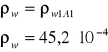
10.7.2.Obliczenie granicznej wartości siły poprzecznej:
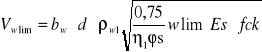
Dla przyjętych klasy ekspozycji XC1 graniczną szerokość rozdarcia rys wynosi ![]()
Moduł sprężystości dla stali ![]()
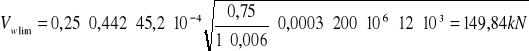
Zgodnie z założeniami do projektu przyjmuje ![]()
a zatem siła poprzeczna wynosi:
![]()
Obciążenie charakterystyczne wynosi:
![]()
10.7.3.Sprawdzenie warunku granicznego zarysowania:
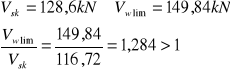
Warunek spełniony
ĆWICZENIE 3
Temat:
Zaprojektować prostokątny przekrój smukłego (η = 1) słupa żelbetowego o długości lcol mimośrodowo ściskanego występującego w ustroju o węzłach nie przesuwnych jako słup n-tej kondygnacji licząc od góry(występując w monolitycznym ustroju szkieletowym).
Zakres ćwiczenia:
- zwymiarować zbrojenie As1 i As2
- wyznaczyć nośność NRd i sprawdzenie normowego warunku nośności
NSd [kN] |
ee [m] |
lcol [m] |
Klasa betonu B |
Klasa stali A |
n |
2850 |
0,025 |
7,5 |
15 |
III |
3 |
1.Przyjęcie danych i założeń:
Klasa betonu B 15
Klasa stali A - III
Średnica strzemion φs = 6mm
Średnica zbrojenia φ = 20mm
Klasa ekspozycji: Xo
Es: 200Gpa
Ecm: 30Gpa
lo=lcol: 7,5m
cmin 20mm
![]()
5mm
![]()
2,0
Wysokość przekroju h = 0,6m
Szerokość przekroju bw = 0,3m
![]()
z tab. 2 PN dla klasy betonu B15
fcd = 8,0 MPa
z tab. 3 PN dla klasy stali zbrojeniowej A - III
fyd = 350 MPa
z tab. 9 PN dla klasy stali zbrojeniowej A - III
ξeff,lim = 0,53
2. Odległość osi ciężkości zbrojenia As1 od rozciąganej krawędzi przekroju:
a1 = cmin + Δc +φs +0,5Sl = 0,02 + 0,005 + 0,006 +0,5 · 0,02 = 0,041 m
3. Odległość osi ciężkości zbrojenia As2 od ściskanej krawędzi przekroju:
a2 = cmin + Δc +φs + 0,5φ = 0,02 + 0,005 + 0,006 +0,5 · 0,02 = 0,041 m
4. Nie zamierzmy mimośród przypadkowy:
![]()
![]()
5. Mimośród konstrukcyjny:
![]()
6. Wyznaczenie mimośrodu początkowego:
![]()
![]()
Ponieważ smukłość elementu ![]()
Zatem uwzględniam w obliczeniach wpływ tej smukłości. Sprawdzam warunek:
![]()
7.Współczynnik uwzględniający długotrwałość obciążenia:
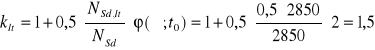
8.Moment bezwładności przekroju betonu:
![]()
9.Moment bezwładności przekroju całej stali zbrojeniowej przyjmuje w przybliżeniu jako:
![]()
10. Siła krytyczna:
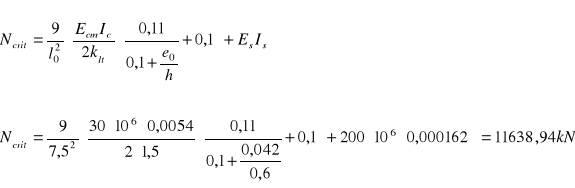
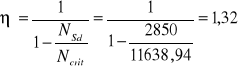
11.Mimośród całkowity:
![]()
12.Wysokość użyteczna przekroju:
![]()
13.Położenie osi ciężkości elementu:
![]()
14.Mimośród siły podłużnej:
![]()
![]()
15.Pole przekroju zbrojenia ściskanego:
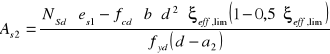
![]()
Przyjmuję 11 prętów ![]()
w 1 pierwszej warstwie 6 prętów i 2 warstwie 5 pręty, o łącznym polu:
![]()
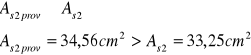
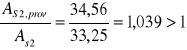
16.Pole przekroju zbrojenia rozciąganego:
Ponieważ:
![]()
Więc:
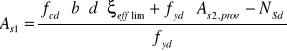
![]()
Po wstępnym przyjęciu przypadku dużego mimośrodu i przeprowadzeniu dla takiego przypadku obliczeń otrzymałem As1 <0, co świadczy o tym, że mam do czynienia z przypadkiem małego mimośrodu, w związku z tym dalsze obliczenia przeprowadzam jak dla mimośrodu małego.
17.Pole przekroju zbrojenia rozciąganego lub mniej ściskanego:
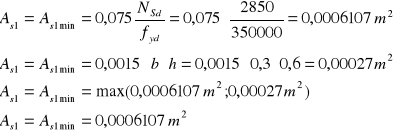
;
Przyjmuje 2 pręty o średnicy 20mm w jednej warstwie o łącznym polu przekroju
As1,prov= 6,28cm2 a1,prov=a1=0,041m oraz dprov=h-a1prov=0,6-0,041=0,559m I obliczam dalej.
18.Wielkość pomocnicza:
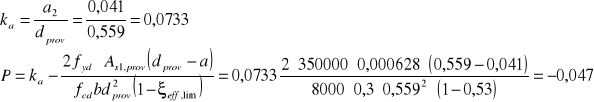
19.Względna efektywna wysokość strefy ściskanej:
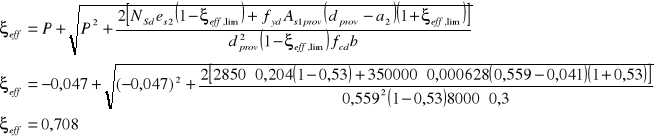
Ponieważ ![]()
, to stwierdzam, że zachodzi odmiana I mimośrodowego ściskania na małym mimośrodzie i dla tej odmiany wyznaczam współczynnik:
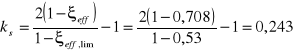
20.Pole przekroju zbrojenia ściskanego:
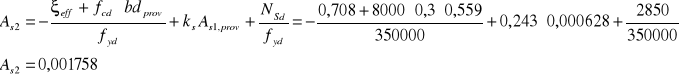
Przyjmuję 6 prętów ![]()
w 1 jednym rzędzie, o łącznym polu:
![]()
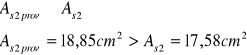
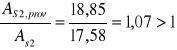
21.Sprawdzenie pola przyjętego zbrojenia:
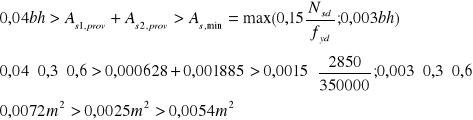
Warunek spełniony
22.Względna efektywna wysokość strefy ściskanej:
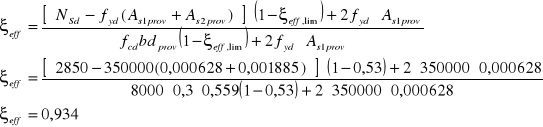
23.Nośność przekroju na zginanie przy mimośrodowym ściskaniu na małym mimośrodzie:
![]()
, stwierdzam, że zachodzi odmiana I mimośrodowego ściskania na małym mimośrodzie i dla tej odmiany wykonuje obliczenia wg wzoru:
![]()
![]()
![]()
![]()
![]()
Warunek spełniony
24.Nośność przekroju ze względu na siłę podłużną ściskającą na małym mimośrodzie:
Obliczam kolejno współczynniki potrzebne do obliczenia nośności przekroju:
-współczynnik:
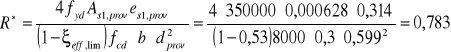
-współczynnik:
![]()
-współczynnik:
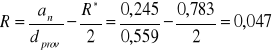
-Względna efektywna wysokość strefy ściskanej
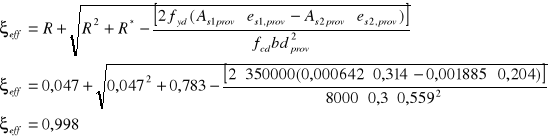
Ponieważ ![]()
, stwierdzam, że zachodzi odmiana I mimośrodowego ściskania na małym mimośrodzie i najpierw dla tej odmiany wyznaczam współczynnik:
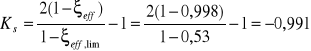
-Nośność ![]()
przekroju:
![]()
![]()
![]()
Sprawdzenie warunku:
![]()
-warunek spełniony
36
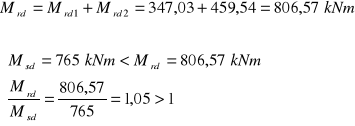
Wyszukiwarka
Podobne podstrony:
ĆWICZENIE-BaJu-dobry, NAUKA, budownictwo, Semestr V, konstrukcje betonowe, Żelbet
Semestr 4-zagadnienia egzaminacyjne-2011, PŁ, Budownictwo, 4 semestr, Konstrukcje Betonowe, Beton 2
OPIS TECHNICZNY ZE STALI, NAUKA, budownictwo, Semestr V, Konstrukcje stalowe, Projekt - Szczurek
egz bet I term 111, pk budownictwo, Semestr 7, KONSTRUKCJE BETONOWE
betony - odpowiedzi, Studia PG Budownictwo, BUDOWNICTWO, SEMESTR V, KONSTRUKCJE BETONOWE, Egzamin
Faza I przed zarysowaniem, PŁ, Budownictwo, 4 semestr, Konstrukcje Betonowe, Beton 2, Wykład
ZADANIE1, budownictwo, semestr V, konstrukcje betonowe, ćwiczenia
Nosnosc przekroju w paszczynie X, PŁ, Budownictwo, 4 semestr, Konstrukcje Betonowe, Beton 1
Konstrukcje betonowe I - egzamin, PŁ, Budownictwo, 4 semestr, Konstrukcje Betonowe, Beton 2
Politechnika Białostocka, budownictwo, semestr5, Konstrukcje Betonowe, Projekt, Przodek inne, Refera
projekt stal dobry, NAUKA, budownictwo, Semestr V, Konstrukcje stalowe, Projekt - Szczurek
Konstrukcje betonowe I - egzaminbbababab, PŁ, Budownictwo, 4 semestr, Konstrukcje Betonowe, Beton 2
KM ODPOWIEDZI (1), WST Katowice Budownictwo, V semestr, Konstrukcje betonowe
3.4 opisbadbeton, NAUKA, budownictwo, BUDOWNICTWO sporo, Diamentowa, Konstrukcje betonowe, Zelbet la
3.2 op bamodułuspr, NAUKA, budownictwo, BUDOWNICTWO sporo, Diamentowa, Konstrukcje betonowe, Zelbet
opis tech zelbet 1, Budownictwo UTP, rok II, semestr 4, Konstrukcje Betonowe, strop
3.3 opisbadstali, NAUKA, budownictwo, BUDOWNICTWO sporo, Diamentowa, Konstrukcje betonowe, Zelbet la
próbek walcowych, NAUKA, budownictwo, BUDOWNICTWO sporo, Diamentowa, Konstrukcje betonowe, Zelbet la
więcej podobnych podstron