Zadanie nr 3

Jacek Gruszka

Zbiór zadań z matematyki i rachunku prawdopodobieństwa dla kierunku: Energetyka

I. Repetytorium z matematyki

1. Oblicz a)
; b)
c)
d)

2. Rozwiązać w zbiorze liczb zespolonych równanie:

a) x² - 4x +13 = 0; b) x² - 4x +13 = 0; c) z²+ (2-j)z - 2j =0;

d)
, f)

3. Obliczyć macierz odwrotną do danej macierzy metodą przekształceń elementarnych:

a)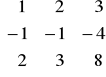
b)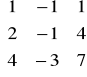
c)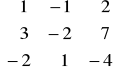

d)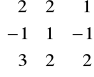
e)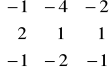
f)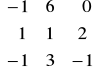

g)
h)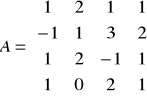

4. Wyliczyć wyznaczniki:

a)
b)
c)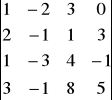
d)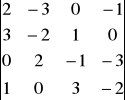

e)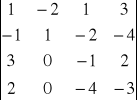
f)
g)
h)

5. Wyliczyć rząd macierzy:

a)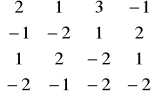
; b)
; c)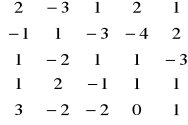
;

6. Rozwiązać układ równań metodą eliminacji Gaussa:

a)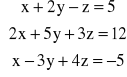
b)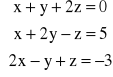
c)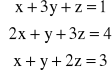
d)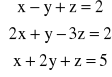

e)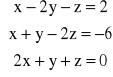

f)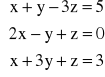
g)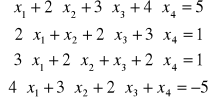
,

h)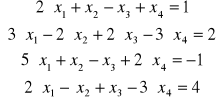
i)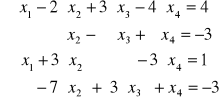

8) Obliczyć pochodną funkcji:

a)
; b)
; c)
; d)
; e)
; f)
;

g)
; h)
; i)
; j)
; k)
.

9) Obliczyć granicę funkcji:

1. 
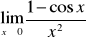
   ; b)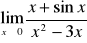
   ; c)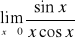
   ; d)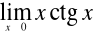
   ; e)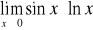
   ;

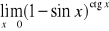
6. 
   ; g)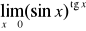
   ; h)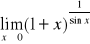
   i)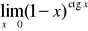
   ; j)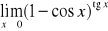
   ;

k)
; l)
; m)
; n)

10) Zbadać monotoniczność funkcji:

1. 
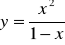
   ; b)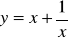
   ; c)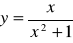
   ; d)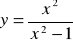
   ; e)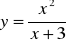
   ; f)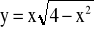
   ;

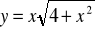
7. 
   ; h)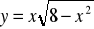
   ; i)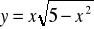
   ; j)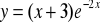
   ; k)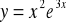
   ;

; m)
.

11) Obliczyć wartości ekstremalne funkcji:

a)
; b)
; c)
; d)
; e)
;

f)
; g)
; h)
.

12) Obliczyć całkę

a)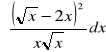
; b)
; c)
; d)
; e)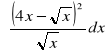
; f)
; g)
; h)
; i)
;

j)
; k)
; l)
; m)
; n)
; o)
; p)

14) Obliczyć pole obszaru płaskiego ograniczonego liniami:

a)
; b)
;

c)
; d)
;

e)
; f)
;

g)
; h)
;

i)
.

15) Znaleźć wartości ekstremalne funkcji z = f(x,y):

1. z = 2x² + y² - xy - 3x - y ; b) z = x² + 2y² + xy - 3x - 5y ;

c) z = x² + 2y² - xy - x - 3y d) z = - x² - 3y² + 2xy + 4y ;

e) z = x² + y² - 5xy + 4x + 4y ; f) z =
·x³ +
·x² + xy - 2x - 2y ;

g) z =
·x³ +
·y³ - xy ; h) z = x² + y³ - xy - x - 2y + 1 ;

i) z = x³ + y² - 4xy + x +2y +1; j) z = ln (9 - x² - y²) ; k) z = x·e^{x + y˛} ;

l) z = y·e^{x˛ + y}; m) z = e^{x˛ + 2y˛} .

16) Wyznacz gradient funkcji skalarnej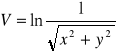
w punkcie P = (1,-2).

17) Wylicz całkę podwójną: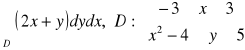
.

18) Wylicz pochodną kierunkową funkcji
w punkcie P = (2,
) w

kierunku wektora
.

19) Wylicz różniczkę zupełną funkcji
.

20) Wyznaczyć rozwiązanie ogólne równania różniczkowego:

a)
; b)
; c)
;

21) Stosując transformację Laplace'a wyznaczyć rozwiązanie szczególne równania

różniczkowego, spełniające podane warunki:

a)
; b)
.

II. Rachunek prawdopodobieństwa

1) Z urny, w której są 3 kule białe i pewna liczba kul czarnych, wybieramy losowo dwie kule.

Ile może być wszystkich kul w urnie, jeżeli prawdopodobieństwo wybrania przynajmniej

jednej kuli białej jest większe od 0,5?

2) Partię towaru liczącą 50 sztuk poddaje się losowej kontroli. Jeżeli z dwóch wybranych

losowo sztuk co najmniej jedna jest wadliwa, partię odrzucamy, w przeciwnym przypadku

przyjmujemy. Co jest bardziej prawdopodobne przy takiej kontroli : odrzucenie partii

zawierającej 4% sztuk wadliwych, czy przyjęcie partii zawierającej 70% sztuk wadliwych?

3) Prawdopodobieństwo zapalenia ognia pojedynczą zapałką wynosi 0,6 ; a dwiema

zapałkami na raz 0,9. W pudełku są dwie zapałki. Jak należy postąpić przy zapalaniu, aby

prawdopodobieństwo zapalenia ognia było większe?

4) Prawdopodobieństwo trafienia celu przynajmniej raz przy trzech niezależnych strzałach

wynosi
. jakie jest prawdopodobieństwo trafienia celu przy jednym strzale?

5) Z urny zawierającej 4 kule białe i 5 czerwonych usuwamy losowo jedną kulę, a następnie

wybieramy losowo dwie kule. Co jest bardziej prawdopodobne : wybranie dwóch kul

białych pod warunkiem, że usunęliśmy kulę czerwoną, czy wybranie dwóch kul o różnych

kolorach, pod warunkiem, że usunęliśmy kulę białą?

6) Średnio pięciu mężczyzn na stu i dwie kobiety na tysiąc nie rozróżniają kolorów. Z grupy,

w której stosunek liczby kobiet do liczby mężczyzn wynosi 3:7 wybrano losowo jedną

osobę. Oblicz prawdopodobieństwo zdarzenia, że wybrana osoba nie rozróżnia kolorów.

7) W każdym z dwóch pudełek jest po 10 losów. W jednym pudełku są 2 losy wygrywające,

a w drugim 3 wygrywające. W jaki sposób wybrać dwa losy z pudełek, aby mieć

największą szansę, że oba będą wygrywające, jeżeli :

1. wiemy, w którym pudełku są 2, a w którym 3 losy wygrywające,

2. nie wiemy, w którym pudełku są 2, a w którym 3 losy wygrywające.

8) Z urny zawierającej 3 kule białe i 4 czerwone wybieramy losowo 6 razy po dwie kule,

przy czym za każdym razem wylosowaną parę kul wrzucamy z powrotem do urny. Oblicz

prawdopodobieństwo :

1. trzykrotnego wylosowania pary kul tego samego koloru,

2. przynajmniej pięciokrotnego wylosowania pary kul o różnych kolorach.

9) W urnie znajduje się 6 kul białych i 4 czarne. Wybieramy losowo 5 razy po dwie kule,

zwracając za każdym razem wybraną parę do urny. Jakie jest prawdopodobieństwo

zdarzenia, że dokładnie trzy razy wylosujemy parę kul o różnych kolorach?

10) W fabryce produkowane są detale na maszynach A, B i C. Na maszynie A

wyprodukowano 200 detali, średnio 4% wadliwych, na maszynie B - 300 detali, średnio

5% wadliwych, na maszynie C - 400 detali, średnio 2% wadliwych. Całodzienną

produkcję złożono do pojemnika. Z pojemnika wylosowano jeden detal, który okazał się

wadliwy. Jakie jest prawdopodobieństwo, że zostal on wyprodukowany na maszynie A ?

11) Firma składająca komputery zaopatruje się w procesory u trzech dostawców A, B i C

dostarczających, odpowiednio, 25%, 35% i 40% zamawianych procesorów. Wadliwość

dostarczanych procesorów pochodzących od tych dostawców wynosi, odpowiednio, 5%,

4% i 2%. Sprawdzono losowo jeden z dostarczonych procesorów, który okazał się

wadliwy. Jakie jest prawdopodobieństwo, że pochodził on od dostawcy C ?

12) Przeprowadzone badania wykazały, że co dziesiąty student dojeżdża na zajęcia własnym

samochodem. Jakie jest prawdopodobieństwo, że wśród 200 losowo wybranych

studentów co najmniej 17, ale nie więcej, niż 24 dojeżdża na zajęci własnym

samochodem ?

13) Wśród studentów studiów niestacjonarnych 70% ma stałą pracę. Obliczyć

prawdopodobieństwo, że wśród 200 losowo wybranych studentów studiów

niestacjonarnych, stałą pracę ma co najmniej 135, ale nie więcej, niż 150.

14) W pewnym zakładzie pracy oszacowano koszty poniesione na unowocześnienie parku

maszynowego (x_i) i uzyskane w związku z tym przychody (y_i). W kolejnych czterech

latach dane te przedstawiają się następująco:

Metodą najmniejszych kwadratów wyznacz prostą regresji liniowej, oszacuj

dopasowanie parametrów i przy pomocy wartości krytycznych rozkładu t - Studenta

przy założonym poziomie istotności ά = 0,1, określ, czy zmienne są istotne.

6

xi	1	3	4	5
yi	3	6	7	8

---