2. Rachunek zbiorów

Pojęcie zbioru traktujemy jako pojęcie pierwotne, tzn. przyjmujemy je bez definicji.

PODSTAWOWE RELACJE MIĘDZY ZBIORAMI:

1. A ⊂ B- Inkluzja zbiorów (zawieranie się zbiorów, zbiór A jest podzbiorem zbioru B) (A ⊂ B) ⇔ (a ∈ A ⇒ a ∈ B) (def.)

2. A=B- Równość zbiorów A = B ⇔ (a ∈ A ⇔ a ∈ B) (def.)

DZIAŁANIA NA ZBIORACH:

1. A ∪ B -Suma zbiorów(złączenia zbioru) a ∈ (A ∪ B) ⇔ (a ∈ A ∨ a ∈ B) (def.)

2. A ∩ B -Iloczyn zbiorów (część wspólna, przekrój zbiorów) a ∈ (A ∩ B) ⇔ (a ∈ A ∧ a ∈ B) (def.)

3. A \ B -Różnica zbiorów a ∈ (A \ B) ⇔ (a ∈ A ∧ a ∉ B) (def.)

4. A ÷ B -Różnica symetryczna zbiorów (A ÷ B) = (A \ B) ∪ (B \ A) (def.), (A ÷ B) = (A ∪ B) \ (A ∩ B) (własność)

5. A` - Dopełnienie (uzupełnienie) zbioru (a ∈ A` ) ⇔ (a ∉ A) ⇔ ∼(a ∈ A) (def.), A` = ж \ A (def.) , gdzie ж - przestrzeń.

3. Zbiory liczbowe.

Sekwencja inkluzji zbiorów liczbowych: N⊂C⊂W⊂R∈Z.

1. N - zbiór liczb naturalnych: N={1, 2, 3, ...}. Indukcyjność zbioru liczb naturalnych (1∈N) ∧[(n∈N)=>(n+1) ∈N)]

2. C - zbiór liczb całkowitych: C = N∪{0}∪PN, gdzie PN={c; c∈N}- zbiór liczb przeciwnych do liczb naturalnych.

3. W - zbiór liczb wymiernych - to zbiór wszystkich możliwych ilorazów liczb całkowitych tzn.

W={
;
=C1/C2 ∧ (C1∈C) ∧ (C2∈C) ∧ (C2
0)}

4. R - zbiór liczb wymiernych: R = W∪NW, gdzie NW to zbiór liczb niewymiernych.

5. Z - zbiór liczb zespolonych: Z = R ∪U, gdzie U to zbiór liczb urojonych

1. postać ogólna liczby zespolonej: Z = a + b⋅i, gdzie: a, b∈R, a=Re(Z)-część rzeczywista liczby zespolonej Z, b=Im(Z)-część urojona liczby zespolonej Z, i =
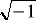
   - jednostka urojona(nie rzeczywista).Jeżeli b=0 =>Z=a∈R, Jeżeli b
   0=>Z=a+b⋅i∈U. WOBEC TEGO: Z=R∪U

2. Postać trygonometryczna liczby zespolonej:

PŁASZCZYZNA ZESPOLONA

Punkt o współrzędnych(a,b) na płaszczyźnie zespolonej będzo,będziemy identyfikować z liczbą zespoloną Z = a + b⋅i, przy czym r =
= z - moduł liczby zespolonej z, tzn.(długość promienia wodzącego).

sinφ=b/r =>b=r⋅ sinφ

cosφ=a/r =>a=r⋅ cosφ

Z= r (cosφ + i⋅sinφ) Postać trygonometryczna liczby zespolonej, gdzie φ=Arg(z) jest argumentem liczby zespolonej Z to znaczy katem nachylenia promienia wodzącego r do osi rzeczywistej Re

3)Działania na liczbach zespolonych:

1. Dodawanie liczb zespolonych

Z1= a1 + b1⋅i

Z2 = a2 + b2⋅i

Z1+Z2=(a1+a2)+(b1+b2)⋅i ∈Z

2. Odejmowanie liczb zespolonych(tak jak dodawanie)

3. Mnożenie liczb zespolonych

Z1⋅ Z2=(a1+a2⋅i) ⋅ (a2⋅a2⋅i)=a1⋅a2+b1⋅a2⋅i+a1⋅b2⋅i⋅b1⋅i^2=(a1⋅a2-b1⋅b2)+(a1⋅b2_a2⋅b1) ⋅ i ∈Z

4. Dzielenie liczb zespolonych

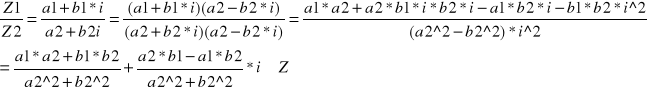
5. Potęgowanie liczb zespolonych: Z= r (cosφ + i⋅sinφ), Zⁿ -n-ta potęga liczby zespolonej Z,

Zⁿ = rⁿ [cos(nφ) + i·sin(nφ)]. Oznacza to że potęgowanie liczby zespolonej Z sprowadza się do potęgowania modułu i mnożenia argumentu przez stopień, czyli: Zⁿ=zⁿ = rⁿ , Arg(zⁿ⁾ = n⋅ Arg(z) = nφ

6. Pierwiastkowanie liczb zespolonych: Z= r (cosφ + i⋅sinφ),

Wzór MOIURE'a:
= z_k =
(cos
+ i⋅sin
) dla k= 0,1,2,...n-1

4. Relacje i odwzorowania.

1.Pojęcie relacji: Każdy nie pusty podzbiór iloczynu kartezjańskiego dwóch zbiorów stanowi pełną relację pomiędzy elementami tych zbiorów, przy czym: *mówimy o relacji pomiędzy elementami zbiorów A i B <=>, gdy jest to niepusty podzbiór iloczynu kartezjańskiego AxB(relacja w szerszym sensie tzn sensulargo), *mówimy o relacji określonej w zbiorze A <=>, gdy jest to niepusty podzbiór iloczynu kartezjańskiego AxA=A^2(relacje w węższym sensie sensustricto)

2.Pojęcie odwzorowania: Klasyczne pojęcie odwzorowania (funkcji) jest następujące: Jeżeli każdemu elektowi ze zbioru A przyporządkowany jest dokładnie jeden element zbioru B to mówimy o odwzorowaniu A w zbiór B.

Pojęcie odwzorowanie można także traktować jako pewną relację pomiędzy elementami zbiorów A i B spełniających warunek jednoznaczności przyporządkowanej.

Oznaczenia: b=f(a)-element b jest obrazem elementu a poprzez odwzorowanie f, przy czym: a-argument odwzorowania, b-wartość odwzorowania f, A-dziedzina odwzorowania(zbiór argumentów),
-przeciwdziedzina odwzorowania (zbiór wartości).

W ogólnym przypadku mamy f(A)=
⊂B, tzn. f jest odwzorowaniem zbioru A w zbiór B.

Jeżeli f(A)=B to mówimy o tzw. SURJEKCJI, tzn. odwzorowanie zbioru A na zbiór B.

3.Odwzorowania wzajemnie jednoznaczne i odwracanie: Mówimy, że odwzorowanie f: A→B(zbióru A w zbiór B) jest wzajemnie jednoznaczne (jedno-jednoznaczne, różnowartościowe) <=>, gdy: /\ f(a1)=f(a2)<=>(a1=a2). Oznacza to, że dla odwzorowania jednoznacznego wartości odwzorowania są równe wtedy i tylko wtedy, gdy równe są argumenty.

Mówimy, że odwzorowanie f: A→B jest odwracalne <=>, gdy istnieje odwzorowanie odwrotne
: B→A.

Odwzorowanie odwrotne
: B→A istnieje <=>, gdy odwzorowanie podstawowe f: A→B jest wzajemnie jednoznaczną surjecją, czyli jest to różnowartościowe odwzorowanie zbioru na zbiór B.

Nie jest to odwzorowanie, bo nie jest spełniony warunek jednoznaczności przyporządkowania.

Jest to odwzorowanie, które nie jest wzajemnie jednoznaczne.

Jest to odwzorowanie wzajemne jednoznaczne, ale nie jest odwracalne (nie wykorzystane b4).

Jest to odwzorowanie odwracalne tzn. wzajemnie jednoznaczna surjekcja.

5. Ciąg liczbowy i jego granica. Podstawowe własności.

Def. Ciąg liczbowy jest to odwzorowanie, które każdje liczbie naturalnej n przyporządkowujemy dokładnie jedną liczbę rzeczywistą a_n zwaną wyrazem ciągu.

Ciąg liczbowy jest funkcją, której argumentami są liczby naturalne, a wartościami są liczby rzeczywiste(wyrazy ciągu są numerowane) { a_n }- ciąg o wyrazach a_n.

UWAGA: *zgodnie z def. ciąg liczbowy jest nieskończony, ponieważ argumentami są tutaj liczby naturalne, których jest nieskończenie wiele. *Możemy pytać o granice ciągu, gdy n→ ∞.

Podstawowe własności ciągów liczbowych.

1. Monotoniczność ciągu liczbowego:

Mówimy, że ciąg jest monotoniczny ⇔ gdy

a) ٨ a_n+1 > a_n - ciąg rosnący

n∈N

b) ٨ a_n+1 < a_n - ciąg malejący

n∈N

c) ٨ a_n+1 ≥ a_n - ciąg niemalejący

n∈N

d) ٨ a_n+1 ≤ a_n - ciąg nierosnący

n∈N

2. Ograniczoność:

a) ciąg ograniczony z góry ⇔ ٧ ٨ a_n ≤ M

M∈R n∈N

b) ciąg ograniczony z dołu ⇔ ٧ ٨ a_n ≥ m

m∈R n∈N

c) ciąg ograniczony ⇔ ٧ ٨ a_n≤ M,

M>0 n∈N

3. Granica ciągu liczbowego

Definicja granicy wg Cauchy'ego jest następująca:

lim a_n = g ⇔ (٨ ٧ ٨ a_n - g < ε)

n→ ∞. ε > 0
> 0 n >

a_n - g < ε <=> - ε< a_n - g< ε <=> g- ε< a_n<g+ ε <=> a_n∈(g- ε, g+ ε)<=> a_n
(g, ε)-otoczenie punktu g o promieniu ε

Oznacza to, że liczba g jest granicą ciągu{an}<=>, gdy do
(g, ε) punktu g o promieniu ε należa prawie wszystkie wyrazy ciągu o nr n większych od dodatniej liczby
zależy od promienia otoczenia ε>0.

4.Ciągi zbieżne i rozbieżne

Jeżeli ciąg liczbowy posiada granicę zgodnie z definicją Cauchy'ego, to mówimy że jest to ciąg zbieżny, a skończoną granicę w tym przypadku nazywamy granicą właściwą.

Ciągi które nie mają granicy właściwej nazywać będziemy ciągami rozbieżnymi. Wśród ciągów rozbieżnych wyróżniamy ciągi rozbieżne do nieskończoności i mówimy wówczas, że ciąg taki ma granice niewłaściwą(+∞, bądź -∞). Ciągi które nie posiadają ani granicy właściwej ani niewłaściwej nazywamy ciągami rozbieżnymi.

6. Granice niewłaściwe ciągu liczbowego. Wyrażenia nieoznaczone.

Formalnie definicje dotyczące granic niewłaściwych ciągu liczbowego można uzyskać przez stosowną modyfikację definicji Cauchy'ego:

1.Def. granicy niewłaściwej + ∞ dla ciągu {an} domyślnie(gdy n→ ∞)

(lim a_n = +∞) ⇔ ٨ ٧ ٨ a_n > M

n→ ∞ M > 0
> 0 n >

Oznacza to że {a_n} jest rozbieżny do +∞ ⇔ gdy prawie wszystkie wyrazy tego ciągu są większe od dowolnej dodatniej liczby M.

Inaczej mówiąc: Wszystkie wyrazy ciągu liczbowego rozbieżnego do +∞ o numerach n większych od dodatniej liczny
(zależnych od M>0) są większe od dowolnie dużej dodatniej liczby M.

2.Granica niewłaściwa -∞

(lim a_n = - ∞ ) ⇔ ٨ ٧ ٨ a_n > m

n→ ∞ m > 0
> 0 n >

czyli prawie wszystkie wyrazy ciągu rozbieżnego do - ∞ są mniejsze od dowolnej ujemnej liczby m.

Wyrażeniami nieoznaczonymi

Wyznaczając praktycznie granice różnych liczbowych często będziemy mieli doczynienia z. wyrażeniami którym nie można nadać jednoznacznie wartości granicznej gdy n→ ∞.Mówimy wówczas, że jest to wyrażenie nieoznaczone, przy czym do podstawowych wyrażeń nieoznaczonych zaliczamy:

,
, ∞-∞, 0_*∞ , 0⁰ , ∞⁰ ,

7. Twierdzenia o ciągach liczbowych zbieżnych i rozbieżnych do nieskończoności.

1. Jeżeli ciąg {a_n} i {b_n} są ciągami zbieżnymi takimi, że:

lim a_n = a i lim b_n = b to wówczas:

n→∞ n→∞

1. granica sumy ciągów jest równa sumie granic tych ciągów

lim (a_n + b_n) = lim a_n + lim b_n = a + b

n→∞ n→∞ n→∞

2. granica iloczynu ciągów jest równa iloczynowi granic tych ciągów

lim (a_n * b_n) = lim a_n * lim b_n = a * b

n→∞ n→∞ n→∞

3. granica różnicy ciągów równa się różnicy granic tych ciągów

lim (a_n - b_n) = lim a_n - lim b_n = a - b

n→∞ n→∞ n→∞

4. jeżeli założymy, że wyrazy ciągu {b_n} są różne od zera oraz granica tego ciągu jest także różna od zera to wówczas:

lim (a_n / b_n) = lim a_n / lim b_n = a / b

n→∞ n→∞ n→∞

gdzie ٨ b_n ≠ 0 oraz b ≠ 0

n∈N

tzn. granica ilorazu ciągów jest równa ilorazowi granic tych ciągów.

2. Twierdzenie o trzech ciągach. Jeżeli wyrazy trzech ciągów {a_n}, {b_n}, {c_n} spełniają dwa następujące założenia:

a)٨ a_n ≤ b_n ≤ c_{n ,}

n

To znaczy prawie wszystkie wyrazy trzech ciągów(czyli począwszy od
) spełniają powyższy układ nierówności.

b) lim a_n = lim c_n = g

n→∞ n→∞

To znaczy-ciągi skrajne{a_n}, {c_n} czyli są zbieżne do tej samej granic g. To wówczas ciąg środkowy{b_n} jest także zbieżny do granicy g czyli lim b_n=g

n→∞

SCHEMAT

Twierdzenie o trzech ciągach może być także zastosowane odpowiednia dla granic niewłaściwych (+∞, bądź -∞).

3. Każdy ciąg monotoniczny i ograniczony jest zbieżny.

a) Jeżeli ciąg liczbowy jest rosnący i ograniczony z góry to jest ciągiem zbieżnym.

b) Jeżeli ciąg liczbowy jest malejący i ograniczony z doły to jest ciągiem zbieżnym.

4. Granica ciągu harmonicznego: a_n =
α > 0 (R⁺)

٨ lim
= 0

α > 0 n→∞

5. Granica ciągu wykładniczego a_n = qⁿ, gdzie q ∈ R

+∞ , gdy q > 1

lim qⁿ = 1 , gdy q = 1

n→∞ 0 , gdy q < 1

nie istnieje, gdy q ≤ -1

(c.rozbieżby)

6. Liczba e (liczba Napiera)

Liczna e jest zdefiniowana jako granica ciągu o wyrazach a_n = (1 + 1/n)ⁿ , przy czym n→∞

Jest to wyrażenie nieoznaczone typu

lim (1 + 1/n)ⁿ = e

n→∞

gdzie e jest liczbą niewymierną, która wynosi e = 2,7182..... ≈ 2,72

8. Definicja granicy funkcji jednej zmiennej (interpretacja geometryczna).

Definicja wg Heinego

Liczbę g nazywamy granicą funkcji f(x) w punkcie x₀ wtedy i tylko wtedy, gdy istnieje taka liczba δ > 0, że dla każdego ciągu punktów {x_n} należących do sąsiedztwa S(x₀, δ), zbieżnego do x₀, ciąg wartości funkcji {f(x)} jest zbieżny do granicy g, tzn.:

lim f(x) = g ⇔ ٧ ٨ lim x_n = x₀ ⇒ lim f(x_n) = g

x→x₀ δ>0 {x_n};x_n∈S(x₀,δ) n→∞ n→∞

Jeżeli funkcja f(x) ma granice w punkcie x₀ zgodnie z definicją Heine'go, to mówimy o granicy właściwej (skończonej).

INTERPRETACJA GEOMETRYCZNA

Jeżeli dowolny ciąg argumentów jest zbieżny do punktu x_0, a odpowiadający mu ciąg wartości funkcji jest zbieżny do punktu g to liczbę g nazywamy granica funkcji w punkcie x_0.

UWAGA: Istnienie granicy funkcji f(x) w punkcie x₀ nie wymaga istnienia wartości funkcji w tym punkcie.

9. Granice jednostronne i niewłaściwe funkcji jednej zmiennej(interpretacja geometryczna).

Stosowana modyfikowana def. Heinego pozwala napisać def. prawostronnej oraz lewostronnej granicy funkcji f(x) w punkcie x_0.

1. Def. (wg Heinego) prawostronnej granicy funkcji f(x) w punkcie x_0.

lim f(x) = p ⇔ ٧ ٨ lim x_n = x₀ ⇒ lim f(x_n) = p

x→x₀⁺ δ>0 {x_n};x_n∈S⁺(x₀,δ) n→∞ n→∞

Oznacza to, że liczbę p nazywamy prawostronną granicą funkcji f(x) w punkcie x₀ ⇔ gdy istnieje taka liczba δ > 0, że dla każdego ciągu argumentów {a_n}, którego wyrazy należą do prawostronnego sąsiedztwa punktu x₀ o promieniu δ, zbieżnego do x₀, ciąg wartości funkcji {f(x)} jest zbieżny do punktu p.

2. Def. lewostronnej granicy funkcji f(x) w punkcie x₀

lim f(x) =1 ⇔ ٧ ٨ lim x_n = x₀ ⇒ lim f(x_n) = 1

x→x₀^- δ>0 {x_n};x_n∈S^-(x₀,δ) n→∞ n→∞

To znaczy: dla granicy lewostronnej: dla każdego ciągu argumentów zbieżnego lewostronnie do punktu x₀ odpowiadający mu ciąg wartości funkcji jest zbieżny do liczby l.

UWAGA: Warunkiem koniecznym i dostatecznym istnienia granicy funkcji f(x) w punkcie x₀ jest istnienie i równość granic jednostronnych w danym punkcie.

To znaczy:

lim f(x) =g ⇔[l=limf(x)=g=limf(x)=p

x→x₀ x→x₀^- x→x₀⁺

10. Granice funkcji w nieskończoności (interpretacja geometryczna).

O ile dziedzina na to pozwala możemy mówić o granicy funkcji w + ∞ bądź w - ∞.

a) granica funkcji f(x) w + ∞ dla funkcji określonej w pewnym prawostronnie nieograniczonym przedziale (a; + ∞) ⊂ D

lim f(x) = g ⇔ ٨ (x_n → +∞) ⇒ [f(x_n) → g]

x→+∞ {x_n}, x_n∈(a, +∞)

Oznacza to,że liczba g jest granicą funkcji f(x) w +∞ <=>, gdy dla każdego ciągu argumentów rozbieżnego do +∞ , odpowiadający mu ciąg wartości funkcji jest zbieżny do liczby g.

INTERPRETACJA GEOMETRYCZNA

Jeżeli granica funkcji w +∞ jest właściwa (skończona) to wykres funkcji ma asymptotę poziomą prawostronną(to znaczy gdy x→+∞ )o równaniu y=g.

b) granica funkcji f(x) w - ∞ dla funkcji określonej w pewnym lewostronnie nieograniczonym przedziale (-∞; b) ⊂ D

lim f(x) = g ⇔ ٨ (x_n → -∞) ⇒ [f(x_n) → g]

x→-∞ {x_n}, x_n∈(-∞; b)

To znaczy: dla każdego argumentu rozbieżnego do-∞, odpowiadający mu ciąg wartości funkcji jest zbieżny do liczby g.

INTERPRETACJA GEOMETRYCZNA

Lewostronna asymptota pozioma o równaniu y=g (gdy x→-∞)

11. Wybrane twierdzenia o granicach funkcji.

1. Twierdzenie o trzech funkcjach.

Jeżeli trzy funkcje f(x), g(x) i w(x) określone są w pewnym sąsiedztwie S(x₀, δ) punktu x₀, Jeśli ponadto spełniają dwa założenia:

a) ٨ f(x) ≤ g(x) ≤ h(x)

x∈S(x₀, δ)

b) funkcje f(x) i h(x) posiadają te samą granicę g w punkcie x₀, tzn.

lim f(x) = lim h(x) = g

x→x₀ x→x₀

to wówczas funkcja g(x) posiada także granicę w punkcie x₀ równą g, tzn.

lim g(x) = g

x→x₀

SYMBOLICZNIE (SCHEMATYCZNIE)

UWAGA! Twierdzenie o trzech granicach dotyczy również granic jednostkowych oraz granic funkcji w nieskończoności, granic niewłaściwych w każdym z tych przypadków. Wymaga to stosownej modyfikacji założeń i tezy tego twierdzenia.

2. lim
= 1

x → 0

[o/o] tw.

Iloraz f(x)
w punkcie x₀=0 jest wyrażeniem nieoznaczonym typu [0/0], można udowodnić, wykorzystując tw. O trzech funkcjach oraz elementarne własności funkcji trygonometrycznych, że granica tego ilorazu jest równa 1.

3. Modyfikacja liczby e.

[ b_n→ (±) ∞ ] ⇒ [lim (1 +
) ^bn = e] ….[
]

n→∞

Przyjmując podstawianie: (x=
)<=>( b_n =1/x) przy czym [ b_n→ (±) ∞ ] <=> (x → 0), otrzymamy lim (1 + x)^1/x = e

x → 0

Zmodyfikowana def. liczby e w postaci granicy funkcji f(x)= (1 + x)^1/x w punkcie x₀=0, przy czym jest to wyrażenie nieoznaczone typu [
] (analogicznie jest w def. liczby e jako granicy pewnego ciągu).

12. Ciągłość funkcji jednej zmiennej. Rodzaje nieciągłości (przykłady).

Jeżeli funkcja f(x) jest określona w pewnym otoczeniu punktu x₀ oraz granica funkcji jest równa wartości funkcji w tym punkcie, to mówimy, że funkcja f(x) jest ciągła w punkcie x₀, tzn.

lim f(x) = f(x₀) -ciągłość funkcji w punkcie x₀

x→x₀

Definicja ciągłości funkcji w punkcie wymaga określoności funkcji zarówno w punkcie x₀ (prawa strona) jak i w pewnym sąsiedztwie punktu x₀ (lewa strona).

Oznacza to, że: warunkiem koniecznym ciągłości funkcji f(x) w punkcie x₀ jest jej określoność w pewnym otoczeniu punktu x_0.

Inaczej mówiąc: Jeżeli funkcja jest ciągła w punkcie x₀ to(konicznie) jest określona w pewnym otoczeniu punktu x₀. Twierdzenie odwrotne nie jest w prawdziwe, to znaczy określoność funkcji w pewnym otoczeniu punktu x₀ nie wystarczy do stwierdzenia, że funkcja jest ciągła w punkcie x₀ (określoność nie jest warunkiem dostatecznym dla ciągłości).

Można mówić o ciągłości jednostronnej funkcji f(x) w punkcie x₀ wówczas gdy istnieje właściwa granica jednostronna równa wartości funkcji w danym punkcie.

To znaczy:

a) lim f(x) = f(x₀) - prawostronna ciągłość w punkcie x₀

x→x₀⁺

b)lim f(x) = f(x₀)-lewostronna ciągłość w punkcie x₀

x→x₀^-

Rodzaje nieciągłości

Mówimy ,że x₀ jest punktem nieciągłości funkcji f(x) <=>, gdy funkcja f(x) jest określona w pewnym sąsiedztwie punktu x₀ i nie jest ciągła w tym punkcie.

Wyróżniamy dwa rodzaje punktów nieciągłości:

1. mówimy że punkt x₀ jest punktem nieciągłości pierwszego rodzaju funkcji f(x) ⇔ gdy funkcja f(x) nie jest ciągła w punkcie x₀, ale obie granice jednostronne w tym punkcie są właściwe (skończone).

2. Mówimy o nieciągłości drugiego rodzaju ⇔ gdy funkcja f(x) nie jest ciągła w punkcie x₀ oraz przynajmniej jedna z granic jednostronnych jest niewłaściwa, bądź w ogóle nie istnieje (def. komplementarna)

1)W punkcie „a” funkcja jest ciągła (granica prawostronna równa wartości funkcji w tym punkcie)

2)x1- nieciągłość pierwszego rodzaju (obie granice jednostronne są właściwe, ale brak wartości funkcji). Jest to tkz. nieciągłość usuwalna w tym sensie, że przyjmując wartość funkcji w punkcie x1 równą granicy właściwej w tym punkcie x1.

3)x2- nieciągłość pierwszego rodzaju (obie granice jednostronne są właściwe, ale różne, => brak granicy jest przyczyną nieciągłości.

4)x3-nieciągłość drugiego rodzaju (lewostronna asymptota pionowa, to znaczy lewostronna granica niewłaściwa w punkcie x3)

5)x4-nieciągłość drugiego rodzaju(obie granice jednostronne są niewłaściwe-obustronna asymptota pionowa).

6)x5-nieciągłość pierwszego rodzaju(istnieje wartość funkcji, istnieje granica właściwa, ale są różne).Jest to nieciągłość usuwalna (korekta wartości funkcji)

7)x6-ciągłość

8) W punkcie ”b” funkcja jest lewostronna ciągła(brak wartości funkcji w tym punkcie)

UWAGA! W punkcie x2 funkcja jest lewostronnie ciągła (w sensie ogólnym jest nieciągła).

13. Definicja pochodnej funkcji jednej zmiennej i jej interpretacja geometryczna.

Jeżeli istnieje właściwa granica ilorazu różnicowego funkcji f(x) w punkcie x₀, to granicę te nazywamy pochodną funkcji f(x) w punkcie x₀ i piszemy:

f '(x) = lim
=

x→x₀

lim
= lim

Δx →0 Δx →0

Definicja pochodnej ma charakter warunkowy to znaczy pochodna w punkcie x₀ istnieje tylko wówczas gdy istnieje właściwa granica ilorazu różniczkowego, przy czym iloraz różnicowy dla funkcji ciągłej jest wyrazem nieoznaczonym typu [0/0], gdy x → x₀

Analogicznie definiujemy pochodne jednostronne funkcji f(x) w punkcie x₀, zakładając że odpowiednie granice jednostronne ilorazu różnicowego w punkcie x₀ są właściwe i piszemy:

f '(x₀⁺) = lim
- pochodna prawostronna

x→x₀

f '(x₀^-) = lim
- pochodna lewostronna

x→x₀

14. Różniczka funkcji jednej zmiennej (interpretacja geometryczna).

Różniczką funkcji f(x) w punkcie x₀ dla przyrostu Δx=x- x₀ nazywamy iloczyn pochodnej f. w punkcie x₀ i przyrostu Δx.

To znaczy: dy|=f `( x₀)*Δx

| x=x₀

Ponieważ dla funkcji f(x)=x mamy dx=1*Δx zatem ogólny zapis różniczki funkcji y=f(x) jest następujący: dy=df=f `(x)*dx, gdzie dy-różniczka funkcji(zmiennej zależnej y), dx=Δx-różniczka zmiennej(równa przyrostowi argumentu x)

INTERPRETACJA GEOMETRYCZNA:

f `( x₀)=tg
(fi)- współczynnik kierunkowy stycznej

dy / _{x = x0} = tg
_* Δx=QS

Ponieważ tg
=QS/P₀S=QS/Δx

Oznacza to, że Różniczka f. w danym punkcie x₀ dla przyrostu Δx jest przybliżoną miarą faktycznego przyrostu wartości funkcji Δy odpowiadające przyrostowi argumentu Δx to znaczy dy
Δy, przy czym przybliżenie to jest tym dokładniejsze im przyrost argumentu Δx jest mniejszy.

Wówczas: Błąd względny tego przybliżenia dąży do zera, gdy Δx→0, bo:

15. Elementarne twierdzenia o funkcjach różniczkowalnych.

*Mówimy, że funkcja f(x) jest różniczkowa w punkcie , gdy istnieje pochodna funkcji w tym punkcie.

*Mówimy o różniczkowalności funkcji f(x) w przedziale otwartym(a,b) <=>, gdy funkcja jest różniczkowalna a każdym punkcie wew. Tego przedziału.

*Można mówić także o różniczkowalności funkcji w przedziale zamkniętym [a,b] wówczas, gdy przyjmiemy dodatkowo, że istnieją odpowiednie pochodne jednostronne na krańcach tego przedzialu.

To znaczy:

f `(a<sup>+</sup> ) oraz f `(b^-)

1. Ciągłość funkcji f(x) jest warunkiem koniecznym dla jej różniczkowalności w punkcie lub przedziale.

Inaczej mówiąc: Jeżeli funkcja jest różniczkowalna w punkcie x₀ (istnieje pochodna w tym punkcie) to wówczas(koniecznie) funkcja jest ciągła w punkcie x_0.

Twierdzenie odwrotne nie jest prawdziwe. To znaczy: Jeżeli funkcja jest ciągła w punkcie x₀ to nie wystarczy do stwierdzenia, że jest różniczkowalna w tym punkcie.

Oznacza to, że: Ciągłość nie jest warunkiem wystarczającym, dostatecznym dla różniczkowalności funkcji. Punkt, w którym funkcja jest ciągła, ale nie jest różniczkowalna nazywa się ostrze.

W punktach x1,x2,x3 na rysunku występuje ostrze, to znaczy funkcja jest ciągła, ale nie jest różniczkowalna, ponieważ brak stycznej w tych punktach pozwala wnioskować o braku pochodnej.

2. Jeżeli funkcje f(x) i g(x) są różniczkowalne(w punkcie lub przedziale) to suma, różnica iloraz tych funkcji są także óżniczkowalne przy czym:

a) [f(x)+g(x)]`=f `(x) + g`(x)

b) [f(x)-g(x)]`=f `(x) - g`(x)

c) [f(x)*g(x)]`=f `(x)*g(x) + f(x)*g`(x)

Jeżeli przyjmiemy dodatkowo, że g(x) ≠ 0 to iloraz f(x)/g(x) jest także różniczkowalny, przy czym:

d) [f(x)/g(x)]`= f `(x)*g(x) - f(x)*g`(x)/[g(x)]^2

3. Pochodna funkcji złożonej : f(g(x))- funkcja złożona przy czym g(x) jest funkcją wewnętrzną f(u) jest funkcją zewnętrzną, gdzie u=g(x) oraz argumentem f. zew. f(u). Jeżeli funkcja wew. G(x) jest różniczkowalna w punkcie x₀ natomiast f. zew. f(u) jest różniczkowalna w punkcie u₀=g(x) to wówczas f. złożona f(g(x)) jest różniczkowalna w punkcie x₀ przy czym

[f(g(x))]`=f `(u)*g`(x) - pochodna f. złożonej jest równa iloczynowi pochodnej f. zew. f `(u) i pochodnej f. wew. g`(x)

4.Pochodna funkcji odwrotnej. Jeżeli funkcja y = f(x) jest odwracalną funkcja różniczkowalna w przedziale (a,b) to wówczas funkcją odwrotną x = f ^-1(y) jest także różniczkowalna pochodna funkcji odwrotnej i odwrotnością pochodnej funkcji podstawowe, to znaczy: [f ^-1(y)]`=
, gdzie f `(x₀) ≠ 0(dla każdego punktu należącego do przedziału, w którym spełnione są powyższe założenia.

16. Pochodne funkcji elementarnych.

a)Funkcja potęgowa

*w wąskim sensie (sensu stricte)

f(x) = xⁿ ; gdzie n ∈ N, x ∈ R=Df

f `(x) = n ⋅ x^n-1

*w szerszym sensie (sensu largo)

f(x) = x^a , gdzie a ∈ R, x ∈ R⁺ =Df- wspólna dziedzina dla wszystkich funkcji potęgowych o stałym, ale dowolnym wykładniku a ∈ R

f `(x) = a ⋅ x^a-1

b) f. wykładnicza

f(x) = a^x, gdzie (1 ≠ a > 0), x ∈ R=Df

f `(x) = a^x ⋅ lna, gdzie lna = log_ea -jest tzw. logarytmem naturalnym o podstawie e

w szczególności:

(e^x)' = e^x ⋅ lne = e^x

c) f. logarytmiczna

f(x) = logax, gdzie (1 ≠ a > 0), x ∈ R⁺

y=log_ax<=>(def) x=a^y

(log_ax)'=
, ponieważ korzystając ze wzoru na pochodną f. odwrotnej otrzymamy: (log_ax)'=1/(a^y)`=1/a^y*lna=1/x*lna

w szczególności:

(lnx)' =

d) f. trygonometryczne

(sin x)'= cos x , gdzie x ∈ R

(cos x)'= -sin x, gdzie x ∈ R

(tg x)'=
=1 + tg²x,gdzie x ≠
(k ∈C)

(ctg x)'=
= -(1 + ctg²x), gdzie x ≠ kπ (k ∈ C)

17. Funkcje cyklometryczne i ich pochodne.

Formalnie funkcje trygonometryczne nie są odwracalne jako funkcje okresowe. Definiuje się je jednak funkcje odwrotne do f. trygonometrycznych zwane f. cyklometrycznymi przyjmując dla danej funkcji trygonometrycznej taki przedział zawarty w dziedzinie, w którym f. ta jest ściśle monotoniczne czyli różnowartościowa, tym samym odwracalna.

a)y=arcsinx <=>(def)x=siny, dla x∈[-1,1]=Darcsin, y∈[-π/2, π/2]=

Pochodna funkcji y=arcsinx zgodnie ze wzorem na pochodną f. odwrotnej przymnie postać :

gdzie x∈(-1,1)

b) y=arccosx<=>x=cosy, dla x∈[0,1], y∈[0, π]

(arccosx)`= 1/cosy`=1/-siny=-1/(1-cos^2x)=
,gdzie x∈(-1,1)

c)y=arctgx<=>x=tgy,

dla x∈R=D, y∈ [-π/2, π/2]=

Pochodna funkcji:

(arctgx)`=1/(tgy)`=1/1+tg^2y=1/1+x^2, gdzie x∈R

d)y=arcctgx<=>x=ctg, dla dla x∈R=D, y∈ [0, π]=

(arcctgx)`=1/(ctgy)`=1/-(1+ctg^2y)`=-1/1+x^2, gdzie x∈R

18. Twierdzenie Lagrange'a (interpretacja i wnioski).

Jeżeli funkcja y = f(x) jest funkcją ciągłą w przedziale [a, b] i różniczkowalna w przedziale otwartym (a; b) to wówczas istnieje taki punkt wewnętrzny przedziału (a, b), w którym pochodna opisuje tzw. wartość średnią funkcji f(x) w przedziale [a, b], tzn.

٧ f `( c) =

c∈(a; b)

Iloraz
opisuje tkz wartość średnią w tym sensie, że jest to przeciętny przyrost wartości funkcji przypadający na jednostkę argumentu w przedziale [a,b].

INTERPRETACJA GEOMETRYCZNA

= tgα - współczynnik kierunkowy siecznej

f `( c) - współczynnik kierunkowy stycznej do krzywej w punkcie c.

Zgodnie z tezą twierdzenia Lagrange'a równość f `( c) =
oznacza że istnieje w przedziale(a,b) istnieje przynajmniej jeden taki punkt wew. c, w którym styczna do wykresu funkcji jest równoległa do poprowadzonej przez punkty krańcowe przedział[a,b](punkty c1,c2 na rysunku)

Inaczej mówiąc: Jeżeli spełnione są zał tw. L.to istnieje przynajmniej jeden punkt wewnętrzny przedziału (a, b), w którym pochodna jest równa tak zwanej wartości średniej wyznaczonej przez punkty krańcowe danego przedziału.

Wnioski z twierdzenia Lagrange'a:

1. Jeżeli dla każdego x∈ (a, b) pochodna w punkcie x jest równa zero to:

٨ f `(x) = 0 ⇒ f(x) = const

x∈(a; b)

2. ٨ f `(x) > 0 ⇒ funkcja jest rosnąca w danym przedziale

x∈(a; b)

3. ٨ f `(x) < 0 ⇒ funkcja jest malejąca w danym przedziale x∈(a; b)

19. Twierdzenie de L'Hospitala.

Jeżeli spełnione są trzy następujące założenia:

a)ilorazy
oraz
są określone w pewnym sąsiedztwie punktu x₀

b)iloraz
jest wyrażeniem nieoznaczonym
lub
w punkcie x₀

c)istnieje właściwa granica ilorazu pochodnych w punkcie x₀ tzn.

lim
= a∈R

x→x₀

To wówczas istnieje granica ilorazu
w punkcie x₀ i jest równa granicy ilorazu pochodnej tzn.

lim
= lim
= a

x→x₀ x→x₀

KOMENTARZE:

1. Pierwsze założenie twierdzenia de L'Hospital'a oznacza że w sąsiedztwie punktu x₀ określona jest wartość funkcji f(x) oraz g(x) jak i ich pochodne f `(x) i g`(x) oraz g(x) ≠ 0 i g'(x) ≠ 0 w tym sąsiedztwie.

2. Drugie założenie twierdzenia de L'Hospital'a oznacza, że

lim f(x) = lim g(x) = 0 (=>[0/0]) lub

x→x₀ x→x₀

[lim f(x) =(±)∞ i lim g(x) = (±)∞] (=>
)

x→x₀ x→x₀

3.Teza tw. H. mówi o równości granicy ilorazu
i ilorazu
tylko wówczas gdy spełnione są wszystkie trzy założenia tego twierdzenia.

4. Twierdzenie H. może być zastosowane odpowiednio także dla granic jednostronnych, granic funkcji w nieskończoności oraz dla granic niewłaściwych w każdym z tych przypadków.

5. Twierdzenie de L'Hospital'a ma charakter uniwersalny także w tym sensie że może być pośrednio zastosowane także w odniesieniu do innych podstawowych wyrażeń nieoznaczonych po odpowiednich ich przekształceniu.

20. Badanie przebiegu zmienności funkcji jednej zmiennej (omówienie).

I ETAP: podstawowe informacje

1. Dziedzina funkcji

a)iloraz: wykluczamy z dziedziny miejsca zerowe mianownika

b)pierwiastek parzystego stopnia: wyrażenie pierwiastkowane musi być nieujemne.

c)logarytm: wyrażenie logarytmowane musi być dodatnie.

2. Miejsca zerowe funkcji f(x) = 0 ⇒ miejsca zerowe funkcji są punktami przecięcia lub styczności z osią OX

3. punkty przecięcia z osią OY:f(0)- (o ile istnieją)

II ETAP: asymptoty wykresu funkcji

1. asymptoty pionowe: obliczamy granica jednostronne w punktach nieciągłości oraz na skończonych krańcach dziedziny. Jeżeli przynajmniej jedna z granic jednostronnych jest niewłaściwa to w punkcie występuje asymptota pionowa(lewostronna, prawostronna lub obustronna)

2. asymptoty poziome

3. asymptoty ukośne

m = lim
k = lim [f(x) - mx]

x→(±)∞ x→(±)∞

Jeżeli obie te granice są właściwe(skończone) to prosta o równaniu y =mx +k jest asymptotą poziomą(m=0) lub ukośną (m≠ 0 )prawostronna (tzn w + ∞ )lub lewostronna( w - ∞).

III ETAP: analiza pochodnych

1. przedziały monotoniczności

f `(x) > 0 ⇒ funkcja rosnąca

f `(x) < 0 ⇒ funkcja malejąca

2. ekstremum lokalne

a)warunek konieczny: f `(x) = 0 => kandydat na ekstremum lokalne

b)warunek dostateczny: zmiana znaku pochodnej w sąsiedztwie kandydata

3. wklęsłość, wypukłość i punkty przegięcia

f ”(x) > 0 ⇒ funkcja wypukła

f ”(x) < 0 ⇒ funkcja wklęsła

Dla punktu przegięcia:

a)warunek konieczny: f ”(x) = 0 => kandydat na punkt przegięcia,

b)warunek dostateczny: zmiana znaku drugiej pochodnej w sąsiedztwie kandydata

21. Asymptoty wykresu funkcji.

1. Asymptoty pionowe:

Zakładamy że funkcja f(x) jest określona w pewnym sąsiedztwie punktu x₀

Prostą o równaniu x = x₀ nazywamy asymptotą pionową wykresu funkcji y = f(x) ⇔ gdy przynajmniej jedna z granic jednostronnych funkcji f(x) w punkcie x₀ jest niewłaściwa.

Mówimy wówczas odpowiednio o asymptocie lewostronnej, prawostronnej lub obustronnej. WNIOSKI: Jeżeli przynajmniej jedna z tych granic jednostronnych jest niewłaściwa to w danym punkcie występuje asymptota pionowa (lewo, prawo lub obustronnie)

W punkcie „a” występuje prawostronna as. Pionowa, a w punkcie” x₀” obustronna as. pionowa.

2. Asymptoty poziome, ukośne

y=mx+k

Zakładamy że funkcja f(x) jest określona w pewnym prawostronnym lub lewostronnym nieograniczonym przedziale. Mówimy, że prosta o równaniu y=mx+k(postać kierunkowa) jest as. poziomą lub ukośną wykresu funkcji f(x) <=>,gdy:

lim [f(x) - mx] = 0

x→(±)∞

To znaczy: różnica pomiędzy wartością na krzywej y = f(x) i na prostej y =mx + k zmierza do zera, gdy x→ +∞ (lub gdy x→ -∞)

lim [f(x) - mx] = m - współczynnik kierunkowy asymptoty

x→(±)∞

Dla danego m wyznaczonego z powyższego wzoru możemy z definicji asymptoty wyznaczyć współczynnik k.

lim [f(x) - mx] = k

x→(±)∞

PRAKTYCZNIE: Jeżeli obie powyższe granice są właściwe to wówczas prosta o równaniu y=mx+k jest asymptotą poziomą(gdy m=0) lub ukośną gdy (m≠ 0) prawostronna (tzn gdy x→ +∞) lub lewostronna (tzn. x→ -∞).

y=k2-lewostronn as. pozioma(tzn. x→ -∞).

y=m1+k1-prawostronna as ukośna(tzn gdy x→ +∞)

22. Ekstremum lokalne funkcji jednej zmiennej.

Niech f(x) będzie funkcją określoną w pewnym otoczeniu punktu x₀.

Mówimy, że funkcja f(x) osiąga ekstremum lokalne w punkcie x₀ <=>, gdy wartość funkcji w punkcie x₀ jest lokalnie największa lub najmniejsza. To znaczy: w porównaniu z wartościami funkcji w pewnym sąsiedztwie tego punktu.

1. ٧ ٨ f(x) < f(x₀) maksimum lokalne w punkcie x₀

δ>0 x∈S(x₀,δ)

2. ٧ ٨ f(x) > f(x₀) - minimum lokalne w punkcie x₀

δ>0 x∈S(x₀, δ)

Przyjmując dodatkowo założenie o różniczkowalności funkcji f(x) w punkcie x₀, możemy opisać warunek konieczny i dostateczny istnienia ekstremum lokalnego w punkcie x_0.

1. warunek konieczny istnienia ekstremum lokalnego funkcji f(x) w punkcie x₀ (dla f. różniczkowalnej)Jeżeli w punkcie x₀ funkcja f(x) osiąga ekstremum lokalane to f `(x₀) = 0.

Twierdzenie odwrotne nie jest prawdziwe, to znaczy : Jeżeli f `(x₀) = 0 to nie wystarczy do stwierdzenia, że w punkcie x₀ występuje ekstremum lokalne(bo może być p.p).

2. warunek dostateczny(wystarczający) istnienia ekstremum lokalnego funkcji f(x), w którym spełniony jest warunek konieczny(kandydat na e.l.). Jeżeli w sąsiedztwie kandydata pochodna zmienia znak to w danym punkcie funkcja osiąga e.l, przy czym:

*jeżeli w sąsiedztwie kandydata (spełniającego warunek konieczny)pochodna zmienia znak z +(f.rosnąca) na -(f.malejąca) to w danym punkcie funkcja osiąga maksimum lokalne.

*Jeżeli w sąsiedztwie kandydata pochodna zmienia znak z - na + to w danym punkcie występuje minimum lokalne

*jeżeli a sąsiedztwie kandydata pochodna nie zmienia znaku to brak ekstremum lokalnego w danym punkcie (punkt przegięcia)

PRAKTYCZNIE:

ad.a) warunek konieczny: f `(x) = 0 miejsca zerowe pochodnej są kandydatami na ekstremum lokalne

ad.b)warunek dostateczny: zmiana znaku pochodnej w sąsiedztwie kandydata

Warunek dostateczny dotyczący ekstremum lokalnego w punkcie, w którym występuje ostrze jest identyczny jak dla funkcji różniczkowalnej w danym punkcie, tzn. zmiana znaku pochodnej w sąsiedztwie kandydata.

Dla punktów, w którym występuje ostrze jako kandydat na e.l. warunek dostateczny musi być odpowiednio spełniony.

23. Wklęsłość i wypukłość wykresu funkcji. Punkty przegięcia.

Zakładamy, że funkcja f(x) jest ciągła w przedziale (a,b).

1)Mówimy, że krzywa (wykres funkcji) jest wklęsła w przedziale (a,b) <=>, gdy krzywa ta jest położona poniżej stycznej poprowadzonej do wykresu funkcji w dowolnym punkcie wewnętrznym tego przedziału.

2)Mówimy o krzywej wypukłej w przedziale (a,b) <=>, gdy krzywa jest położona powyżej stycznej poprowadzonej do wykresu funkcji w danym przedziale.

3)Mówimy, że x₀ jest punktem przegięcia wykresu funkcji f(x) <=>, gdy w sąsiedztwie tego punktu krzywa przechodzi z wklęsłej w wypukłą lub odwrotnie.

Badanie wklęsłości, wypukłości i punktu przegięcia jest oparte na analizie drugiej pochodnej f. przy czym przez drugą pochodną funkcji f(x) rozumiemy pochodną pierwszej pochodnej i piszemy f ``(x)= [f `(x)]`

Zakładamy, że funkcja f(x) jest dwukrotnie różniczkowalna w przedziale (a,b), to znaczy istnieje pierwsza i druga pochodna w każdym punkcie wewnętrznym danego przedziału.

ad.1) ٨ f ``(x)<0 => krzywa(funkcja) jest wklęsła w przedziale (a,b)

x∈(a,b)

ad.2) ٨ f ``(x) >0 => krzywa jest wypukła w przedziale (a,b)

x∈(a,b)

ad.3) a) warunek konieczny dla punktu przegięcia: Jeżeli x₀ jest punktem przegięcia wykresu funkcji f(x) to f ``( x₀)=0. Inaczej mówiąc: Zerowanie się drugiej pochodnej jest warunkiem koniecznym istnienia punktu przegięcia, ale nie jest warunkiem wystarczającym (dostatecznym). To znaczy: twierdzenie odwrotne nie jest prawdziwe.

PRAKTYCZNIE : f ``(x)=0 => miejsca zerowe drugiej pochodnej są kandydatami na p.p.

b)warunek dostateczny dla punktu spełniającego warunek konieczny(kandydat na p.p.):

Zmiana znaku drugiej pochodnej w sąsiedztwie kandydata. UWAGA! Odrzucony kandydat na ekstremum lokalne jest punktem przegięcia i odwrotnie, to znaczy: odrzucony kandydat p.p. jest ekstremum lokalnym danej funkcji, dotyczy to f. różniczkowalnej.

Innym kandydatem na punkt przegięcia jest punkt, w którym występuje tak zwane ostrze, to znaczy funkcja jest ciągła, ale nie jest różniczkowalna w tym punkcie (brak pochodnej).

Kandydat na ekstremum lokalne i punkt przegięcia jako ostrze może być jednocześnie ekstremum lokalnym i p.p. lub odrzuconym kandydatem w obu przypadkach (inaczej niż dla funkcji różniczkowalnej).

24. Całka nieoznaczona - definicja i podstawowe własności.

Przez całkowanie funkcji jednej zmiennej rozumiemy tzw. wyznaczanie funkcji pierwotnej F(x), tzn. takiej funkcji, której pochodna jest równa funkcji całkowanej, przy czym F(x) jest f. pierwotną dla funkcji f(x) to wówczas

[F(x)+C]`=F`(x)+C`=f(x), gdzie C=const.(dowolna stała)

Oznacza to, że: w wyniku całkowania (całkom nieoznaczonym) trzymujemy nieskończenie wiele tkz. krzywych całkowych różniących się o pewną stałą.

SYMBOLICZNIE:

∫ f(x) dx = F(x) +C ⇔(def) F `(x) = f(x), gdzie :

f(x)-funkcja całkowana

dx- różniczka zmiennej całkowania (różniczka zmiennej niezależnej x)

f(x)*x-wyrażenie podcałkowe

F(x)- funkcja pierwotna (całka nieoznaczona), tzn F`(x)=f(x)

C=const.(dowolna stała)

Podstawowe własności całki nieoznaczonej.

1. ∫ [f(x) + g(x)] dx = ∫ f(x) dx + ∫ g(x) dx = F(x) + G(x) + C, gdzie:

F(x) iG(x) są funkcjami pierwotnymi odpowiednio dla funkcji całkowanych f(x) i g(x).

2. ∫ [f(x) - g(x)] dx = ∫ f(x) dx - ∫ g(x) dx

3. ٨ ∫ [α*f(x)] dx = α*∫ f(x) dx = α* f(x) dx

α∈R

4. Całkowanie przez podstawianie

∫f(x) dx = ∫f [ϕ(t)] * ϕ'(t)dt,

x=ϕ(t)=>dx=ϕ`(t)*dt

5. Całkowanie przez części: Przekształcając wzór na pochodną iloczynu dwóch funkcji otrzymamy:

[u(x) * v(x)]`=u`(x)*v(x)+u(x)*v`(x)

u`(x)*v(x)=[u(x)*v(x)]`- u(x)*v`(x) /*dt/ ∫ ( )

Mnożąc przez różniczkę dx i całkując obustronnie otrzymamy ostatecznie:

∫ [u'(x)*v(x)] dx = u(x)v(x) - ∫ [u(x)v'(x)] dx.

25. Zestawienie podstawowych całek.

1. funkcja potęgowa:

∫x^a dx =
+ C, dla a ≠ -1

ln|x|+C, dla a = -1

UZASADNIENIE:

a)dla a ≠-1 =>
=(a+1)*x/(a+1)=x^a

b) dla a = -1=>

(i) x>0 =>(lnx)`=1/x

(ii)x<0 =>([n(-x)]`=1/-x*(-1)=1/x

2. funkcja wykładnicza: ∫a^x dx =
+ C

w szczególności: ∫e^x dx = e^x + C

3. funkcje trygonometryczne:

a) ∫ sin x dx = - cos x + C

b) ∫ cos x dx = sin x + C

c) ∫ tg x dx = - lncos x+ C

d) ∫ ctg x dx = lnsin x+ C

e) ∫
= tgx + C

f) ∫
= - ctgx +b C

g) ∫(1 + tg²x) dx = tgx + C

h) ∫(1 + ctg²x) dx + C

4. funkcje cyklometryczne:

a) ∫ arcsin x dx = x*arcsin x +
+ C

b) ∫ arccos x dx =x*arccos x -
+ C

c) ∫ arctg x dx = x* arctg x - ½ ln1 + x² + C

d) ∫ arcctg x dx = x* arcctg x + ½ ln1 + x² + C

26. Całkowanie funkcji wymiernych.

f(x)=Pn(x)/Qm(x) Funkcja wymierna jako iloraz wielomianów odpowiednio stopnia n i m

ETAP I: n
m => dzieląc licznik przez mianownik (dzielenie wielomianów otrzymamy:

, gdzie k<m

Wielomian stopnia (n-m) całkujemy bezpośrednio.

ETAP II: Całkowanie funkcji wymiernej

Pn(x)/Qm(x), gdzie k<m, polega na rozkładzie tej funkcji na sumę tkz. ułamków prostych.

1)
- ułamek prosty pierwszego rodzaju, gdzie:

A=const. (trzeba wyznaczyć)

x₀-miejsce zerowe mianownika [Qm(x)]

i-krotność miejsca zerowego x₀ (i∈N)

2)
-ułamek prosty drugiego stopnia, gdzie

B,C-= const. (trzeba wyznaczyć)

x^2+px+q-nierozkładalny trójmian kwadratowy,
, wystepuje w rozkładzie mianownika[Qm(x)] na czynniki (trójmian ten odpowiada urojonym miejsca zerowym mianownika)

j- krotność trójmianu nierozkładalnego w rozkładzie mianownika na czynniki j∈N

ETAP III: Całkowanie ułamków prostych:

1)

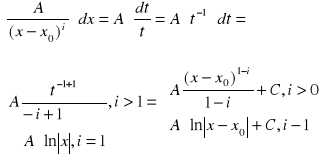
2) ∫
*dx - Całkowanie ułamka prostego drugiego rodzaju, dla j=1(pozostałe przypadki pomijamy)realizujemy w dwóch etapach-krokach

KROK I

∫
*dx=B/2*2x+p/x^2+px+q*dx+∫C-
/ x^2+px+q*dx=B/2*ln|x^2+px+q|+(C+B/2)* ∫dx/x^2+px+q

KROK II: Funkcje całkowaną

, gdzie
sprowadzamy prze odpowiednie podstawianie do postaci pochodnej funkcji arctgt, tzn 1/1+t^2 bo wówczas:

∫dt/1+t^2=arctgt+C

27. Własności całek oznaczonych i podstawowe interpretacje.

1) Formalnie całka oznaczona Reimanna w przedziale całkowania [a,b] jest zdefiniowana jako właściwa granica ciągu sum całkowych Riemanna pry założeniu, że ciąg podziałów przedziału całkowania [a,b] jest normalny (norma podziałów dąży do zera).

Praktycznie: Obliczając całkę oznaczoną funkcji f(x) w przedziale [a,b] będziemy wykorzystywać mówiące o związku całki oznaczonej z całką nieoznaczoną(funkcją pierwotną).

Twierdzenie Leibniz'a - Newton'a

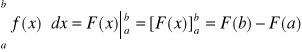
Oznacza to, że: Całka oznaczona funkcji f(x) w przedziale [a,b] jest równa różnicy wartości funkcji pierwotnej F(x) w górnej i dolnej granicy całkowania.

2) Elementarne własności związane z granicami całkowania:

a)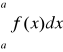
= 0

b)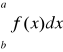
= -

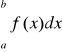
c) dla każdego c ∈ (a; b)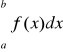
=
+

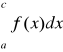
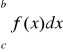
3) Podstawowe interpretacje geometryczne:

a)

[dla każdego x∈[a,b] f(x)
0] =>[Pd =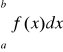
]

Oznacza to, że: Jeżeli funkcja f(x) przyjmuje nieujemną wartość w przedziale [a; b], to pole obszaru D zawartego pomiędzy wykresem funkcji y=f(x) i osią OX w zakresie przedziału [a,b] jest opisane całką oznaczoną funkcji f(x) w przedziale [a,b].

b)

[dla każdego x∈[a,b] f(x)
0] =>[Pd= -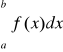
]

To znaczy: Jeżeli w przedziale [a,b] funkcja przyjmuje niedodatnie wartości to pole obszaru zawartego pomiędzy krzywą y=f(x) i osią OX opisuje wartość przeciwna całki oznaczonej funkcji f(x) w przedziale [a,b].

c)

[dla każdego x∈[a,b] f(x)
g(x)] =>[Pd =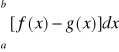
]

To znaczy: Jeżeli obszar D jest ograniczony z góry przez krzywą y=f(x), a z dołu przez krzywą y=g(x) to pole obszaru D zawartego pomiędy tymi krzywymi jest opisane całką oznaczoną różnicy [f(x)-g(x)] w przedziale [a,b] przy czym „a” i ”b” są odpowiednimi odciętymu punktów przecięcia danej krzywej.

28. Całki niewłaściwe.

Całkowalność funkcji w sensie Riemanna (całka oznaczona wymaga zarówno ograniczoności przedziału całkowania [a,b] jak i ograniczoności funkcji całkowanej w przedziale całkowanym. Jeżeli przynajmniej jeden warunek nie jest spełniony to mówimy o całkach niewłaściwych.

Ze wzgl. na niespełnienie warunku ograniczoności funkcji w przedziale całkowania wyróżnia się dwa rodzaje całek niewłaściwych:

1.ze wzgl. na nieograniczony przedział całkowania

2.ze wzgl. na nieograniczoność funkcji w przedziale całkowania

ad.1

a)jeżeli funkcja f(x) jest określona (i całkowana) w prawostronnym nieograniczonym przedziale <a,+∞) to wówczas całkę oznaczoną funkcji f(x) rozumiemy jako granicę całki w przedziale <a,b>, gdy prawy kraniec przedziału dąży do +∞, tzn.

Mówimy że całka niewłaściwa w przedziale <a,+∞) jest granicą całki oznaczonej w przedziale <a,b>, gdy b→+∞ .

b)Całka niewłaściwa w przedziale (-∞,b>(lewostronnie nieograniczonym), wówczas:

W przedziale (-∞ .,b] jesr granicą całki oznaczonej w przedziale [a,b], gdy a→-∞ .

c) Całka niewłaściwa w przedziale (-∞,+∞) (obustronnie nieograniczonym)

gdzie c∈R

UWAGA! Jeżeli odpowiednia granica całki oznaczonej jest właściwa (skończona) to mówimy, że dana całka niewłaściwa jest zbieżna.

Ad.2

Całki niewłaściwe II rodzaju ze wzgl. na nieograniczoność funkcji w przedziale całkowania

1. nieograniczoność całki w punkcie „a” (prawostronna asymptota w tym punkcie)

Oznacza to, że całka niewłaściwa w przedziale [a,b](ze względu na nieograniczoność w punkcie „a” jest granicą całki oznaczonej w przedziale (a+
;b], gdy
→

W sensie geometrycznym, gdy w przedziale całkowania f(x)
0 to całka niewłaściwa w przypadku a) opisuje pole obszaru PD zawartego pomiędzy krzywą i osią OX.

b)Nieograniczoność w punkcie „b” (lewostronna as. pionowa w tym punkcie)

Całka niewłaściwa w przedziale [a,b] (z nieograniczonością w punkcie b jest granicą oznaczonej w przedziale [a,-b-
] gdy
→
, przy czym pole D opisuje wartość przeciwna tej całki niewłaściwej.

c)Nieograniczoność funkcji całkowanej punkcie wewnętrznym c
(a,b)(as. pionowa w punkcie c, przynajmniej jednostronna).

Jeżeli odpowiednie granice całek oznaczonych są właściwe(skończone) to mówimy, że dana całka niewłaściwa jest zbieżna.

31. Przestrzeń wektorowa - podstawowe pojęcia.

Wektorem
nazywać będziemy n-kę uporządkowaną liczb rzeczywistych
= [x₁, x₂, .., x_n], gdzie liczby rzeczywiste x₁, x₂, .., x_n ∈ R, nazywamy składowymi wektora
.

W zastosowaniach najczęściej wektor o n składowych opisuje stan pewnego obiektu (człowieka, firmy, gospodarki itp.)

Przestrzenią wektorową n-wymiarową Rⁿ rozpiętą nad ciałem liczb rzeczywistych, nazywamy zbiór wszystkich wektorów o n-składowych, w którym określone są następujące działania:

1. Dodawanie wektorów - sumą wektorów przestrzeni Rⁿ jest wektor s składowych, które są sumami kolejnych składowych wektorów
i
.

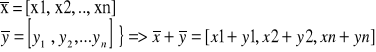
2. Mnożenie wektora przez liczbę α ∈ Rⁿ. α _*
= [αx_1; α x_{2; ...;}α x_n] ∈ Rⁿ.

Kolejne składowe wektora mnożymy przez daną liczbę.

INACZEJ mówiąc: Przestrzeń wektorowa Rⁿ jest to zbiór wektorów o n składowych, który jest zamknięty ze względy na dodawanie wektorów i mnożenie wektora przez liczbę (tkz. wyniki tych działań są także wektorami tej samej przestrzeni Rⁿ.

3. Specyficznym działaniem na wektorach w przestrzeni Rⁿ jest iloczyn skalarny wektorów, którego wynik jest liczbą (skalarem), a nie wektorem.

°
= x_{1 *} y₁ + x_{2 *} y₂ + .._⋅ + x_{n *} y_n =
∈ R

To znaczy: iloczyn skalarny wektorów jest równy sumie iloczynów kolejnych składowych obu wektorów.

Kombinacją liniową wektorów
;
; ... ;
∈ Rⁿ nazywamy wektor postaci
= α₁
+ α₂
+ ... + α_k
∈ Rⁿ , gdzie liczby rzeczywiste α_1, α_{2, ...,} α_k∈ R są współczynnikami tej kombinacji liniowej.

Przestrzeń wektorowa jest przestrzenią Rⁿ liniową w tym sensie, że kombinacja liniowa dwóch dowolnych wektorów przestrzeni Rⁿ jest także wektorem tej przestrzeni, tzn

Dla każdego(
,
∈ Rⁿ )α₁
+ α₂
∈ Rⁿ

Bazą przestrzeni wektorowej Rⁿ nazywamy każdy najmniejszy układ wektorów generujący tę przestrzeń.

Inaczej mówiąc: Każdy wektor przestrzeni Rⁿ można przedstawić w postaci kombinacji liniowej bazy(układ generujący).

32. Liniowa zależność i niezależność wektorów.

1.Mówimy że układ wektorów
;
; ... ;
w przestrzeni Rⁿ jest liniowo niezależny ⇔ gdy α₁
+ α₂
+ ... + α_k
=
⇔ α_{1 =} α_{2 = ... =} α_k = 0 , gdzie
= [0; 0; ...; 0] ∈ Rⁿ jest tzw. wektorem zerowym przestrzeni Rⁿ.

Oznacza to,że kombinacja liniowa wektorów liniowo niezależnych jest równa zerowemu <=>,gdy wszystkie współczynniki tej kombinacji są (muszą być) równe zero.

Inaczej mówiąc: Aby w kombinacji liniowej wektorów liniowo niezależnych uzyskać wektor zerowy trzeba przyjąć wszystkie współczynniki tej kombinacji równe zero (trywialna kombinacja liniowa).

2. Mówimy że układ wektorów jest liniowo zależny ⇔ gdy nie jest to układ liniowo niezależny (def. komplementarna). Inaczej mówiąc aby w kombinacji liniowej wektorów liniowo zależnych otrzymać wektor zerowy, nie wszystkie współczynniki tej kombinacji muszą być równe zero (przynajmniej jeden ze współczynników może być równy zero).

Inaczej mówiąc: Dla wektorów liniowo zależnych istnieje nietrywialna kombinacja liniowa (nie wszystkie współczynniki są zerami, która daje wektor zerowy).

33. Definicja i rodzaje macierzy

Macierzą o wymiarach (m×n) nazywamy odwzorowanie iloczynu kartezjańskiego dwóch podzbiorów zbioru liczb naturalnych N₁×N₂, gdzie N₁ = {1; 2; ...; m} ; N₂ = {1; 2; ...; n} w zbiór R.

M=( N₁×N₂ )→R

Oznacza to że macierz o wymiarach (m×n) jest odwzorowaniem, którego dziedziną jest iloczyn kartezjański N₁×N₂ tzn. zbiór uporządkowanych par liczb naturalnych (i, j), takich że i∈N_{1 ;} j∈N₂, a przeciw dziedziną jest pewien podzbiór zawarty w zbiorze R, czyli wartościami tego odwzorowania są liczby rzeczywiste a_ij, przyporządkowane parom indeksów i, j.

Praktycznie: Macierz o wymiarach (mxn) przedstawiamy w postacie prostokątnej tablicy liczb (elementów macierzy) o m wierszach (poziomo) oraz n kolumnach (pionowo)

Macierz o elementach aij, o wymiarach (mxn), gdzie:

m-liczba wierszy(pierwszy wymiar macierzy)

n-liczba kolumn(drugi wymiar macierzy)

i-numer wiersza(pierwszy indeks)

j-numer kolumn(drugi ineks)

aij-element występujący na przecięciu i-tego wiersza oraz j-tej kolumny.

Podstawowe rodzaje macierzy

1. Macierz A=[aij]
nazywamy macierzą kwadratową <=>, gdy m=n

Z macierzą kwadratową związane są dwa pojęcia:

a)przekątną główną macierzy kwadratowej stanowią elementy opisane parą równych indeksów

b)o macierzy kwadratowejo wymiarach mxn mówimy krótko: macierz stopnia n

2.Macierz kwadratową A=[aij]
(stopnia n) nazywamy macierzą trójkątną <=>, gdy wszystkie elementy położone powyżej głównej przekątnej lub poniżej głównej przekątnej są równe zero, tzn.

Macierz trójkątna dolna, tzn wszystkie elementy powyżej głównej przekątnej są zerami, czyli dla każdego i<j aij=0

Macierz trójkątną górną same zera poniżej głównej przekątnej, czyli, dla każdego i>j aij=0

3. Jeżeli w macierzy kwadratowej wszystkie elementy poza główną przekątną są równe zero, to mówimy o macierzy diagonalnej.

Macierz diagonalna (przekątniowa), dla każdego i
j aij=0

4. Jeżeli w macierzy diagonalnej dodatkowo wszystkie elementy głównej przekątnej są równe jeden, to mówimy o macierzy jednostkowej.

Macierz jednostkowa stopnia n

5. Macierz o wymiarach (m×n) (niekoniecznie kwadratowa) jest macierzą zerową ⇔ gdy wszystkie elementy tej macierzy są równe.

34. Działania na macierzach i ich własności.

1. Dodawanie macierzy

A = [a_ij] _m×n ; B = [b_ij] _m×n

Sumą macierzy A i B nazywamy macierz C = A + B = [c_ij]_m×n, gdzie

٨ c_{ij =} a_{ij +} b_ij

i=1,2,..,m

j=1,2,...,n

Warunek istnienia sumy dwóch macierzy jest identyczność ich wymiarów (mxn)

2. Transpozycja macierzy - macierz transponowana powstaje z macierzy A = [a_ij] _m×n przez zamianę wierszy z kolumnami z zachowaniem ich kolejności

A^T = [a_ji]_n×m- -macierz transponowana(przestawiamy)

3. Mnożenie macierzy przez liczbę rzeczywistą α∈R - mnożymy wszystkie elementy danej macierzy przez liczbę α.

α _* A = [α _* a_ij] _m×n

4. Mnożenie macierzy przez macierz - polega na mnożeniu wierszy pierwszej macierzy przez kolumny drugiej macierzy w sensie iloczynu skalarnego wektorów. Warunkiem istnienia iloczynu dwóch macierzy jest równość kolumn pierwszej macierzy i liczby wierszy drugiej macierzy.

Niech A=[aij]
, B=[bij]
-wprowadzamy następujące oznaczenia wektorowe

i-ty wiersz macierzy A jako wierszowy wektor przestrzeni R^k

j-ta kolumna macierzy B jako kolumnowy wektor przestrzeni R^k

Iloczynem macierzy A i B nazywamy macierz C=A*B=[cij]mxn <=> dla każdego (i=1,2…m; j=1,2…n)
-(iloczyn skalarny wektorów).

Warunkiem istnienia iloczynu dwóch macierzy jest równość liczby kolumn pierwszej macierzy i liczby wierszy drugiej macierzy.

W wyniku mnożenia dwóch macierzy otrzymujemy macierz o wymiarach (mxn), gdzie m jest m jest liczbę wierszy pierwszej macierzy,a n jest liczbą kolmun drugiej macierzy.

Własności działań na macierzach:

1. Przemienność:

*A + B = B + A

*α × A = A × α

*A × B = B × A - (przekreślić)-zasada nie przemienności mnożenia macierzy(istnieją wyjątki)

2. Łączność

*A + (B + C) = (A + B) + C

*(α × B) × A = α × (B × A)

*A × (B × C) = (A × B) × C

3. Rozdzielność

*α × (A + B) = (α × A) + (α × B)

*(α + β) × A = (α × A) + (β × A)

*A × (B + C) = A × B + A × C

*(A + B) × C = (A × C) + (B × C)

*(A + B)^T = A^T + B^T

*(α × A)^T = α × A^T

*(A × B)^T = B^T × A^T

4. Podwójna transpozycja: (A^T )^T = A

5. Mnożenie przez macierz jednostkową

*A _m×n × I_n = A _m×n

*I_m × A _m×n = A _m×n

*A_n×n × I_n = I_n × A_n×n = A_n×n

Pierwszy wyjątek od zasady nie przemienności mnożenia macierzy, to znaczy mnożenie macierzy kwadratowej przez macierz jednostkową tego samego stopnia jest przemienne.

35. Definicja wyznacznika macierzy.

Wyznacznik macierzy jest to odwzorowanie, które każdej macierzy kwadratowej przyporządkowuje dokładnie jedną liczbę rzeczywistą.

Inaczej mówiąc: Każdej macierzy kwadratowej przyporządkowane jest dokładnie jedna liczba rzeczywista zwana wyznacznikiem tej macierzy.

Sekwencyjna i rekurencyjna definicja wyznacznika:

Sekwencja definicji wyznacznika oznacza, że opisujemy sposób obliczania wyznacznika dla macierzy kwadratowej kolejnych stopni. OZNACZENIA: det.-determinant=wyznacznik

1. n = 1 ⇒ A = [a₁₁] ⇒ detA = a₁₁

2. n = 2 ⇒ detA = 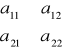
 = a₁₁× a₂₂ - a₁₂ × a₂₁

3. n = 3 ⇒ SCHEMAT SARRUSA

detA =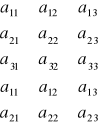
= S₁ - S₂

Zgodnie ze schematem Sarrusa wyznacznik tzreciego stopnia jest równy różnicy dwóch sum S₁ - S₂ przy czym S₁ jest sumą trzech iloczynów po trzey elementy na głównej przekątnej i równolegle do niej, sama S₂ powstaje analogicznie poczynając od drugiej przekątnej.

4. n ≥ 4 ⇒ rozwinięcie LAPLACE'a

Wprowadzamy dwa nowe pojęcia:

*M_ij - minor, tzn. podwyznacznik stopnia (n-1), powstający przez wykreślenie i-tego wiersza i j-tej kolumny,

*D_ij = (-1) ^i+j × M_ij - dopełnienie algebraiczne elementu a_ij macierzy A = [a_ij]_n×n , to znaczy minor z odpowiednim znakiem

(-1) ^i+j = (klamra)( +1 dla (i+j)parzystego),( -1 dla (i+j) nieparzystego)

Zgodnie z rozwinięciem LAPLACE'a wyznacznik stopni wyższych (n≥ 4) można przedstawić w postaci sumy iloczynów wybranego wiersza lub kolumny oraz odpowiadających im dopełnień algebraicznych.

detA =
- rozwinięcie wyznacznika względem i-tego wiersza

detA =
- rozwinięcie wyznacznika względem j-tej kolumny

UWAGI: *Bez względu na wybór wiersza lub kolumny do rozwinięcia danego wyznacznika wyższego stopnia wynik to znaczy detA musi być ten sam(jednoznaczność)

*Rekurencyjność powyższej definicji wyznacznika stopni (n≥ 4) są opisane przez wyznaczniki niższych stopni tio znaczy minory w rozwinięciu Laplace'a.

36. Własności wyznacznika macierzy.

1. Wyznacznik macierzy jest równy zero jeżeli:

* macierz zawiera wektor równy zerowy(wiersz lub kolumna zawierająca same zera)

*macierz zawiera wektory współliniowe(kolinearne tzn. jeden z wektorów jest iloczynem innego z wektorów i pewnej liczby rzeczywistej).

2. Wyznacznik macierzy trójkątnej także diagonalnej jest równy iloczynowi elementów głównej przekątnej, tzn detA=a11*a22*….*ann. W SZCZEGÓLNOŚCI: dla macierzy jednostkowej dowolnego stopnia mamy:

Dla każdego n∈N det(In)=1

3. Mówimy o macierzy osobliwej <=>, gdy jest to macierz kwadratowa o wyznaczniku równym zero.

Mówimy że macierz jest nieosobliwa ⇔ gdy jest to macierz kwadratowa o wyznaczniku różnym od zera.

* detA=0 <=> macierz A jest osobliwa

*det A
0 <=> macierz A jest nieosobliwa

4. Wyznacznik sumy dwóch macierzy na ogół nie jest równością prawdziwą.

det(A + B) ≠ detA + debt (przekreślić)

5. det(A^T) = detA -transpozycja nie zmienia wyznacznika macierzy

6.det(A × B) = detA × detB - pod warunkiem że są to macierze kwadratowe tego samego stopnia.

7.Suma iloczynów elementów wybranego wiersza oraz dopełnień algebraicznych elementów innego wiersza dnaej macierzy kwadratowej jest równa zero.

=(klamra) [0, gdy i≠k (różne wiersze)], [detA, gdy i=k (rozwinięcie Laplace'a]

Analogiczną własność można sformułować dla kolu,Mn macierzy kwadratowej.

8. Przekształcenia elementarne macierzy(operacje elementarne):

I. Pierwsze przekształcenie elementarne polega na przestawieniu ze sobą dwóch wektorów w danej macierzy. Wówczas wartość wyznacznika zmienia się na przeciwną.

II. Drugie przekształcenie elementarne polega na pomnożeniu jednego z wektorów danej macierzy przez liczbę α ∈ R. Wówczas wyznacznik takiej macierzy będzie równy α × detA Natomiast jeżeli pomnożymy macierz A przez liczbę α to wówczas det(α × A) = αⁿ × detA, gdzie n jest stopniem macierzy kwadratowej A

III. Trzecie przekształcenie elementarne polega na dodaniu do jednego z wektorów danej macierzy kombinacji liniowej pozostałych wektorów tej macierzy. Wówczas wartość wyznacznika nie zmienia się.

Inaczej mówiąc wyznacznik nie zmienia wartości jeżeli do jednego z wierszy dodamy kombinacje liniową (o dowolnych współczynnikach)pozostałych wierszy tej macierzy(analogicznie dla kolumn).

37. Macierz odwrotna i jej własności.

Macierz A^-1 nazywamy macierzą odwrotną do macierzy A ⇔ gdy A × A^-1 = A^-1 × A = I.

To znaczy iloczyn macierzy podstawowej a i odwrotnej A^-1 jest równy macierzy jednostkowej.

KOMENTARZE:

1. Oznaczenie A^-1 jest symbolem macierzy odwrotnej, a nie odwrotnością macierzy. A^-1 =1/A(przekreślone)

2. Definicja macierzy odwrotnej zawiera drugi wyjątek od zasady nie przemienności mnożenia macierzy, to znaczy mnożenie macierzy podstawowej A przez macierz odwrotna A^-1 jest przemienna.

3. Wymiana macierzy

Oznacza to, że: Definicja macierzy odwrotnej wymaga aby macierz podstawowa A była kwadratowa(m=n), a wówczas macierz odwrotna jest także kwadratowa(k=l) tego samego stopnia.

4. Wyznacznik macierzy

(A^-1× A=I)=>det(A^-1× A)=det(I)<=>det(A^-1)=1<=>det(A^-1)=1/detA

Oznacza to, że macierz podstawowa A musi być nieosobliwa [detA ≠ 0]. Wówczas macierz odwrotna jest także nieosobliwa, przy czym wyznacznik macierzy odwrotnej jest równy odwrotności wyznacznika macierzy podstawowej.

5. Macierz odwrotna A^-1istanieje <=>, gdy macierz podstawowa A jest kwadratowa i nieosobliwa detA≠ 0

Własności macierzy odwrotnej:

1) (A + B)^-1 = A^-1 + B^-1(przekreślić) Macierz odwrotna dla sumy dwóch macierzy nie jest równa sumie macierzy odwrotnych.

2) (α × A)^-1 =
× A^-1, gdzie: α≠0

3) (A^T)^-1 = (A^-1)^T

To znaczy: Macierz odwrotna do macierzy transponowanej jest równa transponowanej macierzy odwrotnej.

2. (A × B)^-1 = B^-1 × A^-1 ! Macierz odwrotna do iloczynu dwóch macierzy (nieosobliwych tego samego stopnia) jest równa macierzy odwrotnych za zmianą kolejności.

UZASADNIENIE: (A × B) ×( B^-1 × A^-1)=A×(B× B^-1) × A^-1=(A×I) × A^-1=A× A^-1=I

3. det(A^-1) = 1/detA Wyznacznik macierzy odwrotnej jest równy odwrotności wyznacznika macierzy podstawowej (detA≠0)

38. Rząd macierzy i jego własności.

Rzędem macierzy A = [a_ij] _m×n (niekoniecznie kwadratowej) nazywamy liczbę liniowo niezależnych wektorów tej macierzy.

Rząd macierzy jest równy zero ⇔ gdy macierz jest macierzą zerową, tzn. wszystkie wektory tej macierzy są wektorami zerowymi, a więc liniowo zależnymi.

OZNACZENIE: rzA=r(A)=R(A) (przekreślone)

Własności rzędu macierzy:

1. Rząd macierzy nie może być większy niż mniejszy z wymiarów tej macierzy: rz(A _m×n) ≤ {m; n}

2. Rząd macierzy diagonalnej jest równy liczbie niezerowych elementów głównej przekątnej.

3. Rząd macierzy nieosobliwej jest równy jej stopniowi. [detA(A _m×n) ≠0]=>[rz(A _m×n)=n]

Wówczas zarówno wiersze jak i kolumny macierzy nieosobliwej stanowią bazę przestrzeni Rⁿ, jako układy zawierające dokładnie n-liniowo niezależnych wektorów w przestrzeni n-wymiarowej.

4. Rząd macierzy nie zmieni się jeżeli:

a)Wykreślimy wektor zerowy występujący w tej macierzy,

b)Wykreślimy jeden z dwóch wektorów współliniowych występujących w danej macierzy.

5. Rząd macierzy A nie zmieni się jeżeli:

a)Przestawimy ze sobą dwa wektory macierzy A,

b)Pomnożymy jeden z wektorów macierzy A przez liczbę α ∈ R (α ≠ 0),

c)Do jednego z wektorów macierzy A dodamy kombinacje liniową pozostałych wektorów tej macierzy.

6.rz(A^T)=rzA, tzn transpozycja nie zmienia rzędu danej macierzy

7. Rząd macierzy jest równy największemu spośród niezerowych podwyznaczników tej macierzy.

8. Praktyczna procedura wyznaczania rzędu macierzy sprowadza się do:

a)Przeprowadzenia eliminacji (zerowania) w wybranych wierszach lub kolumnach ,

b)Wykreślenia wektorów zerowych bądź wektorów współliniowych bez zmiany rzędu danej macierzy,

c)Tak długo aż otrzymamy podmacierz kwadratową i nieosobliwą, której rząd jest równy jej stopniowi.

39. Układy równań liniowych. Układy Cramera.

Układem m-równań liniowych o n-niewiadomych, nazywamy układ postaci:

a₁₁x_a + a₁₂x₂ + ... + a_1nx_n = b₁

a₂₁x₁ + a₂₂x₂ + ... + a_2nx_n = b₂

..............................................

a_m1x₁+ a_m2x₂ + ... + a_mnx_n = b_m

gdzie:

x₁, x₂, ..., x_n są niewiadomymi

b₁, b₂, ..., b_m są wyrazami wolnymi

aij jest współczynnikiem występującym w i-tym równaniu i przy j-tej niewiadomej

Mówimy, że jest to układ równań liniowych w tym sensie, że wszystkie niewiadome występują tylko, w pierwszej potędze i każde równanie ma postać addytywną (dodawanie).

Rozwiązaniem URL jest każde n-ka uporządkowana liczb rzeczywistych, które podstawione w miejsce niewiadomych spełniają wszystkie równania danego układu.

Postać macierzowa URL

Wprowadzając następujące oznaczenia wektorowe:

=
∈ Rⁿ - kolumnowy wektor niewiadomych,

=
∈ R^m - kolumnowy wektor wyrazów wolnych,

=
∈ R^m - kolumnowy wektor współczynników stojących przy j-tej niewiadomej

Wówczas:
x₁ +
x₂ + ... +
x_n =
. Jest to wektorowa postać URL, tzn. Kombinacja liniowa wektorów kolumnowych
o współczynnikach którymi są niewiadome, jest przyrównana do wektora wyrazów wolnych
.

Wprowadzając dodatkowo macierz A = [a_ij] _m×n zwaną macierzą główną URL, możemy zapisać URL w postaci równania macierzowego: A
=
.

Układy Cramera.

Układ : A
=
nazywamy układem Cramera ⇔ gdy macierz główna A jest kwadratowa i nieosobliwa, tzn(m=n) ∧ (detA≠0) Wówczas istnieje macierz odwrotna A^-1 do macierzy A i istnieje rozwiązanie równania macierzowego

A
=
/ A^-1 (lewostronnie)<=> A^-1 *A*
= A^-1 *b<=>
= A^-1
.- macierzowe rozwiązania układu Kramera(z wykorzystaniem macierzy odwrotnej)

TWIERDZENIE CRAMER'A: jeżeli URL A
=
jest układem Cramera to istnieje dokładnie jedno rozwiązanie w postaci wektora o n-składowych, opisanych wzorem:

X_k =
, k= 1, 2, ..., n

gdzie A_k jest macierzą powstającą

Twierdzenie C. mówi o istnieniu i jednoznaczności rozwiązania układu Cramera oraz podaje wyznacznikową metodę rozwiązania Teligo układu(metoda Cramera)

40. Niecramerowskie układy równań liniowych.

ukłC. <=>(m=n) ∧ (detA≠0)

ukł nieC <=>~[(m=n) ∧ (detA≠0)]<=>[(m≠n) v (detA=0)](def. komplementarna)

Mówimy o układzie niecramerowskim ⇔ gdy macierz główna A nie jest kwadratowa (m≠n) lub macierz główna jest kwadratowa ale osobliwa (detA = 0).

TWIERDZENIE KRONECKERA - CAPELLIEGO: URL A
=
posiada rozwiązanie ⇔ gdy rzA = rzU, gdzie U = [A¦
] jest tzw. macierzą uzupełnioną, powstającą przez dopisanie wektora wyrazów wolnych do macierzy głównej A.

a)warunek konieczny istnienia rozwiązania URL A
=
: Jeżeli istnieje rozwiązanie URL A
=
, to koniecznie musi być spełniony warunek rzA = rzU

b)warunek dostateczny: Jeżeli rzA = rzU, to istnieje rozwiązanie.

Układ równań może być:

1.sprzeczny (gdy nie istnieje rozwiązanie URL) ⇔ gdy rzA ≠ rzU(nie jest spełniony warunek konieczny istnienia rozwiązań)

2.oznaczony (gdy istnieje dokładni jedno rozwiązanie URL) ⇔ rzA = rzU = n (liczba niewiadomych)wówczas układ (mxn) redukujemy do zwykłego układy C(nxm)=> dokładnie jedno rozwiązanie (wektor n składowych) czyli układ oznaczony.

3.nieoznaczony (gdy istnieje nieskończenie wiele rozwiązań) ⇔ gdy rzA = rzU = r<n.

Wówczas (mxn) redukujemy do układy (rxr) traktując (n-r) nadwyżkowych niewiadomych jako parametry, tzn. zmienne swobodne można podstawić dowolne liczby rzeczywiste. Będzie to układ Cramera zależny od (n-r) parametru, stąd nieskończenie wiele ro

związań, czyli układ nieoznaczony.

41. Funkcja dwóch zmiennych - podstawowe pojęcia.

1. Definicja funkcji dwóch zmiennych: Jeżeli każdemu punktowi P(x,y) należącemu do przestrzeni R² =RxR tzn P∈ D ⊂ R² gdzie D jest pewnym zbiorem płaskim, przyporządkowana jest dokładnie jedna liczba rzeczywistą Z∈R to mówimy, że na zbiorze D określona została funkcja dwóch zmiennych x i y, i piszemy Z=f(x,y).

Inaczej mówiąc: argumentami tego odwzorowania są uporządkowane pary liczb rzeczywistych (x,y) ∈ D ⊂ R² , a wartościami są liczby rzeczywiste Z∈R.

2.Wykresem funkcji dwóch zmiennych, której dzidziną jest zbiór płaski D jest pewna powierzchnia przestrzeni trójwymiarowej R³, utworzona przez punkty o współrzędnych (x; y; z) ∈ R³, gdzie (x; y) ∈ D ⊂ R², natomiast z = f(x; y) ∈ R.

3.Pochodne cząstkowe funkcji dwóch zmiennych

Pochodna cząstkową funkcji Z=f(x,y) względem zmiennej x nazywamy granicę ilorazu różniczkowego funkcji f(x,y) dla przyrostu zmiennej Δx, gdy Δx →0, tzn

1)

Pochodna cząstkowa względem zmiennej x jest właściwą granicą ilorazu różniczkowego dla przyrostu Δx →0, przy czym drugą ze zmiennych traktujemy jako ustaloną. Analogicznie definiuje się pochodną cząstkową względem zmiennej y jako właściwą granicę ilorazu różniczkowego dla przyrostu Δy →0 traktując zmienna x jako ustaloną, tzn

2)

Oznacza to, że pochodne cząstkowe funkcji dwóch zmiennych obliczamy tak jak pochodną funkcji jednej zmiennej traktując drugą z nich jak stałą.

4.Interpretacja geometryczna pochodnych cząstkowych funkcji dwóch zmiennych.

Zakładamy, że funkcja Z=f(x,y) jest różniczkowalna w punkcie P₀(x₀; y₀) ∈ D ⊂ R² tzn istnieją obie pochodne cząstkowe w punkcie P₀.Czyli:

oraz

W interpretacji geometrycznej pochodna cząstkowa względem zmiennej x
) w punkcie Po jest przy ustalonym y=yo współczynnikiem kierunkowym stycznej do krzywej będącej przekrojem powierzchni(wykresu funkcji dwóch zmiennych) płaszczyzną prostopadłą do osi OY o równaniu y=yo

Analogicznie pochodna cząstkowa względem zmiennej y
) w punkcie Po współczynnikiem kierunkowym stycznej do krzywej będącej przekrojem powierzchni za pomocą płaszczyzny x=xo(dla ustalonej zmiennej xo)prostopadłej do osi OX.

W związku z tym pochodne cząstkowe nazywa się często pochodnymi kierunkowymi.

5.Pochodne cząstkowe drugiego rzędu.

Jeżeli pochodne cząstkowe funkcji dwóch zmiennych z = f(x; y) są określone w pewnym obszarze płaskim D, to możemy mówić o nowych funkcjach dwóch zmiennych określonych w zbiorze D, którymi są pochodne cząstkowe pierwszego rzędu. Możemy zatem mówić o pochodnych cząstkowych drugiego rzędu jako pochodnych cząstkowych pochodnych cząstkowych pierwszego rzędu.

a) -pochodna cząstkowa drugiego rzędu względem miennej x

b) -pochodna cząstkowa drugiego rzędu względem zmiennej y

c)

-pochodne cząstkowe drugiego rzędu mieszane

42. Ekstremum lokalne funkcji dwóch zmiennych.

Mówimy że funkcja dwóch zmiennych z = f(x; y) ma ekstremum lokalne w punkcie P₀(x₀; y₀) ⇔ gdy

٧ ٨ f(x; y) < f(x₀; y₀) - maksimum lokalne w punkcie P₀

δ>0 P∈S(P₀; δ)

٧ ٨ f(x; y) > f(x₀; y₀) - minimum lokalne w punkcie P₀

δ>0 P∈S(P₀; δ)

Zakładamy że istnieją pochodne cząstkowe pierwszego i drugiego rzędu funkcji z = f(x; y) w punkcie P₀ i pewnym jego sąsiedztwie S(P₀; δ).

1. Warunek konieczny istnienia ekstremum lokalnego funkcji z = f(x; y) w punkcie P₀(x₀; y₀):

f_x`(x₀; y₀) = 0
f_y'(x₀; y₀) = 0 - pochodne cząstkowe równe zero w punkcie P₀. Rozwiązanie tego układu równań w postaci P₀(x₀; y₀) dale tzw. punkty stacjonarne, które są kandydatami na ekstremum lokalne.

2. Warunek dostateczny istnienia ekstremum lokalnego funkcji dwóch zmiennych;

Budujemy tzw. wyróżnik:

W(x; y) = 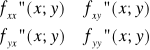


Warunkiem dostatecznym istnienia ekstremum lokalnego funkcji dwóch zmiennych z = f(x; y) w punkcie stacjonarnym P₀(x₀; y₀) jest dodatnia wartość wyróżnika w danym punkcie, przy czym znak pochodnej cząstkowej drugiego rzędu względem zmiennej x w punkcie P₀ pozwala wnioskować:

*W(x₀; y₀)>0 ∧ [f_xx”(P₀) > 0] =>minimum lokalne w punkcie P₀(x₀; y₀)

*W(x₀; y₀)>0 [f_xx”(P₀) < 0] => maksimum lokalne w punkcie P₀(x₀; y₀)

* W(x₀; y₀)<0 => ekstremum lokalne nie istnieje w punkcie P₀ (punkt siodłowy)

* W(x₀; y₀)=0 =>przypadek niekonkluzywny (nie rozstrzygniemy)

43. Ekstremum warunkowe funkcji dwóch zmiennych.

Poszukiwanie ekstremum warunkowego funkcji Z=f(x,y) przy warunku ϕ(x; y) = 0 oznacza poszukiwanie największej bądź najmniejszej wartości na powierzchni opisanej funkcją Z=f(x,y) wzdłuż pewnej trajektorii (ścieżki) wyznaczonej przez rzut krzywej płaskiej ϕ(x; y)=0 na powierzchnie (wykres funkcji dwóch zmiennych)

Warunek ϕ(x; y)=0 jest równanie opisujące pewną krzywą na płaszczyźnie XOY, a rzut tej krzywej na powierzchnie daje trajektorię wzdłuż której poszukujemy wartości największe lub najmniejsze (ekstremum warunkowe)

a)Warunek konieczny dla ekstremum warunkowego

Budujemy tzw. funkcję Lagrange'a postaci:

L(x; y; λ) = f(x; y) + λ*ϕ(x; y)

Jest to funkcja dwóch zmiennych x i y z parametrem λ zwanym mnożnikiem Lagrange'a.

a) warunek konieczny dla istnienia ekstremum warunkowego:

L_x'(x; y; λ) = 0
L_y'(x; y; λ) = 0
ϕ(x; y) = 0 (klamra)=> rozwiązując ten układ równań otrzymujemy punkt P₀(x₀; y₀) jako kandydata na ekstremum warunkowe oraz wartość mnożnika λ = λ₀ sprzężoną z punktem P₀.

b) warunek dostateczny dla ekstremum warunkowego w punkcie P₀ spełniającym warunek konieczny i sprzężonej z nim wartości mnożnika λ₀. Tworzymy wyróżnik oparty na pochodnych cząstkowych drugiego rzędu, opartych na funkcji Lagrange'a oraz na pochodnych pierwszego rzędu dla funkcji ϕ(x; y).

Δ(x; y; λ) =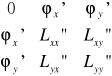

Warunkiem dostatecznym istnienia ekstremum warunkowego w punkcie P₀(x₀; y₀) dla mnożnika λ₀ jest różna od zera wartość powyższego wyznacznika, przy czym:

1. Δ( P₀; λ₀) > 0 ⇒ max. war w punkcie P₀
2. Δ( P₀; λ₀) < 0 ⇒ min. war w punkcie P₀

3. Δ( P₀; λ₀) = 0 ⇒ przypadek niekonkluzywny.

---