19 rafik, Politechnika Lubelska, Studia, Semestr 6, sprawka 6 sem moje

Politechnika Lubelska

w Lublinie

Laboratorium Napędu Elektrycznego

Ćwiczenie numer 19

Imię i nazwisko:

Rafał Masełko
Oskar Mazurek
Monika Masłyk
Mariusz Magdziak

Semestr

Grupa

6.2

Rok akademicki:

2011/2012

Temat ćwiczenia: Regulacja prędkości kątowej indukcyjnego silnika pierścieniowego w podsynchronicznych kaskadach przekształtnikowych.

Data wykonania:

24.04.2012

Ocena:

Cel ćwiczenia :

Celem ćwiczenia jest zapoznanie się z budową, zasadą pracy oraz charakterystykami układów kaskad podsynchronicznych.

Dane znamionowe :

Silnik pierścieniowy typ SZUe 44b Silnik prądu stałego typ PCMb 54b

P_n =4 kW P_n = 7,5 kW

U_n = 380 V U_n = 220 V

I_n = 8,6 A I_n = 39,2 A

n_n= 1425 obr/min n_n = 1450 obr/min

E_w = 103 V I_m = 0,93 A

I_w = 28 A

cosϕ = 0,82

Prądnica hamownicza typ PZMb 54b Transformator

P_n = 5,5 kw S_n = 6,6 kVA

U_n = 220 V U₁ = 380 V I₁ = 10 A

I_n = 28,8 A U₂ = 127 V I₂= 30 A

n_n = 1450 obr/min YyO

I_m = 0,714A

Schemat ideowy kaskady przekształtnikowej typu M = const. (ukł. zamknięty) :

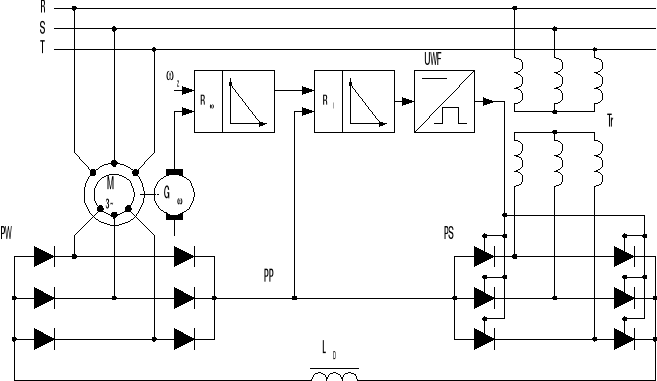
0x01 graphic

Oznaczenia na schemacie :

PW - prostownik wirnikowy; PS - falownik komutowany siecią;

UWF - układ wyzwalania falownika; R_ - regulator prędkości;

R_I - regulator prądu; PP - przekładnik prądowy;

Tr - transformator dopasowujący; L_DŁ - dławik wygładzający.

Charakterystyki mechaniczne kaskady typu M = const. (w układzie otwartym) :

a	U₁	I₁	P₁	U_w	I_d	I_tH		s	P_o	E_H	P_w	M		_p
^o	V	A	W	V	A	A	rad/s	-	W	V	W	Nm	-	-
400	400	5,4	50	40	1	0	41,87	0,73	158,98	88,8	158,98	3,80	0,31	0,01
		400	5,6	100	38	2	1	39,77	0,75	155,83	87,04	242,87	6,11	0,41	0,03
		400	6	100	36	3	2	37,68	0,76	152,69	85,28	323,25	8,58	0,31	0,02
		400	6,2	110	34	4	3	35,59	0,77	151,11	84,4	404,31	11,36	0,27	0,03
	800	400	5,5	100	100	1	0	104,67	0,33	147,96	80,65	147,96	1,41	0,68	0,03
		400	5,7	110	110	2	1	115,13	0,27	144,81	79,89	224,7	1,95	0,49	0,03
		400	6	150	150	3	2	157,00	0	140,09	78,25	296,59	1,89	0,51	0,04
		400	6,3	200	200	4	3	209,33	0	136,94	76,49	366,41	1,75	0,55	0,05
		400	6,5	200	200	5	4	209,33	0	120,36	31,65	183,27	0,88	-	0,04
		400	7	250	250	6	5	261,67	0	118,33	29,89	202,97	0,78	-	0,05
	1200	400	5,6	100	100	2	0,5	104,67	0	48,8	117,81	107,705	1,03	0,93	0,03
		400	5,8	150	150	3	1	157,00	0	42,5	110,35	152,85	0,97	0,98	0,04
		400	6,1	200	200	3,5	2	209,33	0	40,93	105,36	251,65	1,20	0,79	0,05
		400	6,6	250	250	5	4	261,67	0	37,78	100	437,78	1,67	0,57	0,05
		400	7,1	350	350	7	6	366,33	0	34,53	95,68	608,61	1,66	0,58	0,07

Przykłady obliczeń:

 =
=
==41,87 rad/s

s=
=
= 0,73

P_w= P_H+P₀= 0 + 158,58 =158,8 W

M.=
=
= 3,8 Nm

=
=
= 0,31

_p =
=
=0.01

Charakterystyki mechaniczne kaskady typu M = const. (w układzie zamkniętym )

a	U₁	I₁	P₁	U_w	I_d	I_tH		s	P_o	E_H	P_w	M		_p
^o	V	A	W	V	A	A	rad/s	-	W	V	W	Nm	-	-
400	400	5,4	50	40	1	0	41,87	0,73	160,33	90,12	160,33	3,83	0,31	0,01
		400	5,6	100	40	1,5	1	41,87	0,73	158,35	87,05	245,4	5,86	0,41	0,03
		400	5,8	100	40	3	2	41,87	0,73	156,35	86,44	329,23	7,86	0,30	0,02
		400	6,1	120	40	4	3	41,87	0,73	153,28	85,66	410,26	9,80	0,29	0,03
		400	6,3	140	40	5	4	41,87	0,73	148,98	81,44	474,74	11,34	0,29	0,03
	800	400	5,5	100	80	1	0	83,73	0,47	146,87	80	146,87	1,75	0,68	0,03
		400	5,7	110	80	2	1	83,73	0,47	140,09	79,22	219,31	2,62	0,50	0,03
		400	6	150	80	3	2	83,73	0,47	138,95	77,58	294,11	3,51	0,51	0,04
		400	6,5	200	80	4	3	83,73	0,47	132,33	40,77	254,64	3,04	0,79	0,04
		400	5,8	250	80	5	4	83,73	0,47	10,32	35,26	151,36	1,81	1,65	0,06
	1200	400	5,6	100	120	2	0	125,60	0,20	50,36	115,4	50,36	0,40	1,99	0,03
		400	6	150	120	3	2	125,60	0,20	48,56	106,55	261,66	2,08	0,57	0,04
		400	6,2	200	120	4	3	125,60	0,20	46,66	103,52	357,22	2,84	0,56	0,05
		400	6,6	300	120	5	4	125,60	0,20	44,52	99,33	441,84	3,52	0,68	0,07
		400	7	310	120	6	5	125,60	0,20	40,68	90,5	493,18	3,93	0,63	0,06

Charakterystyki : =f(M);M = f(I_d); = f(M);  f(M)

Schemat ideowy kaskady przekształtnikowej typu P = const. (ukł. otwarty) :

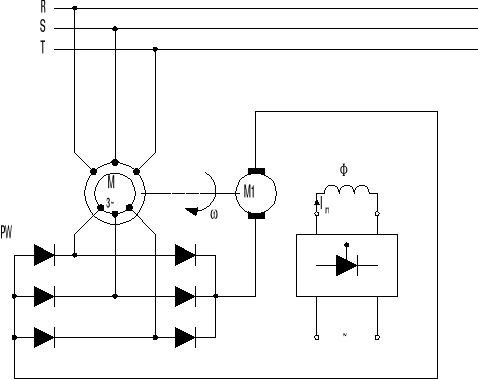
0x01 graphic

Charakterystyki mechaniczne kaskady typu P = const.

Wyniki pomiarów i obliczeń :

a	U₁	I₁	P₁	U_w	I_d	I_tH	I		s	P_o	E_H	P_w	M		_p
^o	V	A	W	V	A	A	A	rad/s	-	W	V	W	Nm	-	-
400	400	5	100	140	2	0	0	146,53	0,07	160,33	90,12	160,33	1,09	0,62	0,03
		400	5	150	138	3	1	0	144,44	0,08	158,35	87,05	245,4	1,70	0,61	0,04
		400	5	200	138	4	2	0	144,44	0,08	156,35	86,44	329,23	2,28	0,61	0,06
		400	5	250	138	5	3	0	144,44	0,08	153,28	85,66	410,26	2,84	0,61	0,07
		400	5	300	137	6	4	0	143,39	0,09	148,98	81,44	474,74	3,31	0,63	0,09
	800	400	5	100	108	1	0,5	0,15	113,04	0,28	146,87	80	186,87	1,65	0,54	0,03
		400	5	110	108	2	1	0,15	113,04	0,28	140,09	79,22	219,31	1,94	0,50	0,03
		400	5	150	108	3	2	0,15	113,04	0,28	138,95	77,58	294,11	2,60	0,51	0,04
		400	5	200	108	4	3	0,15	113,04	0,28	132,33	40,77	254,64	2,25	0,79	0,06
		400	5	250	108	5	4	0,15	113,04	0,28	10,32	35,26	151,36	1,34	1,65	0,07
	1200	400	5	50	74	1	0	0,55	77,45	0,51	50,36	115,4	50,36	0,65	0,99	0,01
		400	5	100	74	1	2	0,55	77,45	0,51	48,56	106,55	261,66	3,38	0,38	0,03
		400	5	150	74	2	3	0,55	77,45	0,51	46,66	103,52	357,22	4,61	0,42	0,04
		400	5	150	74	2	4	0,55	77,45	0,51	44,52	99,33	441,84	5,70	0,34	0,04
		400	5	200	74	3	5	0,55	77,45	0,51	40,68	90,5	493,18	6,37	0,41	0,06

Charakterystyki:  = f(M); M = f(I_d);  = f(M);  = f(M)

0x01 graphic

Wnioski:

Prędkość obrotowa kaskad podsynchronicznych zależy od kąta sterowania zaworów prostownika. Zależności te są jednak różne dla obu badanych typów kaskad. Dla kaskady typu M = const. prędkość obrotowa maleje wraz ze wzrostem kąta sterowania, natomiast dla kaskady typu P = const. prędkość obrotowa wzrasta.

W układach kaskady typu M = const. można zaobserwować spadek prędkości obrotowej maszyny wraz ze wzrostem momentu oporowego. Dla wartości małych i średnich momentu spadek prędkości jest proporcjonalny do wzrostu momentu, przy większych wartościach momentu oporowego prędkość spada znacznie gwałtowniej. Przy czym należy zauważyć fakt, że odcinki liniowe charakterystyk dla różnych kątów sterowania są do siebie równoległe, ale odcinek gwałtowniejszego spadku przy większych wartościach momentu jest tym łagodniejszy im większy jest kąt sterowania zaworów. Im większy jest kąt sterowania tym charakterystyka przebiega niżej (mniejsze prędkości obrotowe).

Charakterystyki kaskady typu P = const. są podobne do omówionych wcześniej (co do przebiegu). Z tą jednak różnicą, że kaskada tego typu największe prędkości rozwija dla największego kąta sterowania, jak również dla największego kąta sterowania stromość spadku prędkości dla większych wartości momentu oporowego jest największa.

Błędem popełnionym przez nas podczas wykonywania ćwiczenia jest to, że przy układzie otwartym i zamkniętym nie mieliśmy jednakowych nastaw kąta sterowania. Wpłynęło to na przebieg porównania charakterystyk.