Kurpiel Marek Warszawa 26.11.2002

Zi-14b

WOJSKOWA AKADEMIA TECHNICZNA

STATYCZNE METODY POMIARU NA GLOBIE ZIEMSKIM I ZWIĄZEK Z NIMI

GEODEZJA - (geōdasia - od greckiego ğe Ziemia, daiomi - dzielę). Pojęcie to wprowadził grecki filozof Arystoteles (IV w. p.n.e.). Jest to jedna z nauk o Ziemi mająca na celu wyznaczenie jej kształtu i rozmiarów oraz nadanie im wyrazu matematycznego i liczbowego, co sprowadza się do wyznaczenia powierzchni zamkniętej najbliższej rzeczywistym kształtom bryły ziemskiej, którą można opisać równikiem i do nadania parametrom tego równania wartości liczbowych.

Geodezja jest to nauka o pomiarach Ziemi wykonywanych w celu:

• wyznaczeniu kształtu i wielkości jej części lub całości,

• sporządzania map geodezyjnych, wykorzystania tych pomiarów do różnych prac geodezyjnych i gospodarczych.

Przedmiotem pomiarów są najczęściej kąty poziome i pionowe, odległości, różnice wysokości, przyspieszenie ziemskie oraz współrzędne geograficzne.

Efektem prac geodezyjnych są najczęściej mapy.

Prace geodezyjne można podzielić najogólniej na cztery etapy:

1. Prace (pomiary) polowe polegające na bezpośrednim pomiarze w terenie za pomocą różnych geodezyjnych instrumentów i przyrządów (teodolitu, niwelatora, taśmy mierniczej, łaty niwelacyjnej, dalmierza optycznego lub elektrooptycznego, grawimetru itd.).

2. Prace obliczeniowe polegające najczęściej na wyznaczaniu współrzędnych punktów geodezyjnych na podstawie wielkości pomierzonych.

3. Prace graficzne polegające na przedstawieniu wyników pomiarów w postaci map geodezyjnych lub profilów. Ta część prac geodezyjnych łączy się z kartografią, która jest związana z nauką o mapach, metodach ich sporządzania i sposobach ich wykorzystania.

4. Obliczenia pola powierzchni mierzonych powierzchni.

Geodezja bardzo silnie powiązana jest z życiem i rozwojem ludzi. Ślady zachowanych pierwszych dokumentów pisanych, związanych z geodezją pozostawiły już najstarsze cywilizacje (sumeryjska, egipska, chińska, indiańska). Istnieją dowody na to, że światlejsi przedstawiciele tamtych cywilizacji dokonywali pewnych obserwacji związanych z ruchem wirowym i ruchem orbitalnym Ziemi oraz podejmowali próby tworzenia modeli objaśniających obserwowane zjawiska astronomiczne. Modele te musiały dotyczyć również kształtu Ziemi. Historię geodezji można podzielić na następujące okresy:

• Okres prehistorycznych (wyobrażenia ludzi o kształcie ziemi)

• Okres geodezji geometrycznej od starożytnych Greków (ok. 600 p.n.e.) aż do połowy XVII w. (do sformułowania przez Newtona prawa powszechnej grawitacji). W tym okresie zainteresowania badaczy skupiły się na poznaniu rozmiaru "kulistej Ziemi".

• Okres rozwoju geodezji fizycznej (od Newtona do połowy XX w.) Odkrycie grawitacji i siły odśrodkowej sprawiło, że metody geodezji dynamicznej były podstawowym narzędziem badania figury ziemi.

• Okres geodezji współczesnej w epoce rewolucji technologicznej: elektronicznych komputerów, telekomunikacji, laserów i sztucznych satelitów Ziemi.

Okres geodezji geometrycznej - początki sięgają VI w. p.n.e. Około II w. wcześniej Homer (około 800 p.n.e.), a później Tales z Miletu (600 p.n.e.) pisali o ziemskiej tarczy otoczonej oceanami.

Jednak niedługo potem Pitagoras (około 580-500 p.n.e.) określił Ziemię jako ciało sferyczne a podtrzymał tę tezę największy filozof i uczony starożytnego świata Arystoteles (348-315), uważany za ówczesnego eksperta w wielu dziedzinach, który przy wyciąganiu wniosków uwzględniał zarówno obserwacje empiryczne jak i logiczne rozumowanie. To właśnie temu myślicielowi przypisuje się jako pierwszemu zainteresowanie ziemską grawitacją. Środowisko greckich astronomów już w VI w p.n.e. przyjmowało sferyczny kształt księżyca i opisywało ruchy obrotowe słońca i księżyca a w wieku IV p.n.e. dysponowali rokiem zwrotnikowym trwającym 365,25 dób.

Natomiast Grek Pytaes podejrzewał (ok. III w. p.n.e.) że przypływy morskie powodowane są przez ciała niebieskie. Jako pierwszy wyznaczył szerokość geograficzną, a w 150 lat później Hipparch opracował pierwszą mapę nieba w systemie ekwinokcjalnym (ekwinokcjum - równonoc- zrównanie dnia z nocą).

„Naukowy początek” geodezji najczęściej wiąże się z greckim filozofem, astronomem, matematykiem i geografem Eratostenesem, który jako pierwszy wyznaczył "kąt nachylenia eliptyki do równika niebieskiego". Wyznaczył również promień ziemski poprzez pomiar długości łuku południka.

Około 235 roku grecki astronom z Cyrene został powołany przez Ptolemeusza III Euergetesa na stanowisko dyrektora biblioteki aleksandryjskiej. Dostrzegł on, że w czasie równonocy wiosennej promienie słoneczne padają pionowo w miejscowości Syene (dzisiejszy Asuan). Potwierdziło to odbicie lustrzane promieni słonecznych w bardzo głębokiej studni. W tym samym czasie kolumna w Aleksandrii rzucała najkrótszy cień w roku. Wywnioskował wtedy, że słońce świeci wówczas w zenicie. Przekonał się o tym po sprawdzeniu gnomonem (najstarszym instrumentem astronomicznym w postaci pionowego pręta lub słupa ustawionego na podstawie; według długości jego cienia wyznaczano deklinację i azymut słońca). Pomierzywszy wysokość kolumny i długość jej cienia, Eratostenes ustalił, że kąt jaki tworzą słoneczne promienie z kolumną wynosi 0,2 kąta pełnego tzn. γ = 7˚12′. Była to długość łuku południka między Syene a Aleksandrią i wynosiła ok. 790 km. Eratostenes zdawał sobie sprawę, że tak duża odległość jest korzystna dla dokładnego wyznaczenia promienia ziemskiego. Z drugiej zaś strony wiedział, iż dokładny pomiar w ówczesnych czasach tak dużego łuku na globie ziemskim jest niewykonalny. Erastostenes wykorzystał również istniejące już wcześniej „precyzyjne pomiary katastralne” pól uprawnych w dolinie Nilu za pomocą których wyznaczył czas przemarszu „wielbłądziej karawany” przez znaną z pomiarów odległość. Po zastosowaniu obu metod uczony wyznaczył odległość studni od kolumny na około ∆Ł=5000 stadiów egipskich. Po wykonaniu niezbędnych obliczeń określił promień Ziemi na R=6267 km (1 stadia = 157,5 m). Mimo, iż nie jest to dokładny wynik z powodu zastosowania mało precyzyjnych metod pomiaru to i tak nie umniejsza to genialności pomysłu Eratostenesa. Blisko 50 lat później Poseydonius otrzymał wynik o 11% różniący się od średniego promienia Ziemi. W następnym tysiącleciu, około roku 870 Kalif al - Mamunu wykonał pomiary w okolicach Bagdadu otrzymując długość promienia o 10% za dużą w stosunku do obecnej średniej wartości, tzn. w stosunku do 6371 km. Epokę wielkich Greków kończą dzieła Ptolemeusza (około 75-151), które stanowią podsumowanie ówczesnej wiedzy z zakresu geodezji i astronomi zgromadzonej w Aleksandrii pod znanym tytułem arabskim „Almagest” i „Wstęp do geografii oraz słynna mapa świata, na której po raz pierwszy pokazano (najstarsze) polskie miasto Kalisz (Calisia), położone na szlaku bursztynowym. Ptolemeusz jednak nie akceptował teorii heliocentrycznej głoszonej przed nim za czasów Heraklidesa. Po okresie przestoju, który trwał do początku renesansu nastąpił rozkwit nauki i sztuki. Wielkie podróże u schyłku XIII w. (Marco Polo, 1271-95), nowa mapa świata, którą opracował Toscanelli (1397-1482), ożywienie
kulturalne i gospodarcze, w XV w. wynalezienie druku (Gutenberg,1455), odkrycie Ameryki (Kolumb 1492), opłynięcie świata (Amerigo Vespucci 1452-1512). Nie można było już zaprzeczyć sferycznemu kształtowi ziemi.

W roku 1530 polski uczony z Torunia, Mikołaj Kopernik ukończył pracę nad swoim dziełem „De revolutionibus orbium coelestium” (,,O obrotach sfer niebieskich”) dając światu naukowo uzasadnioną teorię heliocentryczną. Udowadniał on, że Słońce stanowi nieruchome centrum, wokół którego krążą planety. Pomimo dużych utrudnień ze strony władz kościelnych Kopernik opracował szczegółowo matematyczną stronę swej hipotezy przekształcając ją w sposób użyteczny dla dalszego rozwoju nauki. Nieścisłością jednak był fakt, iż ten wielki astronom uważał orbity planet za okrągłe.Wkrótce potem niemiecki astronom Jan Kepler wyznaczył z obserwacji i ogłosił swoje trzy prawa, ruchu planet ugruntowując teorię Kopernika i uściślając ją (kopernikańskie orbity - okręgi zostały zastąpione keplerowskimi elipsami). W tym samym czasie w Padwie Galileusz (Galileo Galilei) badał ruch ciał pod wpływem siły grawitacji. Urodzony 15 lutego 1564 roku w Pizie wstąpił na tamtejszy uniwersytet, by studiować medycynę. Do tego czasu jego wiedza matematyczna była znikoma. Galileuszowi dane było jednak wysłuchać wykładu z geometrii, który tak go zainteresował, że jego uwaga zwróciła się ku matematyce i naukom ścisłym. W roku 1586 opublikował pracę z dziedziny hydrostatyki, która przyniosła mu rozgłos w kręgach naukowych. Dzięki pracy o środku ciężkości (która ukazała się w 1589 roku) otrzymał stanowisko wykładowcy matematyki w Pizie. Galileusz był głęboko przekonany o słuszności heliocentrycznej teorii Kopernika. Jednak jak wyznał w liście do Keplera, ukrywał swe przekonania, by nie narazić się na kpiny ze strony innych przedstawicieli świata ówczesnej nauki.

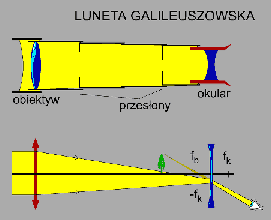
W 1609 roku Galileusz, odwiedziwszy Wenecję dowiedział się o nowym wynalazku - teleskopie. Rok wcześniej przyrząd taki zbudował Holender Hans Lippershey. Zaraz po powrocie do Padwy Galileusz skonstruował dla siebie ulepszoną wersję tego przyrządu optycznego. Opracował przy tym metodę wyznaczania promienia krzywizny soczewek. Wkrótce teleskop Galileusza stał się jednym z podstawowych przyrządów naukowych, nawigacyjnych i obserwacyjnych.

Uzbrojony w nowe potężne narzędzie badawcze, Galileusz rozpoczął badania nieba i wreszcie zaczął ogłaszać swe odkrycia. Stwierdził, że powierzchnia Księżyca nie jest gładka, jak dotychczas twierdzono, że Droga Mleczna składa się z mnóstwa gwiazd, i że Jowisz posiada własne satelity. Szczególnie ważne było to ostatnie, dowodziło bowiem, że, Ziemia nie jest jedynym ciałem niebieskim wokół którego krążą inne ciała. Obserwował także takie zjawiska i obiekty jak plamy na Słońcu, fazy Wenus, pierścienie Saturna - a swe odkrycia opublikował w dziele Siderius nuntius w 1610 roku. Opublikowanie w 1632 r. książki Dialogo dei Massimi Sistemi (Dyskusja o systemach niebieskich), w której popierał kopernikańskie i ptolemejskie poglądy na temat ruchu planet doprowadziło do zadenuncjowania Galileusza do świętej inkwizycji w roku 1633 w Rzymie prawie siedemdziesięcioletni, na wpół ślepy Galileusz został zmuszony do odwołania swoich poglądów i wyparcia się tez, które prezentował w swojej książce. Na łożu śmierci mamrotał „...eppur si muove” („...a jednak się kręci”). Dzieła Galileusza (także Keplera i Kopernika) dopiero w roku 1822 zdjęto z indeksu ksiąg zakazanych.

Descartes Rene, Kartezjusz (1596-1650), wybitny filozof, racjonalista oraz matematyk i fizyk francuski, prekursor współczesnej kultury umysłowej, postulował metodę rozumowania wzorowaną na myśleniu matematycznym, twórca kartezjanizmu oraz słynnej sentencji „cogito ergo sum”- myślę więc jestem, głosił mechanistyczną i deterministyczną koncepcję przyrody, nawet ożywionej.

W dziele Geometria (1637) stworzył podstawy geometrii analitycznej, wprowadził podstawowe pojęcia matematyczne takie jak: zmienna niezależna, funkcja, układ współrzędnych prostokątnych. Układ współrzędnych, który na płaszczyźnie tworzą dwie, a w przestrzeni trzy wzajemnie prostopadłe proste - noszą nazwę osi układu, a miejsce ich przecięcia jest jego początkiem. Położenie punktu określa się przez podanie odległości od początku układu do punktów otrzymanych przez rzutowanie prostopadłe danego punktu na poszczególne osie (układ wprowadził w XVII w. R.Descartes). Kartezjusz opracował podstawowe twierdzenie algebry. W dziedzinie fizyki sformułował prawo zachowania pędu oraz odbicia i załamania światła.

Geograficzne współrzędne - sferyczne współrzędne punktów na ziemi:

1. Długość geograficzna, kąt dwuścienny między płaszczyznami południków, z których jedna przechodzi przez Greenwich Obserwatory na przedmieściu Londynu, a druga przez dany punkt na Ziemi (punkty leżące na wschód od południka Greenwich mają długość geograficzną ujemną lub wschodnią, często oznaczoną E, natomiast punkty leżące na zachód - dodatnią lub zachodnią, często oznaczoną W).

2. Szerokość geograficzna - kąt między kierunkiem pionu w danym punkcie na Ziemi, a płaszczyzną równika (punkty leżące na północ od równika mają szerokość geograficzną dodatnią lub północną, często oznaczoną N, punkty leżące na południe od równika - ujemną lub południową, często oznaczoną S).

W tym samym czasie (XVI w.) flamandzki kartograf Gerhard Mercator (1512-1594) wychodząc naprzeciw potrzebą nawigacji opracował swoją mapę świata. Jako pionier i orędownik naukowo opracowanych odwzorowań konforemnych, jest uważany za ojca nowoczesnej kartografii. Inne doniosłe odkrycie (1615 r.), które zrewolucjonizowało naziemne pomiary geodezyjne a także wyznaczanie wymiaru i kształtu Ziemi na ponad trzy stulecia to triangulacja stworzona jako metoda pomiaru Ziemi przez holenderskiego geodetę, matematyka i fizyka Willebrordusa Snelliusa - Snell van Royen (1580-1626). Triangulacja polegała na wyznaczaniu współrzędnych punktów na terenie za pomocą układów trójkątów tzw. Sieci triangulencyjnych, w których mierzy się wszystkie kąty oraz jeden lub kilka boków tzw. baz. Wyniki pomiaru stanowią podstawę geodezyjnych pomiarów poziomych oraz służą do wyznaczania elipsoidy ziemskiej i geoidy. Na ich podstawie Sinellius wyznaczył długość południka (1615-1617). Sformułował prawa optyki geometrycznej. W roku 1670 francuski duchowny Picard po dziewiętnastu stuleciach od słynnego eksperymentu Eratostenesa dokonał z inicjatywy nowo powołanej (1666r) Francuskiej Akademii Nauk nowoczesnych pomiarów łuku południka ziemskiego (paryskiego). Za pomocą triangulacji osiągnął wynik R=6275 km. Także Picard jako pierwszy zastosował krzyż kresek do celowania w lunecie instrumentu. Okres geodezji fizycznej oznacza w rozwoju geodezji przejście od sferycznego do elipsoidalnego modelu Ziemi, takiego modelu, z jakiego korzystamy po dzień dzisiejszy. Okres ten rozpoczyna największe (najprawdopodobniej) odkrycie naszej ery Isaaka Newtona „prawo powszechnej grawitacji” z roku 1687. Isaak Newton - Sir urodził się 25 grudnia 1642r. na farmie niedaleko Grantham w Anglii. W szkole z początku uczył się nienajlepiej, jednak potem zmienił się i został najlepszym uczniem w szkole. W 1660 roku wuj umożliwił mu powrót do szkoły, celem przygotowania do ubiegania się o przyjęcie do Kolegium Św. Trójcy uniwersytetu w Cambridge. Ukończył je w roku 1665, a dwa lata później został wybrany członkiem kolegium.

Najważniejsze z odkryć Newtona z tego okresu to z pewnością rachunek różniczkowy. Również fizyka zyskała na pobycie Newtona w domu. Stwierdził on wówczas, że białe światło przechodzące przez pryzmat, ulega rozczepieniu na tęczę kolorów (Newton używał słowa spektrum). Można je było z kolei z powrotem przekształcić w światło białe, używając drugiego pryzmatu. Jednak najgenialniejszym pomysłem Newtona była teoria, że księżyc jest utrzymywany w swej orbicie przez siłę wywieraną nań przez Ziemię. Siłę tę, o której sądzono wcześniej, że ma związek z magnetyzmem, nazwał grawitacją. Po latach Newton rzekomo wyjaśniał, że na swój pomysł wpadł obserwując w przydomowym sadzie spadające z drzewa jabłko. Newton założył, że przyspieszenie w swobodnym spadaniu jest proporcjonalne do siły grawitacji, a sama siła jest odwrotnie proporcjonalna do kwadratu odległości między oddziałującymi obiektami. Na tej podstawie przeprowadził obliczenia, które pokazywały, jak wyglądałby ruch Księżyca, gdyby założenia były prawidłowe. Niestety, dostępne wówczas dane dotyczące rozmiarów Ziemi były fałszywe i spowodowały, że rezultaty teoretycznych rozważań nie były satysfakcjonujące, a Newton nie zdecydował się na opublikowanie swojej idei. Zrobił to dopiero 20 lat później.

W 1667 roku zaproponowano mu objęcie stanowiska profesora matematyki w Cambridge (miał wówczas 26 lat!). Newton równolegle konstruował teleskop. Jego doświadczenia z pryzmatem, a potem z soczewkami utwierdziły go w przekonaniu, że niemożliwym będzie wyprodukowanie takich soczewek, które będą pozbawione wady aberracji chromatycznej przejawiającej się kolorowymi obwódkami wokół obserwowanych obiektów. Wady tej nie miały lustra i dlatego Newton zdecydował się zastąpić wklęsłym lustrem soczewkę powiększającą. W ten sposób powstał reflektor - teleskop zwierciadlany. Obraz oglądano w nim przez niewielki okular umieszczony z boku rury teleskopu. Oryginalny teleskop zbudowany przez Newtona miał 9 cali długości i lustro o średnicy dwóch cali. Jest to dziś jeden z najcenniejszych eksponatów w posiadaniu Towarzystwa Królewskiego w Londynie. Niedługo potem Newton przesłał do Towarzystwa Królewskiego swą pracę dotyczącą światła i barw. Ta spotkała się z ostrą krytyką, szczególnie ze strony Roberta Hooke'a (1635-1703). Newton pisał w 1675 roku:,,Dyskusje powstałe w związku z moją teorią światła prześladowały mnie do tego stopnia, że zacząłem oskarżać się o nieroztropność, która doprowadziła mnie do utraty błogosławieństwa, jakim jest spokój i usunąłem się w cień”. W rezultacie jego traktat o optyce (Opticks) ukazał się dopiero w 1704 r., zaraz po śmierci Hooke'a. Biorąc pod uwagę te wątpliwości, Newton przeprowadził jednak dalsze badania nad światłem. Według niego światło to małe cząsteczki poruszające się z wielką prędkością. Dzięki tej teorii był w stanie wyprowadzić prawa odbicia i załamania światła z mechaniki. Newton wyjaśnił, skąd biorą się kolorowe pierścienie widoczne, gdy światło odbija się od cienkich błon, jak na przykład bańka mydlana, lub powstające, gdy duża wypukła soczewka spoczywa na płaskiej powierzchni odbijającej światło. To ostatnie zjawisko nazywamy do dziś ,,pierścieniami Newtona”. Przez wiele lat Newton prowadził swoje poszukiwania matematyczne, nie publikując rezultatów.

W styczniu 1684 roku na posiedzeniu Towarzystwa Królewskiego astronom Edmund Halley (1656-1742) wdał się w rozmowę z Robertem Hooke'iem i architektem Christopherem Wrenem (1632-1723). Hooke stwierdził, że Newton ,,pokazał wszystkie prawa rządzące ruchem ciał niebieskich”. Gdy Halley okazał niedowierzanie, Wren zaoferował nagrodę każdemu, kto w ciągu dwóch miesięcy przedstawi przekonującą teorię.

Jednak dopiero w grudniu 1684 roku Wren mógł ogłosić Towarzystwu, że Newton napisał traktat De Motu Corporum (O ruchu ciał). W tym samym czasie Newton rozpoczął pisanie swej pracy Philosophiae Naturalis Principia Mathematica (Matematyczne podstawy nauk przyrodniczych), która ukazała się w 1687 roku. W pracy tej znalazły się następujące trzy prawa ruchu, zwane dziś także zasadami dynamiki Newtona:

1. Każde ciało kontynuuje ruch ze stałą prędkością po prostej, dopóki nie zostanie zmuszone do zmiany tego stanu przez działającą siłę.

2. Zmiana ruchu jest równa co do wielkości działającej sile (ruchem nazwano wówczas pęd - iloczyn masy i prędkości, zmiana pędu jest iloczynem masy i przyspieszenia - oczywiście jeśli nie zmieniamy masy ciała).

3. Siły są efektem wzajemnego oddziaływania ciał (jak na przykład grawitacja), a więc siła, z jaką jedno ciało działa na drugie, jest równa co do wielkości, lecz przeciwnie skierowana do siły, z jaką to drugie ciało działa na pierwsze.

Jakie są implikacje tych zasad? W pierwszej zawarte są dwie istotne idee. Jedną jest bezwładność, tendencja ciał do pozostawania w takim stanie, w jakim się znajdują, niezależnie czy jest to ruch po prostej, krążenie po orbicie czy pozostawanie w spoczynku. Drugą jest to, że zmianę stanu powoduje siła. Gdy działa zgodnie z kierunkiem ruchu, powoduje ona jedynie zmianę prędkości ruchu (zwiększenie lub zmniejszenie). Gdy siła działa pod kątem do kierunku ruchu, należy ją rozłożyć na siły składowe: równoległą do ruchu i prostopadłą doń. Składowa równoległa jest odpowiedzialna za zmianę wartości prędkości ruchu, prostopadła zaś powoduje zmianę kierunku ruchu. Od poznania zasad tego rozkładu sił zależy powodzenie przy stole bilardowym.

Druga zasada mówi, że im większa siła, tym większe może nadać ona przyspieszenie danemu ciału. Newton nie był pewny, czym w sensie fizycznym jest masa (Boyle wcześniej sugerował, że jest ona ściśle związana z liczbą atomów bądź cząsteczek składających się na dane ciało), więc odróżnił masę od ciężaru. Ciężar, jak stwierdził, jest efektem działania na ciało siły grawitacyjnej. Z tej racji ciężar człowieka na Księżycu jest kilkakrotnie mniejszy od ciężaru tej osoby na Ziemi. Tak więc ciężar to masa pomnożona przez przyspieszenie grawitacyjne.

Trzecia zasada dynamiki bywa często wyrażana w znanej formule: każda akcja powoduje przeciwną reakcję. Książka leżąca na stole działa na stół skierowaną w dół siłą nacisku równą ciężarowi, jednocześnie stół z taką samą siłą działa na książkę. Siła ta utrzymuje książkę na stole, nie pozwalając jej opaść na ziemię.

Trzecia zasada dynamiki wyjaśnia także, dlaczego rakieta może podróżować w przestrzeni kosmicznej w warunkach próżni. Gazy wytwarzane w silniku podczas spalania paliwa wylatują przez dyszę z pewnym przyspieszeniem - rakieta wywiera na gaz pewną siłę. Jednocześnie gazy wywierają na rakietę siłę taką samą, lecz skierowaną w przeciwną stronę. Wskutek tego rakieta leci do przodu. Podobne zjawisko zauważymy, gdy stojąc na wrotkach lub deskorolce, wyrzucimy ciężki przedmiot. W efekcie zaczniemy poruszać się w stronę przeciwną do kierunku rzutu.

Rozwijając trzecią zasadę Newton wysunął następną tezę, potwierdzenie idei i rozwinięcie, która narodziła się dwadzieścia lat wcześniej, jak twierdzą niektórzy w sadzie jabłoniowym. Było to prawo grawitacji: dwa ciała przyciągają się wzajemnie z siłą wprost proporcjonalną do iloczynu ich mas, a odwrotnie proporcjonalną do kwadratu odległości między nimi.

Wykorzystując te prawa, Newton mógł teoretycznie potwierdzić prawa ruchu planet, zwane prawami Keplera - odkrył je Jan Kepler (1571 - 1630) około roku 1600 w drodze żmudnych i precyzyjnych obserwacji. Tym razem Newton dysponował znacznie dokładniejszymi danymi na temat rozmiaru i masy Ziemi niż 20 lat wcześniej i udało mu się zweryfikować teorię grawitacji. W 1699 roku Isaaka Newtona powołano na stanowisko naczelnika mennicy, które zajmował do końca życia. W 1705 roku nadano mu tytuł szlachecki. Zmarł 20 marca 1727 roku.

O Newtonie pisał poeta Alexander Popem: ,,rzekł Bóg <<Niech się stanie Newton>> i światło padło na prawa Natury”. W dwudziestym wieku inny poeta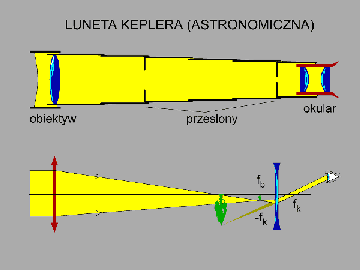
dodał wersy: ,,Nie trwało to zbyt długo, Szatan krzyknął <<Ho! Niech się stanie Einstein>> i przywrócił status quo”.

Wydawać by się mogło, że einsteinowska teoria względności na zawsze pogrzebała zasady dynamiki Newtona. Okazało się bowiem, że w pewnych warunkach wielkości przyjęte przez Newtona za stałe stają się względne. Jednak w praktyce teorię Einsteina można traktować jako uogólnienie zasad Newtona, które wciąż pozostają prawdziwe w świecie ciał poruszających się prędkościami znacznie mniejszymi od prędkości światła.

Newtona liczba, Ne - liczba znamienna charakteryzująca podobieństwo dynamiczne układów, w których pod działaniem siły występuje ruch. Ne = Ft/(mv), gdzie F oznacza siłę, t - czas, m - masę, v - prędkość liniową.

Newtona pierścienie - jedno ze zjawisk świetlnych wynikających z interferencji światła (interferencja fal).

Przejście od sferycznego do elipsoidalnego modelu Ziemi zaczyna się w czasie największego odkrycia naszej ery. W bardzo dużym stopniu nie tylko do rozwoju geodezji, ale również wielu innych dziedzin nauki przyczynił się wielki uczony naszej ery Isaak Newton. Pierwszą opublikowaną, ważną pracą były jego przełomowe badania nad naturą świata. Odkrył, że zwykłe światło białe tak naprawdę jest mieszanką wszystkich barw tęczy. Starannie prowadzone badania nad załamaniem odbiciem światła doprowadziły do skonstruowania pierwszego teleskopu zwierciadlanego używanego do dzisiejszych czasów. Odkrył i opracował rachunek całkowy, który stanowi nie tylko fundament współczesnej nauki matematycznej, ale również narzędziem, bez którego trudno sobie wyobrazić dalszy postęp w nauce. Należy wspomnieć o bardzo ważnych osiągnięciach w dziedzinie mechaniki - nauce o ruchach ciał. To właśnie Isaak Newton sformułował trzy zasady dynamiki wyjaśniające wiele dotąd nie odgadnionych praw, jakimi rządzi się otaczający świat. Najsłynniejszym jednak naukowym prawem jest prawo powszechnego ciążenia. Dzięki tym prawom tworzącym jednolity system można wyjaśnić i przewidywać działanie wszystkich makroskopowych układów mechanicznych (od poruszającego się wahadła do ruchu planet na ich orbitach). Isaak Newton szczegółowo opisał prawa te w swoim dziele „Philosophiae naturalis principia mathematica” (matematyczne zasady filozofii przyrody) opublikowanym w 1687 r.

Isaak Newton poczynił również duży wkład w innych dziedzinach nauki np.: termodynamice i akustyce. Jego odkrycia stanowią niewątpliwie próg, który dzieli naukę w postaci zlepka luźnych praw i faktów, a nowym torem na jaki pokierował nowoczesna naukę Isaak Newton. O Newtonie pisał poeta Aleksander Popem „Nature and Natures laws lay hid in night: God said, let Nevton be and all was light (Natura i prawo natury tkwiły ukryte w ciemnościach: rzekł Bóg: „niech stanie się Nevton” i światło padło na prawa Natury.

Carll Gauss - ten książę matematyków uważany jest za ojca nowoczesnej geodezji. Wynalazł heliotrop - przyrząd geodezyjny kierujący wiązkę światła słonecznego lub sztucznego ku określonemu obiektowi. W istotnym stopniu przyczynił się do rozwoju teorii liczb i geometrii. W trakcie pomiarów i analizy „triangulacji hanowerskiej” dał podstawy teorii błędów i ruchu, teorii prawdopodobieństwa i statystyki, opracował metody obliczeń geodezyjnych na elipsoidzie, wniósł duży wkład do astronomii i elektromagnetyzmu oraz kartografii i miernictwa. Sformułował zasadę geometrii nieeuklidesowej.

Aby prawidłowo opisać zakrzywienie powierzchni ziemskiej Gauss zastosował wiele metod matematycznychjedną spośród nich było odwzorowanie konforemne. Ponadto pozostawił metody i wzory stosowane po dzień dzisiejszy w mechanice nieba orbit sztucznych satelitów Ziemi. Zawdzięczamy mu definicję geoidy.

Zasada Gaussa, w mechanice teoretycznej, zasada najmniejszego wymuszenia (przymusu) lub zasada najmniejszej krzywizny. Dotyczy ona układu N punktów materialnych poddanych działaniu p więzów holonomicznych (więzy) i q więzów niecholonogicznych, spełniających ponadto założenia mówiące, że w chwili początkowej wszystkie ruchy mają to samo położenie i prędkości początkowe. Wówczas zasada Gaussa głosi, że dla ruchu rzeczywistego przymus G, przyjmuje najmniejsze wartości. W przypadku ruchu po gładkiej powierzchni ruch rzeczywisty odbywać się będzie wzdłuż krzywej o najmniejszej krzywiźnie. Można wykazać, że zasada Gaussa jest równoważna zasadzie d'Alemberta.

Krzywizna - miara stopnia odchylenia danej figury geometrycznej od wzorca,

1. dla krzywej krzywizna n jest definiowana jako: n = dt/ds,

t - jednostkowy wektor styczny w danym punkcie do krzywej, a s jest elementem łuku tej krzywej.

2. dla powierzchni krzywizna K (tzw. krzywizna Gaussa) wyraża się wzorem K = 1(r1r2), r1 i r2 - tzw. promienie krzywizny w dwóch wzajemnie prostopadłych kierunkach, wzdłuż, których krzywizna przyjmuje wartości ekstremalne.

3. dla przestrzeni krzywizna dana jest ogólnym wyrażeniem tensorowym określonym poprzez pochodne tensora metrycznego gil i symbole Christoffela, definiuje się też tzw. krzywiznę skalarną.

Wspólnie z Weberem badał magnetyzm ziemski w specjalnie do tego celu zbudowanym obserwatorium. Inny niemiecki astronom i geodeta F.W.Bessel (1784-1846) jako pierwszy - na podstawie wszystkich dostępnych wówczas materiałów - wyznaczył (dokładną) wartość spłaszczenia Ziemi na podstawie jego obliczeń współrzędnych na elipsoidzie.

Praca Alberta Einsteina największego fizyka czasów nowożytnych, urodzonego w Niemczech, jego teoria względności stanowi podstawę zrozumienia praw natury i takich pojęć jak przestrzeń, czas, masa i energia. Teoria uznana jako teoria względności jest przede wszystkim teorią grawitacji.

Do rozwoju geodezji poprzez rozwój innych dziedzin nauki przyczyniło się również wiele innych znakomitych umysłów końca XVII i całego XIX w. takich jak:

• L.Euler (1707-1783) - znakomity szwajcarski matematyk, astronom i fizyk. Zajmował się wykorzystaniem pomiarów Księżyca do wyznaczenia figury Ziemi.

• J.L.Lagrangea (1736-1813) w swoich pracach poświęconych mechanice teoretycznej opisał metody związane z mechaniką nieba, wykorzystywane w geodezji satelitarnej, i który walnie przyczynił się do wprowadzenia systemu metrycznego.

• H.Cavendisha wyznaczył masy ziemi i wartość stałej powszechnej grawitacji (1798).

• J.C.Makswell - pracował nad falami elektromagnetycznymi.

• A.Fizean - jako pierwszy wyznaczył prędkość światła (1849).

• G.G.Coriolis - przedstawił teorię ruchu względnego.

• G.G Stokes (1819-1903) przedstawił w roku 1863 swoją teorie figury Ziemi w postaci rozwiązania problemu granicznego w geoidzie.

• H.Poincare (1854-1912) francuski matematyk fizyk i filozof rozwinął teorię ziemskich pływów. Zajmował się problemami geodezji fizycznej.

• F.R.Helmert (1843-1917) wszechstronny niemiecki geodeta i geofizyk pozostawił naukową spuściznę prawie we wszystkich działach geodezji. Wykorzystał postulat minimum sumy kwadratów anomalii grawimetrycznych sformułowany dla elipsoidy ziemskiej przez wybitnego polskiego geofizyka M.P.Rudzkiego (1862-1916).

• Węgierski geofizyk R.Eőtvős (1848-1919) położył zasługi w badaniach i pomiarach grawimetrycznych.

• Holender F.A.Vening-Meinesz (1887-1966) wniósł poważny wkład w rozwój teorii izostazji, a także dał praktyczne podstawy wyznaczania odchyleń pionu wywiedzionych z teorii Stokesa (1928).

• Włoscy geodeci P.Pizzetti (1910) i C.Somigliana (1926) rozwinęli teorię normalnego pola siły ciężkości stosowaną w geodezji po dzień dzisiejszy.

Ważne są również słowa M.S.Mołdeńskiego, współczesnego rosyjskiego geodetę, który w latach sześćdziesiątych naszego stulecia rozwinął nowe podejście do geodezji fizycznej, przedstawiając rozwiązanie zagadnienia granicznego geodezji na fizycznej powierzchni Ziemi.

Ważne są również słowa Leonharda Eulera, które napisał prezentując Francuskiej Akademii Nauk swoją metodę wykorzystania pomiarów Księżyca do wyznaczenia figury Ziemi ponad 200 lat temu. W wolnym przekładzie sens tych słów wyraża się następująco:

„...gdyby Księżyc znajdował się bliżej Ziemi albo gdybyśmy mieli w pobliżu

Ziemi inne ciała niebieskie, które można byłoby obserwować, to moja metoda wyznaczania figury Ziemi byłaby bardziej przydatna niż pomiary stopnia i triangulacja”

13

Mikołaj Kopernik

Arystoteles

---