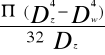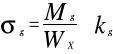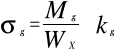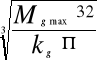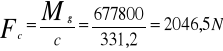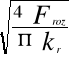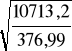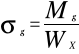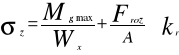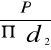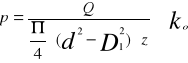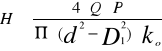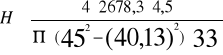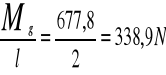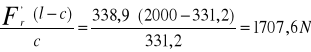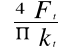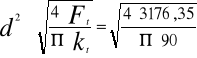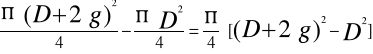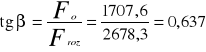Politechnika

Projekt nr 1

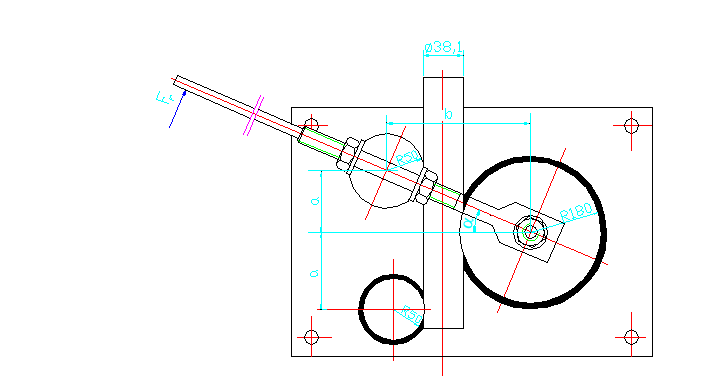
Temat:Zginarka do rur 1,5"

Dane: Obciążenie -rura 1,5″

Promień gięcia -100÷200mm

Typ produkcji - jednostkowa

Wykonał: Prowadzący :

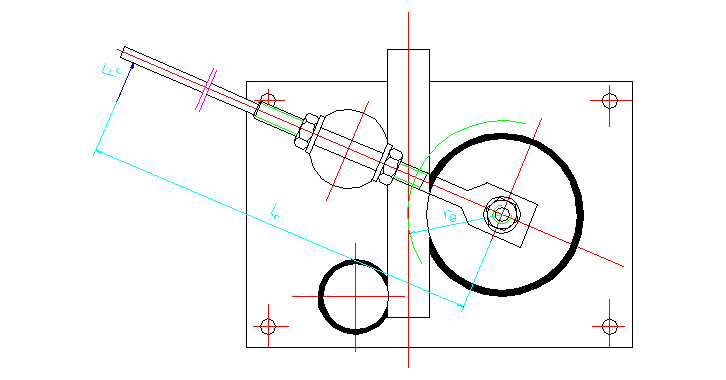
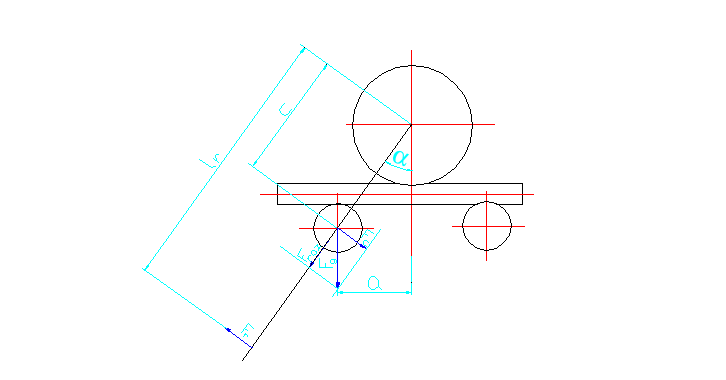
Rys.1.Szkic zginarki do rur

Dane:	Obliczenia:	Wyniki:
kg=145MPa kr=120MPa Dz=1,5" 1,5"=38,1mm Dz=38,1mm kg=145MPa Wx=4674,25 mm^3 l r=2 m Fr=350 N Mg≈677,8Nm kg=145MPa Mgmax=700 Nm kr=120MPa Dz=38,1 mm a=200 mm rk=50 mm rkr=50 mm Rk=180 mm	1.Ogólne założenia -przyjmuję materiał na dźwignię stal St3S , dla której kg,kr [3] -aby rurę zgiąć musi być spełniony następujący warunek : rg≥5∙Dz rg≥190,5mm przyjmuję promień gięcia rg=200mm -rury stalowe bez szwu walcowane na gorąco wg PN-80/H-74219 dla Dz=38,1mm grubość ścianki wynosi 2,6÷7,1mm, dalsze obliczenia przeprowadzam dla rur o grubości ścianki 7,1mm gdyż do wygięcia takiej rury jest potrzebny największy moment gnący -na rury stosuje się stal St3S [1] 2.Obliczam wartość momentu gnącego jaki musi być zrealizowany , aby rura została wygięta. -obliczam wartość wskaźnika wytrzymałości przekroju rury na zginanie Wx= Dw=Dz−2∙g Dw=38,1−2∙7,1 Dw=23,9mm Wx=4674,25mm^3 - z warunku wytrzymałościowego na zginanie (zmieniając w nim znak na przeciwny ) obliczam wartość momentu gnącego jaki jest potrzebny do zgięcia rury , Mg≤kg∙Wx czyli otrzymuję : Mg>kg∙Wx Mg>145∙4674,25 Mg>677766,25 Nmm ≈ 677,8 Nm -przyjmuję długość ramienia l r=2m i siłę przyłożoną do ramienia Fr=350N maksymalny moment gnący realizowany na zginarce wynosi : Mgmax=l r∙ Fr=700 Nm zatem : Mgmax>Mg 700>677,8 czyli nastąpi wygięcie rury, 3.Obliczam średnicę dźwigni : - z warunku wytrzymałościowego na zginanie Wx= Mgmax≤ po przekształceniu otrzymuje d≥ d≥36,64 mm z warunku wytrzymałościowego na rozciąganie = ≤kr 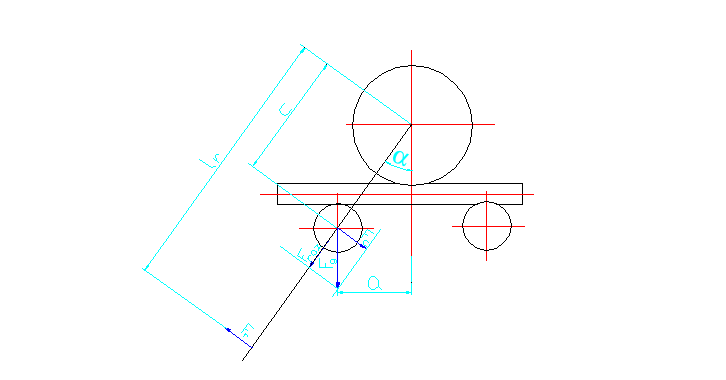A= -geometryczne warunki pracy zginarki : a=200 mm rk=50 mm rkr=50 mm Rk=180 mm b=Rk+Dz+rkr-4,1=180+38,1+50-4,1=264 mm b=264 mm -korzystając z funkcji trygonometrycznych obliczam wartość kąta α tgα = tgα = =0,76 arctg 0,76 = α α=37,23º	Dw=23,9mm Wx=4674,25 mm^3 Mg=677,8Nm d≥36,64mm b=264 mm α=37,23º

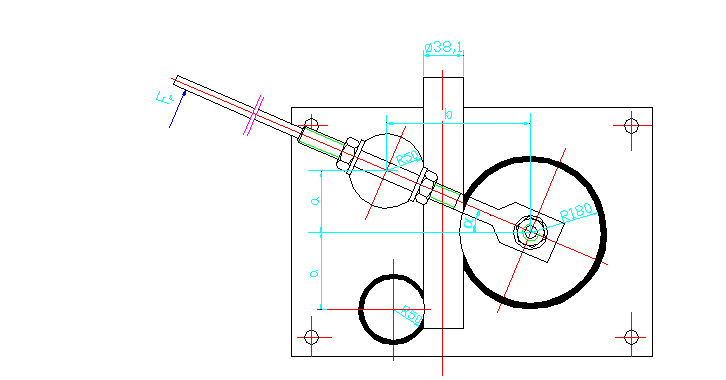
Rys.2. Szkic obrazujący geometryczne warunki pracy zginarki

a=200 mm b=264 mm

c^2=a^2+b^2 c= = = =331,2 mm

c=331,2 mm

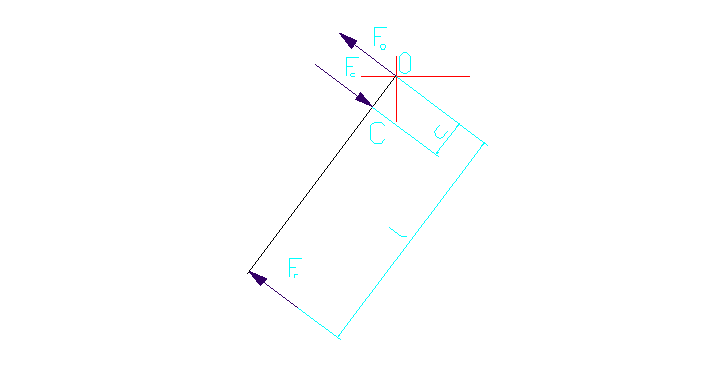
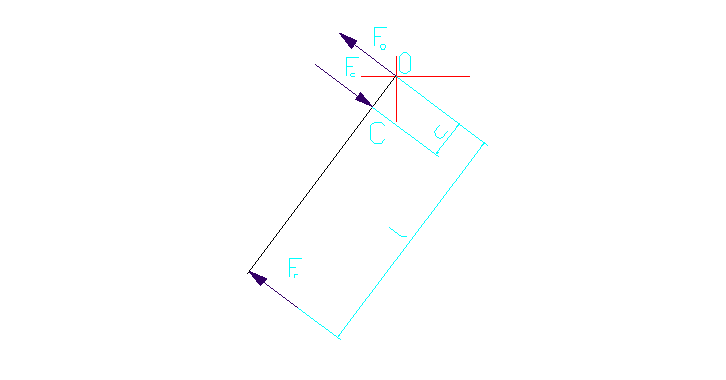
Rys.3.Rozkład sił działających na dźwignię

Mg=677,8 Nm c=331,2mm				- z własności dźwigni jednoramiennej (w stanie równowagi suma algebraiczna momentów sił działających na dźwignię względem punktu jej obrotu równa się zeru ) obliczam wartość siły działającej na dźwignię w miejscu styku z rurą Mg-Fc·c=0 Mg=Fc·c
α=37,23º kr=120 MPa Froz=2678,3N d=40 mm Mgmax=700Nm Froz=2678,3N kr=120MPa P=4,5 mm d2=42,08 mm α=60º μ=0,17 d=45 mm D1=40,13 mm kc=110MPa P=4,5 mm Froz=2678,3N			- znając wartość siły Fc i kąta α wyznaczam wartość siły rozciągającej działającej na dźwignię tgα= po przekształceniu otrzymuje Froz= Froz= N po obliczeniu siły rozciągającej podstawiam do warunku wytrzymałościowego na rozciąganie = ≤kr A= po podstawieniu za A i przekształceniu wzór przyjmuje następującą postać d≥ d≥ d≥ d≥5,33 mm na podstawie otrzymanych wyników z warunków wytrzymałościo- wych na zginanie i rozciąganie średnica dźwigni musi być większa od 36,64 mm ,przyjmuję d=40 mm 4.Sprawdzam wytrzymałość dźwigni na naprężenia złożone korzystając z hipotezy Hubera σz= ≤kr w rozważanym przypadku dźwignia pracuje tylko na rozciąganie i zginanie , zatem τ=0 wzór przyjmuje postać σz=σg+σr≤kr = Wx= A= =1256,64mm^2 Wx= =6283,18 mm^3 po podstawieniu do wzoru otrzymujemy MPa ≤120 MPa Dobieram gwint M45 , dla którego według PN-83/M-02013 [1]: D1=d3=40,13 mm D2=d2=42,08 mm P=4,5 mm D=d=45 mm α=60º 5.Sprawdzam samohamowność gwintu z warunku : ρ^'>γ ρ^'-pozorny kąt tarcia γ-wznios gwintu równy wzniosowi linii śrubowej obliczam kąt pochylenia linii śrubowej tgγ= = =0,034 arc tg 0,034=γ γ=1,95º -obliczam wielkość pozornego kąta tarcia pomiędzy nakrętką a śrubą μ'=tg ρ'= μ'-pozorny współczynnik tarcia ρ'-pozorny kąt tarcia αr - kąt roboczy gwintu , dla gwintów o zarysach symetrycznych αr=0,5∙α=30º μ,ρ -w gwintach płaskich - przyjmuję materiał na nakrętkę St3 dla której kr=110 MPa μ- współczynnik tarcia pomiędzy nakrętką a śrubą μ=0,15÷0,17 - stal po stali na sucho w spoczynku [2] do wzoru na pozorny współczynnik tarcia podstawiam μ=0,17 μ'=tg ρ'= = =0,196 arc tg 0,196 = ρ' ρ'=11,09º ρ^'>γ 11,09º>1,95º warunek został spełniony , gwint jest samohamowny 6.Obliczam wysokość nakrętki z warunku wytrzymałościowego na naciski powierzchniowe [4] Q-siła osiowa obciążająca złącze gwintowe H-czynna wysokość nakrętki ko=0,3∙kc - w połączeniach spoczynkowych dokręcanych tylko przy montażu z-liczba czynnych zwojów gwintu Q=Froz=2678,3N materiał na nakrętkę stal St2 kc=110MPa -dla stali St2 [3] zatem ko=0,3∙110 =33 MPa po podstawieniu za z i przekształceniu , otrzymujemy: H≥1,12 mm zalecana liczba czynnych zwojów z=(6÷10) ze względu na dobre prowadzenie śruby w nakrętce przyjmuję z=6 zatem wysokość nakrętki wynosi H=z∙P=6∙4,5=27 mm 7.Obliczam średnicę elementu , na którym będzie osadzona dźwignia z warunku wytrzymałościowego na ścinanie ≤kt n-liczba ścinanych przekrojów (n=1) przyjmuję materiał na kołek stal St6, dla której kt=105MPa [3] -obliczam wartość siły tnącej działającej na kołek					Fc=2046,5 N Froz=2678,3N d≥5,33 mm A=1256,64 mm^2 Wx=6283,18 mm^3 μ'=0,196 ρ'=11,09º Q=2678,3N ko=33MPa H=27 mm
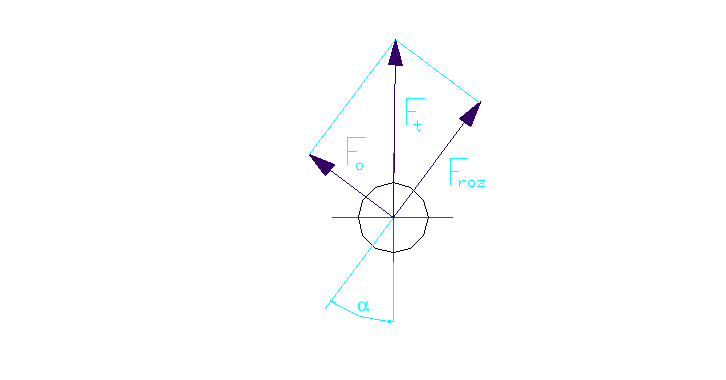
Rys.4.Szkic obrazujący siły działające na dźwignię w stanie równowagi
Mg=677,8Nm l=2m Fc=2046,5N c=331,2mm		Fr'-wartość siły wywieranej na dźwignię , przy której jeszcze nie następuje zginanie rury Mg= Fr'∙l Fr'= ∑Mic= − Fr'∙ (l−c)+Fo∙c=0 po przekształceniu otrzymuje Fo=					Fr'=338,9N Fo=1707,6N
Rys.5.Rozkład sił tnących działających na kołek
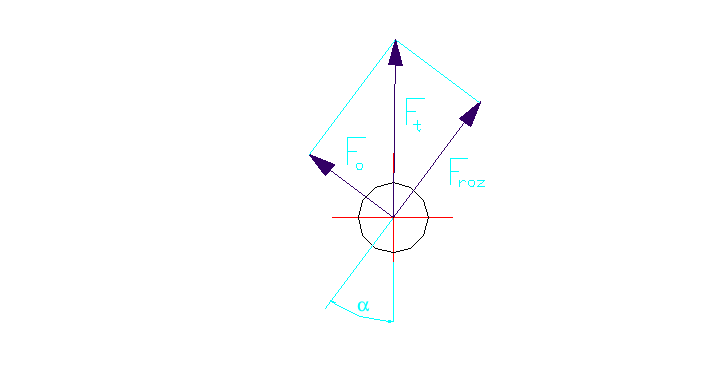
Froz=2678,3N Fo=1707,6N n=1 kt=105MPa Ft=3176,35N		Ft^2=Fo^2+Froz^2 Ft= znając wartość siły tnącej działającej na kołek podstawiam ją do warunku wytrzymałościowego na ścinanie A= po podstawieniu za A , n i przekształceniu otrzymujemy : d^2				Ft=3176,35N
d1=10 mm d2=14 mm l1=25 mm l2=50 mm Rk=180 mm Ft=3176,35N Fo=1707,6N Froz=2678,3N α=60º	d≥6,2 mm ze względu na właściwe ustalenie dźwigni , przyjmuję wykonanie kołka jako elementu dwustopniowego , średnica dolnego stopnia d1=10 mm ,a górnego stopnia d2=14 mm długość dolnego stopnia l1=25 mm , który będzie osadzony w otworze wykonanym w krążku Rk przez wcisk H7/p6 wg PN-77/M-02105 [3] dla H7 ES=0,015 mm , EI=0 dla p6 es=0,024 ,ei=0,015 górny stopień o długości l2=50 mm będzie współpracował z otworem wykonanym w nasadzie dźwigni H7/h6 wg PN-77/M-02105 [3] dla H7 ES=0,018 mm , EI=0 Dla h6 es=0 , ei= - 0,011 mm na stopniu o średnicy d2 w odległości a=6,5 mm od powierzchni czo- łowej kołka będzie wykonany otwór o średnicy d=2 mm przechodzący przez oś kołka pod zawleczkę , która będzie tylko spełniała rolę elementu zabezpieczającego przed spadnięciem dźwigni i ustalała jej położenie zawleczka stalowa wg PN-76/M-82001 średnica zawleczki d0=2 mm a długość l=12÷25 mm przyjmuję l=20 mm zatem długość kołka wynosi : lk=l1+l2=25+50=75 mm 8.Obliczam grubość spoiny z warunku wytrzymałościowego na ścina -nie F-przekrój obliczeniowy spoiny pachwinowej g=0,7∙h F= D=2∙Rk=2∙180=360 mm kt krążki ze stali St2S , dla której kt=70 MPa [3] zatem 70=4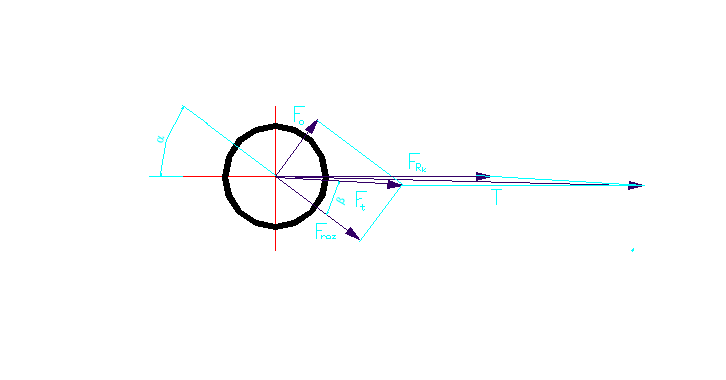5,5 MPa -obliczam siłę tnącą T działającą na spoinę korzystając z twierdzenia cosinusów T= -obliczam wartość kąta β arctg0,637=β							d≥6,2 mm l=20 mm d0=2 mm lk=75 mm D=360 mm kt=45,5 MPa

Rys.6.Rozkład sił tnących działających na spoinę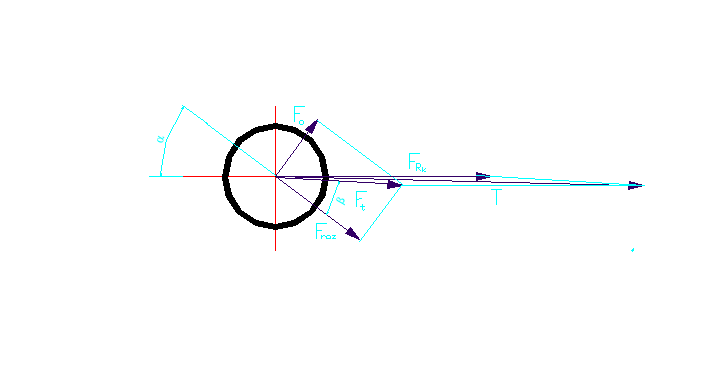

β=32,5º -obliczam siłę FRk przenoszoną przez spoinę

β=32,5º

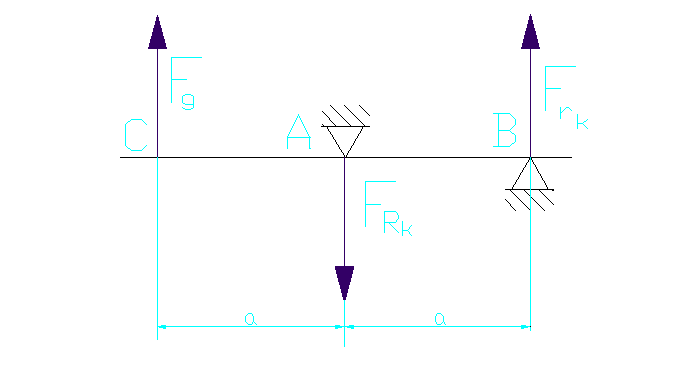
Rys.7.Rozkład sił działających na rurę
	Na podstawie rys.7 ∑MiA=0 ∑MiA=−Fg∙a+FRk∙a=0 po przekształceniu otrzymuję
Froz=2678,3N Fc=2046,5N Ft=3176,35N Frk=3370,67 N α=37,23º β=32,5º kt^,=45,5MPa T=9910,33N D=360 mm	FRk=Fg (patrz rys.3.) zatem: Frk=3370,67N ∑Fiy=Fg−FRk+Frk=0 FRk=Fg+Frk=3370,67+3370,67=6741,34N T= T= =9910,33N po przekształceniu otrzymuję F F F≥217,81mm^2 F= ≥217,81 po przekształceniu otrzymuję (D+2∙g)^2 g≥0,19 mm ze względu na trudność wykonania spoiny o tak małej grubości i znacznych wymiarów krążka przyjmuję g=2 mm g=0,7∙h h=3 mm dla krążka o promieniu rk=50 mm również g=2 mm , h=3 mm 9.Ustalenia końcowe płyta zginarki blacha stalowa St2S o grubości 3 mm wg PN-76/H-92201, o wymiarach 570x560 mm -w płycie na rogach wykonane są otwory ø12 mm pod śruby do mocowania zginarki ( otwory są rozmieszczone symetrycznie po rogach )	Fg=3370,67N Frk=3370,67 N FRk=6741,34 N T=9910,33N F≥217,81 mm^2 g≥0,19 mm h=3 mm

Literatura:

[1]W. Juchnikowski: Podstawy konstrukcji maszyn.WPW 1995 Warszawa

[2]M. Godlewski: Poradnik dla mechaników. WSiP 1991 Warszawa

[3]Praca zb. pod red. A.Rutkowskiego :Zbiór zadań z części maszyn.WSiP 1990 Warszawa

[4]A.Rutkowski:Części maszyn.WSiP 1992 Warszawa

5

11

---