ZASTOSOWANIA RACHUNKU RÓŻNICZKOWEGO
Pojęcie pochodnej funkcji jest podstawowym pojęciem analizy matematycznej i ma szerokie zastosowania. Definicję pochodnej podali niezależnie od siebie Newton, w związku z rozważaniami dotyczącymi prędkości ruchu punktu materialnego, oraz Leibniz, przy rozpatrywaniu zagadnienia stycznej do krzywej.
Kinematyczną (fizyczną) interpretacją pochodnej jest prędkość chwilowa w ruchu prostoliniowym.
Przypuśćmy, że ciało porusza się po linii prostej, przebywając pewną drogę od punktu początkowego O. Prędkość średnia tego ciała w odstępie czasu ![]()
wyliczmy z dobrze znanego nam wzoru
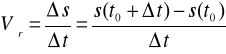
Ale jeśli byśmy chcieli znać dokładną wartość prędkości ciała w momencie t0 musielibyśmy liczyć ją, gdy przyrost czasu![]()
jest znikomy, tzn. gdy ![]()
, czyli
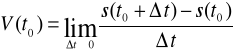
Oznacza to, że prędkość ciała w dowolnym momencie jest pochodną funkcji s(t), której wartość określa drogę przebytą w czasie t (zob. definicja pochodnej funkcji).
Definicja.
Niech dana będzie funkcja f : A→R, A⊂R. Jeżeli istnieje granica skończona
![]()
to granicę tę nazywamy pochodną funkcji f w punkcie x0 i oznaczamy najczęściej symbolem f '(x0).
Iloraz
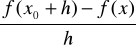
przyrostu wartości funkcji do przyrostu argumentu nazywamy ilorazem różnicowym funkcji.
Wzory na pochodne wybranych funkcji znajdują się w dołączonej tablicy.
I. Różne interptetacje pochodnej
1. Interpretacja geometryczna. Równanie stycznej
Jeżeli funkcja f jest ciągła w punkcie x0 i ma w tym punkcie pochodną f '(x0), to do wykresu tej funkcji istnieje w punkcie (x0, f(x0)) styczna o równaniu
y-f(x0)=f '(x0)(x- x0).
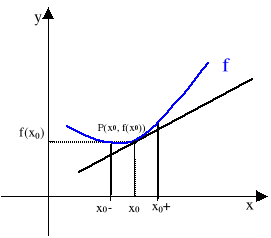
Styczna ta jest granicą siecznych przechodzących przez punkty A(x0, f(x0)) oraz
B(x0+h, f(x0+h)) przy h zmierzającym do 0. Fakt ten ilustruje poniższy rysunek.
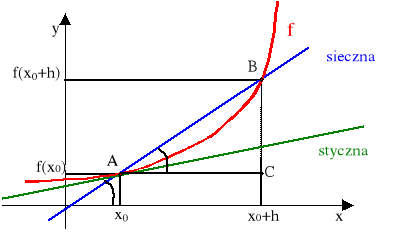
Długość odcinka BC jest równa przyrostowi wartości funkcji f odpowiadającego przyrostowi argumentu o h (długość odcinka AC). Iloraz różnicowy funkcji jest więc stosunkiem długości odcinków BC do AC. Jest on zatem równy tangensowi kąta α nachylenia siecznej AB do osi OX, co oznacza, że w sensie geometrycznym jest on równy współczynnikowi kierunkowemu siecznej AB.
Jeżeli przyrost argumentu h maleje do zera, to punkt B zbliża się do punktu A. Przy przejściu do granicy (czyli do pochodnej) punkt ten pokryje się z punktem A, a sieczna stanie się już styczną (im mniejszy przyrost argumentu h, tym bardziej sieczne zbliżają się do stycznej). Zatem pochodną w punkcie x0 możemy interpretować geometrycznie jako współczynnik kierunkowy stycznej do wykresu funkcji f w punkcie o współrzędnych (x0, f(x0)).
Przykład.
Wyznaczymy równanie stycznej do wykresu funkcji f(x)=3x2-5 w punkcie A(1,-2).
Zauważmy od razu, że x0=1 i f(x0)=f(1)=-2. Aby skorzystać z podanego wzoru stycznej, brakuje nam tylko wartości f'(1). W tym celu policzmy pochodną
f'(x)= 6x oraz f'(1)= 6∙1=6.
Na podstawie podanego wzoru stycznej otrzymujemy
y-(-2)=6(x-1)
czyli równane stycznej do funkcji w punkcie A(1,-2) ma postać
y=6x-8
2. Interpretacja ekonomiczna.
a) Prędkość zmian wartości funkcji .
Iloraz różnicowy
![]()
nazywamy też często przyrostem średnim albo przeciętnym funkcji f w przedziale [x0, x0+h] .
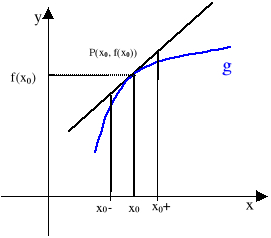
Określenie przyrost średni (przeciętny) oznacza przyrost przypadający średnio (przeciętnie) na jednostkę przyrostu zmiennej x na odcinku h. Iloraz różnicowy jest więc miarą średniej prędkości zmiany wartości funkcji f w przedziale [x0, x0+h] . Widać że zależy on zarówno od x0 jak i od h.
Przy ustalonym x0 przyrost średni można uważać za miarę reakcji (czułości) funkcji f na przyrost zmiennej liczonej od punktu x0. Gdy małym przyrostom argumentu h odpowiadają małe przyrosty wartości ilorazu różnicowego to mówimy, że funkcja nie jest czuła w danym punkcie x0 na przyrost zmiennej o h. W przeciwnym wypadku, gdy przyrost wartości ilorazu różnicowego jest znaczny, to o takiej funkcji będziemy mówić, że jest czuła.
Z dwóch funkcji których wykresy przedstawiono na rysunku, funkcja g jest bardziej czuła w punkcie x0 na przyrost h niż funkcja f.
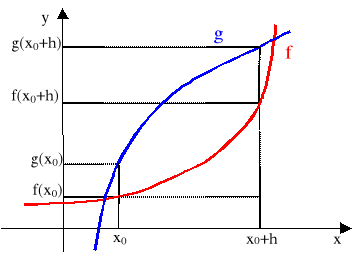
Przechodząc w ilorazie różnicowym do granicy przy h→0, uzyskujemy oczywiście pochodną funkcji f w punkcie x0. Jest ona miarą prędkości zmian wartości funkcji w otoczeniu punktu x0 niezależną od wartości przyrostu h.
b) Funkcja kosztów
Niech K(x) oznacza funkcje kosztów, tzn. oznacza koszt całkowity wyprodukowania x jednostek pewnego produktu. Wtedy iloraz różnicowy tej funkcji oznacza koszt przeciętny wytworzenia jednostki produktu, przy zwiększeniu produkcji od x0 do x0+h. Natomiast iloraz
![]()
jest kosztem przeciętnym przypadającym na jednostkę produkcji.
Jeżeli funkcja K(x) posiada pochodną, to funkcję K'(x) nazywamy funkcją kosztów krańcowych.
Pochodna K'(x0) funkcji kosztów K(x) w punkcie x0 nazywamy kosztami krańcowymi w punkcie x0. Pochodną tę interpretujemy jako prędkość zmian kosztów przy poziomie produkcji x0.
Ponieważ
K (x0+h)- K (x0) ≈ K'(x0)∙h,
to w szczególności przyjmując h=1 mamy
K (x0+1)- K (x0) ≈ K'(x0)∙
co oznacza, że podniesienie produkcji o jedną jednostkę powoduje zwiększenie kosztów produkcji o K'(x0). Koszty krańcowe w punkcie x0 są zatem równe w przybliżeniu wartości nakładów zużytych na wyprodukowanie dodatkowej jednostki produktu w stosunku do poziomu wyjściowego x0.
Przykład.
Koszt całkowity wytworzenia x jednostek pewnego produktu określony jest wzorem
K(x)=2500+50x-0,01x3.
Wtedy funkcja kosztów krańcowych ma postać
K'(x)= 50-0,03x2.
Przy wysokości produkcji x=10 koszt krańcowy wynosi K'(10)= 50-0,03∙100= 47 jednostek pieniężnych, natomiast przy x=20 koszt ten jest równy K'(x)= 50-0,03∙400=38 jednostek pieniężnych.
Tak więc przybliżony koszt wyprodukowania dodatkowej jednostki przy poziomie produkcji x=10 wynosi K'(10)= 47, a przy poziomie produkcji x=20 wynosi K'(20)= 38.
Można to zinterpretować, że produkcja 20 jednostek jest korzystniejsza niż 10 jednostek.
3. Elastyczność funkcji
Jeżeli mamy daną funkcję f określoną dla x>0, przyjmującą tylko dodatnie wartości i różniczkowalną w dziedzinie, to liczbę określoną wzorem
![]()
nazywamy elastycznością funkcji f w punkcie x i oznaczamy symbolem Exf.
Elastyczność funkcji f w punkcie x jest przybliżoną miarą procentowego przyrostu (wzrostu lub spadku) wartości funkcji odpowiadającemu przyrostowi argumentu x o 1%. Przy przyjętych założeniach x0>0 i f(x0)>0, czyli znak elastyczności zależy tylko od znaku pochodnej f'(x0). Stąd, elastyczność funkcji rosnącej w otoczeniu x0 jest dodatnia w punkcie x0, natomiast elastyczność funkcji malejącej w otoczeniu x0 jest ujemna.
Przykład.
Ustalono, Ze pomiędzy popytem y na pewne dobro a przeciętnymi dochodami miesięcznymi x ludności istnieje zależność funkcyjna
![]()
Obliczmy elastyczność dochodową na dane dobro. Łatwo sprawdzić, że
![]()
Elastyczność dochodowa popytu na dane dobro wynosi więc
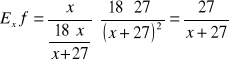
Jeżeli np. x=3, to E3f = 27/30 =0,9. Zatem przy dochodzie miesięcznym równym 3 (np. 3 tysiące złotych) wzrost dochodu o 1% pociąga za sobą wzrost popytu na dane dobro o 0,9%.
II. Monotoniczność funkcji
Jednym z najważniejszych zastosowań pochodnej funkcji jest badanie i wyznaczanie monotoniczności funkcji oraz wyznaczanie jej największej i najmniejszej wartości (w całej dziedzinie, lub jej podzbiorze). Badanie monotoniczności funkcji za pomocą pochodnych opiera się na następującym twierdzeniu Lagrange'a.
TWIERDZENIE Lagrange'a
Jeżeli funkcja f jest ciągła w przedziale domkniętym [a, b] i różniczkowalna wewnątrz tego przedziału, to istnieje taki punkt c∊(a, b), że
![]()
Wartość f'(c) interpretujemy jako średnią szybkość zmian wartości f(x) w przedziale [a, b]. Dlatego też twierdzenie to nosi nazwę twierdzenia o wartości średniej, lub twierdzenia o przyrostach.
Wnioski z tego twierdzenia są następujące:
1. Jeżeli pochodna funkcji f jest równa zero w każdym punkcie przedziału (a, b) to funkcja f jest stała w tym przedziale.
2. Jeżeli pochodna funkcji f jest dodatnia w każdym punkcie przedziału (a, b) to funkcja f jest w tym przedziale rosnąca.
3. Jeżeli pochodna funkcji f jest ujemna w każdym punkcie przedziału (a, b) to funkcja f jest w tym przedziale malejąca.
Przykład.
Zbadamy monotoniczność funkcji f(x) = 4+3x2-x3.
Funkcja ta jako funkcja wielomianowa jest różniczkowalna. Policzmy jej pochodną i zbadajmy jej znak.
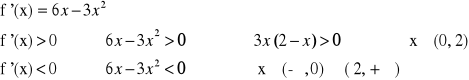
Zatem funkcja rośnie w przedziale (0, 2), natomiast maleje w przedziałach (-∞, 0) i (2,∞).
III. Ekstrema lokalne funkcji
Drugim bardzo ważnym zastosowaniem pochodnej funkcji jest wyznaczanie ekstremów lokalnych funkcji. Ekstremami lokalnymi funkcji nazywamy maksima i minima lokalne funkcji.
Mówimy, że funkcja f ma w punkcie x0 maksimum (minimum) lokalne równe f(x0), jeżeli istnieje takie otoczenie (x0-δ, x0+δ) punktu x0, że dla każdego x∊(x0-δ, x0+δ) zachodzi nierówność
f(x)≤ f(x0) ( f(x)≥ f(x0) )
Powyższe określenia ilustrują rysunki.
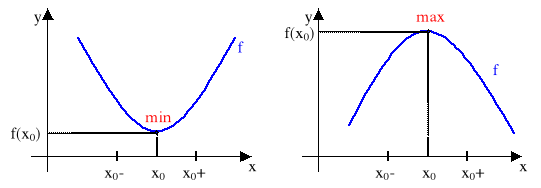
Pojęcie ekstremum funkcji w punkcie jest pojęciem lokalnym odnoszącym się do małego otoczenia tego punktu i nie należy go mylić z wartością najmniejszą i największą funkcji!
Pojęcia wartość największa lub wartość najmniejsza są globalne, a więc odnoszące się do całego zbioru, w którym określona jest dana funkcja.
Funkcja f może mieć w przedziale określoności kilka minimów i maksimów lokalnych, ale tylko jedną wartość najmniejszą i największą, która nie koniecznie musi być ekstremum lokalnym.
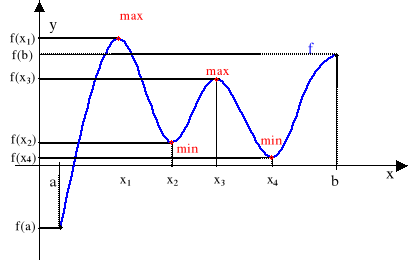
Na przedstawionym rysunku funkcja f w punktach x1 i x3 ma maksimum lokalne, a w punktach x2 i x4 minimum lokalne. Jednocześnie zauważmy, że najmniejszą wartością tej funkcji w przedziale [a, b] jest f(a), a największą f(x1). Tak więc w przedziale [a, b] funkcja f osiąga w punkcie x=a minimum globalne (mimo, że nie jest to minimum lokalne!), a w punkcie x=x1 maksimum globalne.
Ponieważ bezpośrednio z definicji trudno jest wyznaczyć ekstremum, sformułujemy teraz twierdzenia podające warunki konieczne i wystarczające istnienia ekstremum lokalnego funkcji f w punkcie x0.
TWIERDZENIE Fermata
Jeżeli funkcja różniczkowalna f ma w punkcie x0 ekstremum, to f '(x0)=0.
Twierdzenie Fermata orzeka, że warunkiem koniecznym na to, aby funkcja f różniczkowalna w punkcie x0, miała w tym punkcie ekstremum jest zerowanie się pochodnej w tym punkcie.
Zerowanie się pochodnej w pewnym punkcie nie wystarcza jednak do istnienia ekstremum, w tym punkcie czego dowodem jest poniższy przykład.
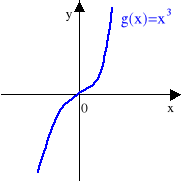
Przykład 1.
Funkcja g(x)=x3 nie ma ekstremum w punkcie x0=0 (co jest widoczne na poniższym rysunku), ale jak łatwo sprawdzić g'(0)=0.
Pojawia się wiec pytanie o warunek wystarczający istnienia ekstremum i określenia jego typu (czy jest to maksimum czy minimum). Odpowiedź jest następująca.
Warunkiem wystarczającym na to, aby funkcja f miała w punkcie x0, w którym pochodna się zeruje (f'(x0)=0) ekstremum jest zmiana znaku pochodnej w tym punkcie, przy czym jeśli pochodna zmienia znak z - na +, to funkcja ma w punkcie x0 minimum, natomiast jeśli pochodna zmienia znak z + na -, to funkcja ma w punkcie x0 maksimum.
Przykład 2.
Zbadajmy ekstrema funkcji f(x)=2x3+3x2-36x+15.
Obliczamy pochodną:
f'(x) = 6x2+6x-36
f'(x) = 6 (x2+x-6),
czyli
f'(x) = 0 wtedy i tylko wtedy gdy x2+x-6 = 0, tj. dla x=-3 i x=2
Badamy teraz znak pochodnej. W tym celu narysujmy jej przybliżony wykres.
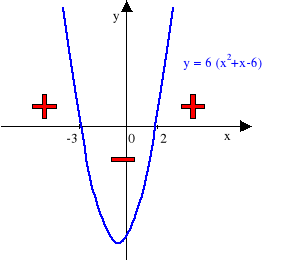
Widzimy więc, że w punkcie x=-3 funkcja ma maksimum (znak pochodnej zmienia się z + na - ) równe fmax(-3)=96, a punkcie x=2 funkcja ma minimum (znak pochodnej zmienia się z - na + ) równe fmin(2)=-19.
Przykład 3.
Zbadajmy jaką najmniejszą i jaką największą wartość przyjmuje funkcja
y = x3-3x2-9x+7 w przedziale [-2,1].
Wyznaczmy najpierw ekstrema lokalne tej funkcji. w tym celu policzmy pochodną
f'(x) = 3x2-6x-9
f'(x) =0 ⇔ 3(x+1)(x-3) = 0 ⇔ x=-1 lub x=3
Liczba 3 nas nie interesuje, gdyż leży poza przedziałem [-2,1]. Natomiast w punkcie x=-1 pochodna zmienia znak z + na -, czyli mamy maksimum lokalne równe fmax(-1)=12.
Aby wyznaczyć ekstremum globalne (wartość największą i najmniejszą) obliczamy ponadto wartośc funkcji w punktach -2 i 1.
f(-2)=5
f(1)=-4
Wartością największą funkcji f w przedziale [-2,1] jest największa spośród liczb: 12,5,-4, czyli 12. Natomiast wartością najmniejszą funkcji f w przedziale [-2,1] jest najmniejsza spośród tych liczb, czyli -4.
IV. Wklęsłość i wypukłość wykresu funkcji.
Wykres funkcji różniczkowalnej w punkcie x0 nazywamy wypukłym (wklęsłym) w tym punkcie, jeżeli istnieje takie otoczenie punktu x0, że dla każdego punktu x z tego otoczenia (oprócz niego samego) punkty P(x, f(x)) wykresu leżą powyżej (poniżej) stycznej poprowadzonej do wykresu w punkcie o odciętej x0.
Wykres funkcji wypukły (wklęsły) w każdym punkcie przedziału (a, b) nazywamy wypukłym (wklęsłym) w tym przedziale.
Przykładem funkcji, która ma wykres wypukły jest funkcja f , natomiast o wykresie wklęsłym funkcja g.
Jeżeli w pewnym punkcie x0 wykres funkcji f zmienia się z wypukłego na wklęsły lub odwrotnie, to punkt P(x0, f(x0)) nazywamy punktem przegięcia krzywej y=f(x).
Okazuje się, że przy pomocy pochodnych można w łatwy sposób badać wypukłość krzywych oraz wyznaczać ich punkty przegięcia. Zachodzą mianowicie następujące twierdzenia:
TWIEWDZENIE 1. Jeżeli druga pochodna funkcji f jest dodatnia w każdym punkcie przedziału (a, b), to wykres funkcji f jest w tym przedziale wypukły.
TWIERDZENIE 2. Jeżeli druga pochodna funkcji f jest ujemna w każdym punkcie przedziału (a, b), to wykres funkcji f jest w tym przedziale wklęsły.
TWIERDZENIE 3. Jeżeli druga pochodna funkcji f spełnia warunki:
f''(x0)=0
w otoczeniu punktu x0 ma po obu stronach tego punktu różne znaki,
to punkt P(x0, f(x0)) jest punktem przegięcia wykresu funkcji f.
Przykład.
Zbadamy wypukłość i wyznaczymy punkty przegięcia wykresu funkcji f(x) = 2x3+3x2-4x+10.
Policzmy pochodne (pierwszą i drugą):
f'(x) = 6x2+6x-4 f''(x) = 12x+6 = 6 (2x+1)
i narysujmy przybliżony wykres pochodnej
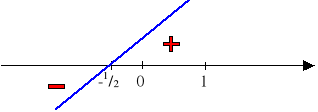
Widzimy zatem, że wykres funkcji f jest wypukły w przedziale (-1/2, +∞) (druga pochodna funkcji f jest dodatnia), natomiast w przedziale (-∞,-1/2) wklęsły (druga pochodna funkcji f jest ujemna).
Ponieważ w punkcie x0=-1/2 druga pochodna zeruje się i zmienia w otoczeniu tego punkty znak, to punkt x0=-1/2 jest punktem przegięcia wykresy tej funkcji.
Zadania do samodzielnej realizacji
Zad.1 Wyznaczyć równanie stycznej do wykresu funkcji
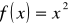
w punkcie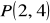
,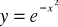
w punkcie o odciętej równej 1;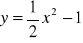
równoległej do prostej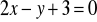
.
Zad.2 Dane są funkcje
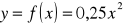
;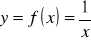
;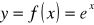
.
Dla każdej funkcji f wyznaczyć jej elastyczność.
Zad.3 Wyznaczyć przedziały monotoniczności funkcji
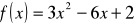
;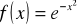
;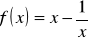
;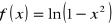
;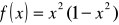
.
Zad. 4 Wyznaczyć ekstrema lokalne funkcji
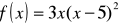
;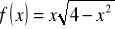
;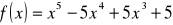
;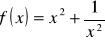
;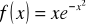
.
Zad. 5 Wyznaczyć najmniejszą i największą wartość funkcji w danym przedziale
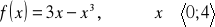
;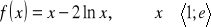
;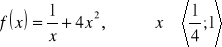
.
Zad. 6 Wyznaczyć przedziały wypukłości i punkty przegięcia wykresu funkcji
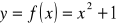
;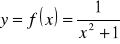
;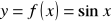
;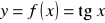
;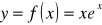
.
Zad.7 Z prostokątnego kawałka blachy o szerokości 80 cm i długości 120 cm robi się opakowanie w ten sposób, że w rogach wycina się kwadraty, następnie zagina wystające brzegi i lutuje na krawędziach. Zbadać, jak wielkie należy wyciąć kwadraty, aby otrzymać opakowanie o możliwie największej pojemności.
Zad.8 Jaki powinien być stosunek wymiarów puszki do konserw w kształcie walca, aby przy danej objętości zużyć na jej wyrób jak najmniej blachy ?
Zad.9 Wartość produkcji zakładu kształtuje się według funkcji ![]()
zł za x roboczogodzin. Znaleźć wydajność krańcową przy zatrudnieniu 5-ciu robotników.
Wzory na pochodne podstawowych funkcji
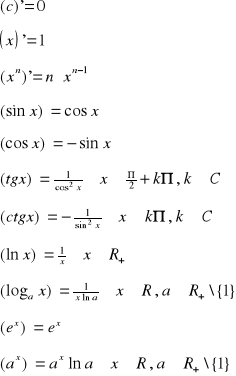
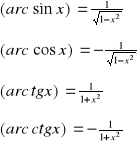
Wyszukiwarka
Podobne podstrony:
CALY E -TRAPEZ, PWR, Analiza Matematczna
Pochodnesciagi, studia, Matma, Analiza Matematyczna, analiza, Ściągi
Zastosowania całki oznaczonej w geometrii, Analiza matematyczna
Pochodna i ekstrema funkcji, Analiza matematyczna
Zadanie domowe - pochodne, ZiIP, Semestr I, Analiza matematyczna, Zadanie z pochodnych
wejściówki pytania, Inżynieria materiałowa pwr, Analiza instrumentalna laborki
CALY E -TRAPEZ, PWR, Analiza Matematczna
Pochodna funkcji 3, PWR, semestr I, analiza matematyczna, materiały do nauki od DOROTY
POCHODNE I ICH ZASTOSOWANIA, ZiIP, Semestr I, Analiza matematyczna
Analiza matematyczna, lista analiza 2008 10 zastosowania pochodnych
Wybrane zastosowania pochodnej funkcji, Analiza matematyczna
przykładowe pochodne, PWR, semestr I, analiza matematyczna
El-ka lista 1, PWR, semestr I, analiza matematyczna, materiały do nauli matmy fizyki itp
Analiza matematyczna lista analiza 2008 10 zastosowania pochodnych
Granica ciągu 1, PWR, semestr I, analiza matematyczna, materiały do nauki od DOROTY
więcej podobnych podstron