Dla układów mechanicznych pokazanych na rysunkach w tablicy 6 podać równania równowagi statycznej, a następnie rozwiązać te równania tak, aby określić siły reakcji więzów.

1) Dane: P [N] G[N] a [m] b [m] c [m] d [m] 1 - pręt o ciężarze G 2..6-pręty, których ciężary własne pomijamy	2) Dane: Q [N] P [N] G [N] a [m] b [m] c [m] 1 - pręt o ciężarze G 2..6-pręty, których ciężary własne pomijamy
3) Dane: P [N] G [N] a [m] b [m] c [m] 1..6 - pręty, których ciężary własne pomijamy 7 - płyta jednorodna o ciężarze G	4) Dane: P [N] G [N] a [m] b [m] c [m] d [m] 1..6 - pręty, których ciężary własne pomijamy 7 - płyta jednorodna o ciężarze G
5) Dane: M= Pa [Nm] P1=P [N] Q [N] a [m] sześcian o boku a 1-pręt o ciężarze P1 2-6-pręty, których ciężary pomijamy	6) Dane: Q [N] P [N] M=Pa [Nm] a [m] sześcian o boku a 1-pręt, którego ciężar własny pomijamy 2- jednorodna płyta płaska o ciężarze P
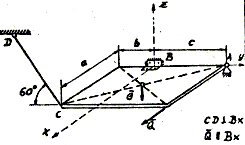
7) Dane: G [N] Q [N] a [m] b [m] G - ciężar jednorodnej płyty płaskiej, CD - pręt, którego ciężar własny pomijamy	8) Dane: G [N] Q [N] a [m] b [m] c [m] G - ciężar jednorodnej płyty płaskiej, CD - pręt, którego ciężar własny pomijamy

Tablica 6. Przykłady równowagi przestrzennych dowolnych układów sił

1

C

A

2

1

D

B

M

2

3

6

5

4

1

D

E

C

B

A

G

F

H

5

c

b

a

E

B

D

A

3

6

2

7

4

1

C

E

J

G

F

H

5

c

b

a

C

D

A

3

6

2

7

4

1

B

d

d

c

b

a

C

E

D

A

B

3

6

2

5

4

1

F

c

a

b

E

B

A

C

D

5

4

6

3

2

1

---