I.29

W zamkniętym zbiorniku o zasobie objętości V=25m³ znajduje się powietrze traktowane tak jak gaz doskonały o ciśnieniu p₁=0,1[MPa] i temperaturze t₁=13 [ºC]. Na skutek doprowadzenia w przemianie izochorycznej odwracalnej ∆Q ilości ciepła ciśnienie w zbiorniku wzrosło do p₂=0,235[MPa]. Obliczyć ilość ciepła ∆Q doprowadzonego do układu oraz przyrosty zasobów entalpii ∆H i entropii ∆S jeżeli wykładnik izentropy k=1,4

Dane: Obliczyć:

V=25 [m³] ∆Q=?

p₁=0,1 [MPa] ∆H=?

t₁=13 [ºC] ∆S=?

p₂=0,235 [MPa]

k=1,4

1. Wykres sprężania powietrza w przemianie izochorycznej odwracalnej we współrzędnych p(V)

2. Wyznaczenie z równania stanu gazu doskonałego Clapeyrona zasobu masy powietrza w zbiorniku

3. Wyznaczenie ciepła właściwego przy stałym ciśnieniu i objętości w funkcji indywidualnej stałej gazowej i wykładnika izentropy.

z równania Mayera

z definicji izentropy

zatem

, a

4. Wyznaczenie temperatury powietrza po sprężaniu

Z równania izochory otrzymamy

, stąd:

5. Określenie bilansu energii wewnętrznej dla przemian odwracalnych

1 postać I zasady termodynamiki:

gdzie praca bezwzględna objętościowa

2 postać I zasady termodynamiki:

gdzie praca techniczna

6. Wyznaczenie przyrostu ilości ciepła doprowadzonego do układu w przemianie izochorycznej

Uwzględniając I zasadę termodynamiki dla przemiany izochorycznej, możemy napisać:

, bowiem V= const

a dV=0

Zasób energii wewnętrznej gazu doskonałego w układzie substancjalnym jest równy:

zaś jego elementarny przyrost określony jest wyrażeniem:

stąd bilans energii wewnętrznej przyjmie postać:

całkując powyższe równanie w granicach

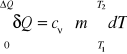
otrzymamy

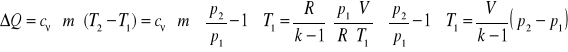
7. Wyznaczenie przyrostu zasobu entalpii gazu w układzie w przemianie izochorycznej

2 postać I zasady termodynamiki określona jest związkiem:

całkując powyższe równanie w granicach

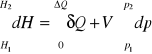
otrzymamy

8. Wyznaczenie przyrostu zasobu entropii gazu w układzie w przemianie izochorycznej.

Uwzględniając definicję entropii możemy zapisać:

całkując powyższe równanie w granicach

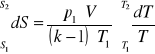
otrzymamy

9. Rachunek mian dla przyrostu ilości ciepła
   

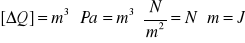
10. Rachunek mian dla przyrostu zasobu entalpii
    

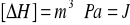
11. Rachunek mian dla przyrostu zasobu entropii
    

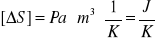
12. Obliczenie wartości przyrostu ilości ciepła ΔQ

13. Obliczenie wartości przyrostu zasobu entalpii ΔH

14. Obliczenie wartości przyrostu zasobu entropii ΔS

1

p₁

p₂

2

1

p

V

L_t

---