Zestaw 4a, Matematyka. Powtórzenia, Matematyka. Powtórzenia. Zestawy

Pobierz cały dokument zestaw.4a.matematyka.powtorzenia.matematyka.doc Rozmiar 590 KB

Fragment dokumentu:

Zestaw 4.cd

Granica ciągu liczbowego (bez zadań na dowodzenie). Interpretacja pojęcia granicy. Własności funkcji (parzystość, nieparzystość; różnowartościowość). Należy położyć nacisk na odczytywanie własności funkcji z wykresu.

10. Pokazać, że funkcja f(x) = x log(|x|) jest funkcją nieparzystą.

Rozwiązanie.

Dziedzina funkcji f jest zbiorem D_f = {x∈R: x ≠ 0}. Ponieważ dla x∈R |x| = |-x| zatem dla x∈D_f f(-x) = -x log(|-x|) = -x log(|x|) = -f(-x) a to oznacza na mocy definicji funkcji nieparzystej, że f jest funkcją nieparzystą .

11 Pokazać, że funkcja f zadana równością

na D_f = {x∈R: x ≠-2}, jest funkcją różnowartościową.

Rozwiązanie

Rozważmy x₁, x₂ ∈D i x₁ ≠ x₂ . Wtedy x₁ + 2 ≠ x₂ +2 a zatem również odwrotności są różne

1/(x₁ + 2) ≠ 1/(x₂ +2) i w konsekwencji 1/(x₁ + 2) + 1 ≠ 1/(x₂ +2) + 1 czyli f(x₁) ≠ f(x₂)

co wobec definicji różnowartościowości oznacza różnowartościowość f .

Zauważmy, że f ma postać kanoniczną funkcji homograficznej zatem przytoczone uzasadnienie może być powielone dla dowolnej homografii, skąd wyciągamy wniosek, że dowolna homografia jest funkcją różnowartościową.

Ćwiczenia.

Zadanie 4.1. Wypisz kilka wyrazów początkowych ciągu

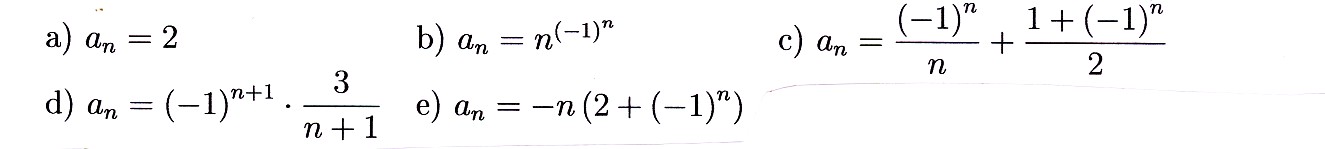
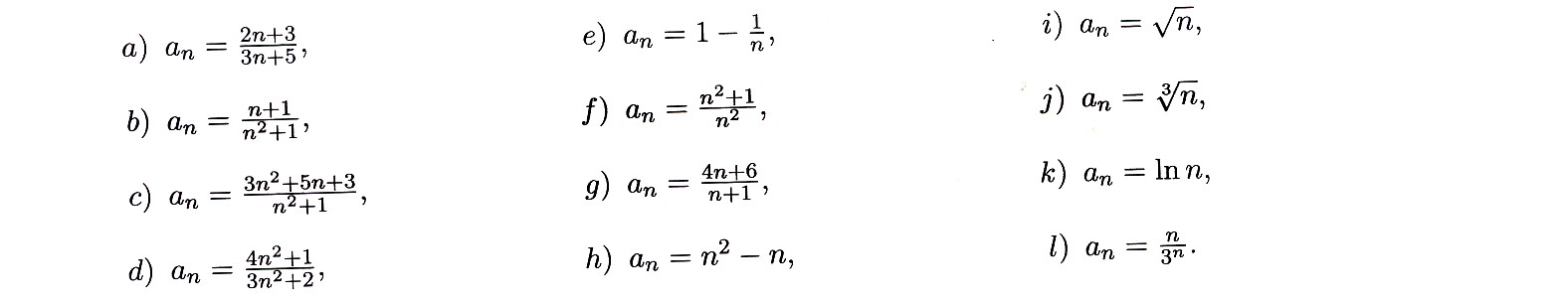
Zadanie 4.2 Zbadaj monotoniczność ciągu

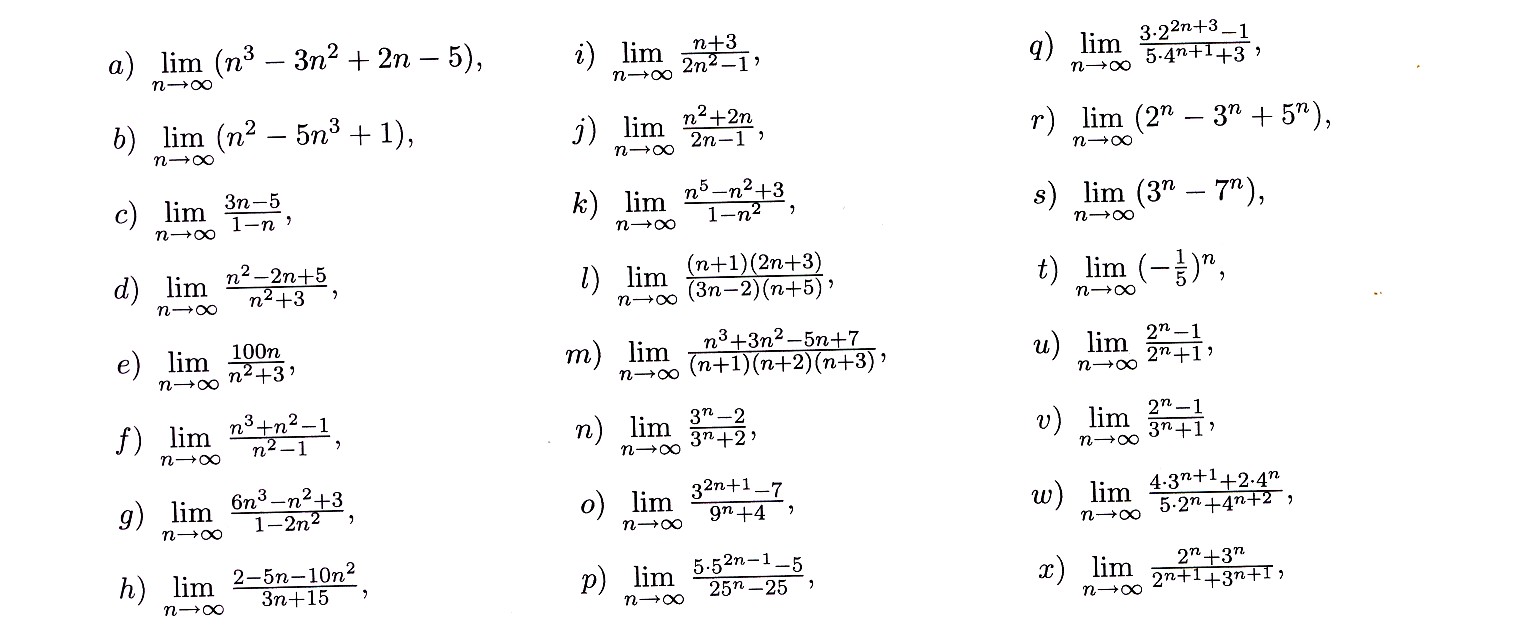
Zadanie 4.3. Oblicz granicę ciągu

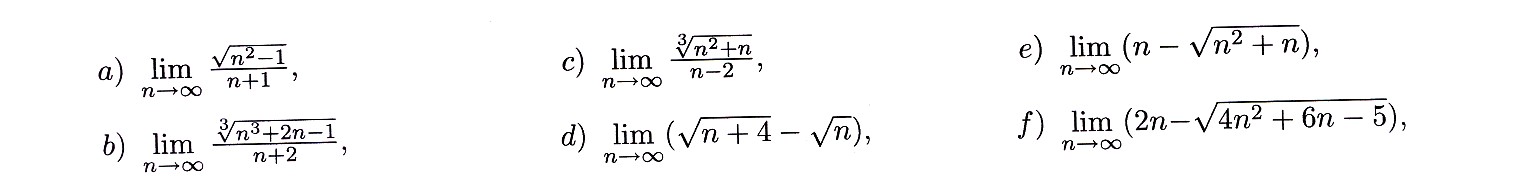
Zadanie 4.4 Wyznacz granicę ciągu

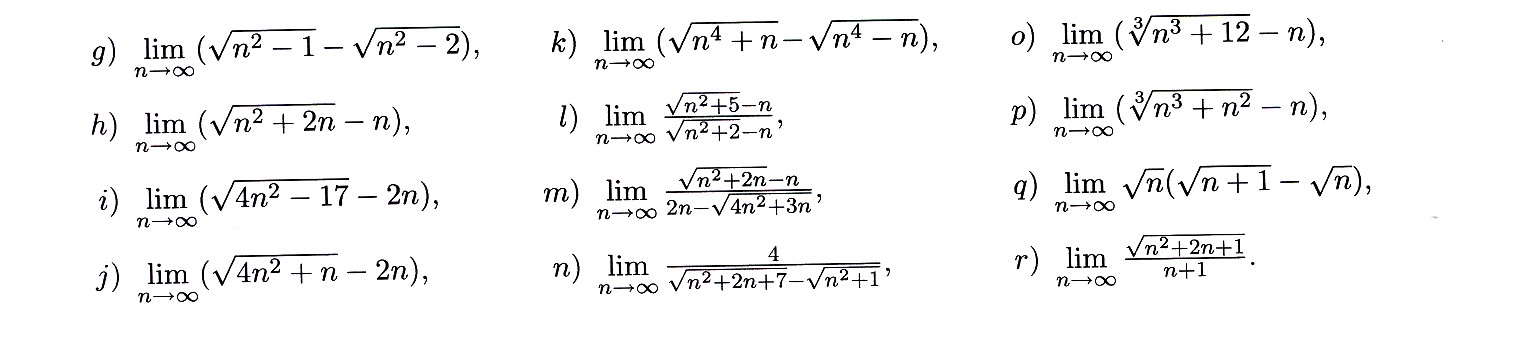
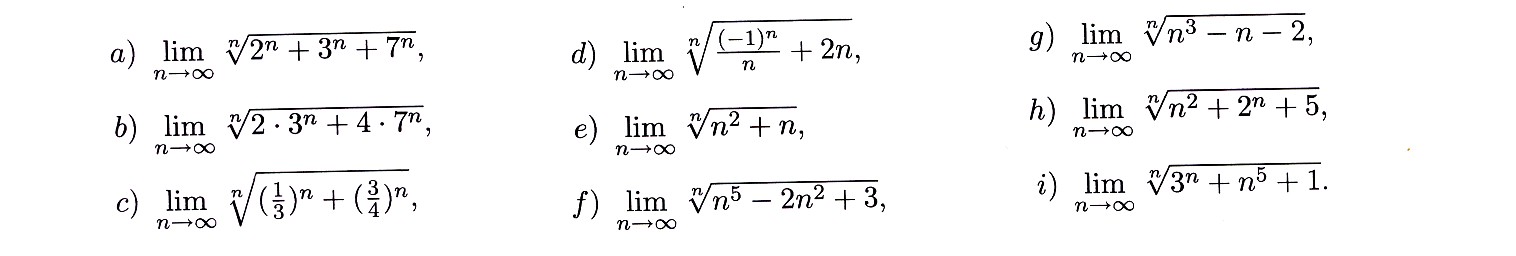
Zadanie 4.5 Stosując twierdzenie o trzech ciągach oblicz granicę ciągu

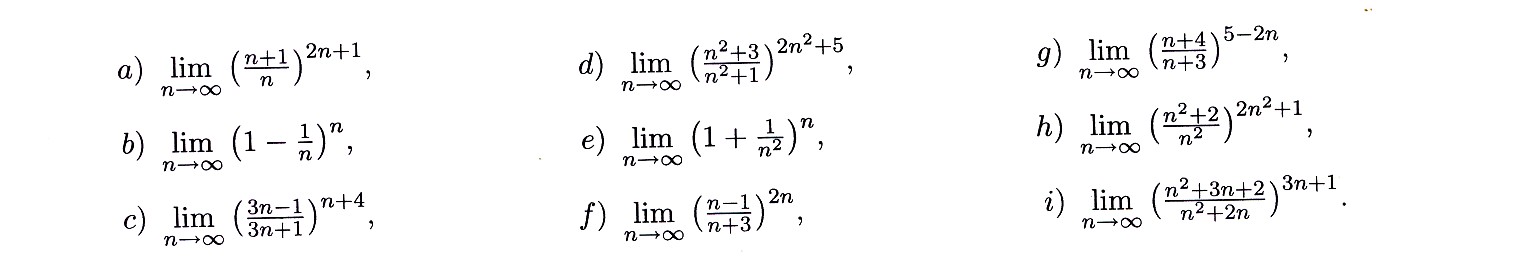
Zadanie 4.6 Obliczyć granicę ciągu wykorzystując definicję liczby Eulera e .

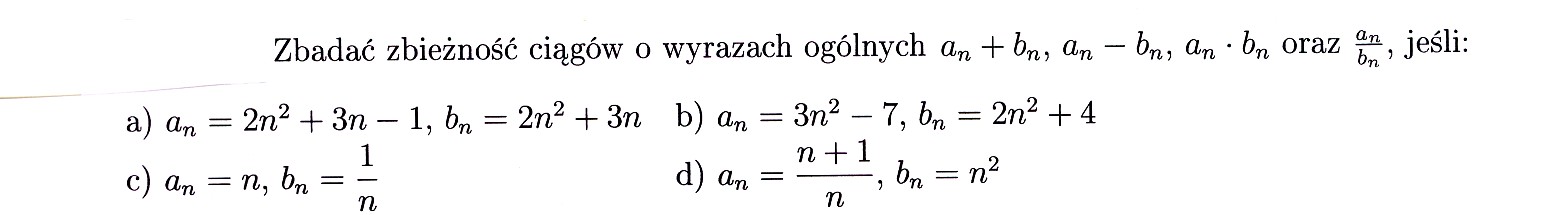
Zadanie 4.7

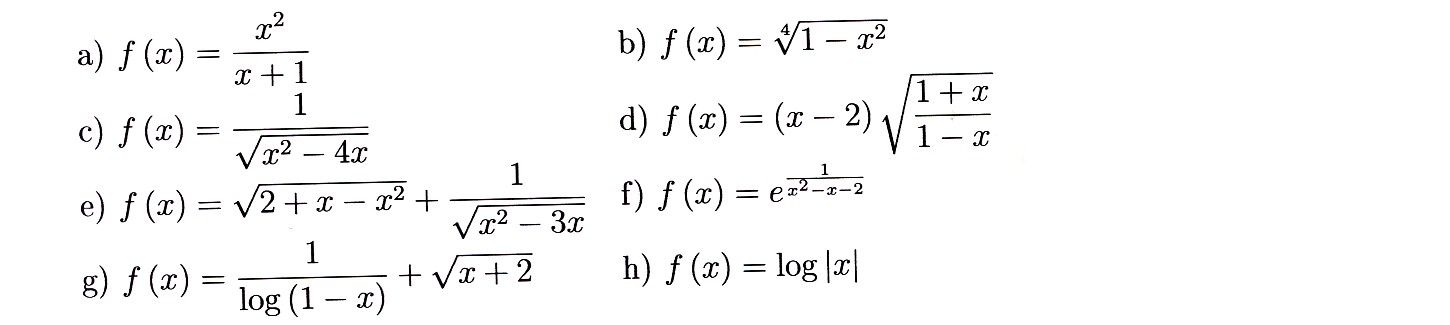
Zadamie 4.8 Wyznaczyć dziedziny funkcji

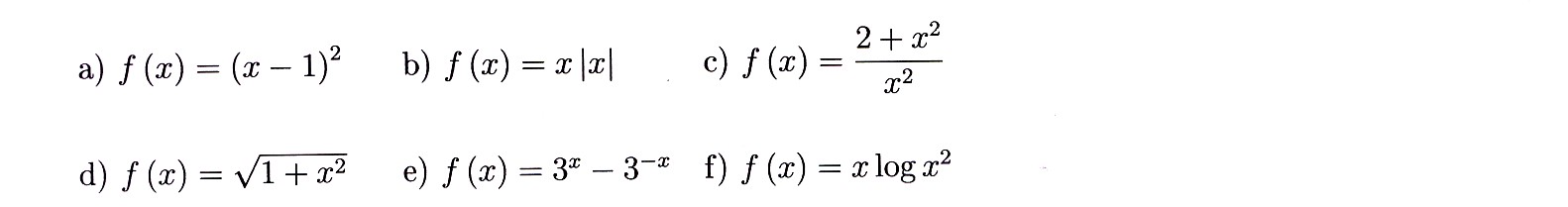
Zadanie 4.9 Zbadać, czy podane funkcje są parzyste czy nieparzyste.

g) f(x) = 2x³ - x h) f(x) = x²+3x-2 i) f(x) = x⁷-2x+1

Zadanie 4,10 Zbadać różnowartościowość podanych funkcji

a) f(x) = x - 11 b) f(x) = 2^x - 1 c) f(x) = x³ - x d) f(x) = 4x² - 13

e) f(x) = x⁴ + x² + 2 f) f(x) = |x - 1| g) f(x) = |x³| h) f(X) = x|x|

Zadanie 4.11 Znaleźć f(f(x)), g(g(x)), f(g(x)) i g(f(x)) dla f i g zadanych następująco

a) f(x) = x² , cg(x) = 2^x b) f(x) = log₂(x) , g(x) = x³

c) f(x) = log(x) , g(x) = 10^{x cc} d) f(x) = x^1/4 , g(x) = x⁴

Odpowiedzi.

Zadanie 4.1.

a) 2, 2, 2, 2

b) 1, 2, 1/3, 4

c) -1, 3/2, -1/3, 5/4

d) 3/2, -1, ľ, -3/5

e) -1, -6, -3, -12

Zadanie 4.2.

a) rosnący

b) malejący

Pobierz cały dokument zestaw.4a.matematyka.powtorzenia.matematyka.doc rozmiar 590 KB