Wydział Inżynierii Mechanicznej i Robotyki

TEORIA MASZYN I MECHANIZMÓW PRECYZYJNYCH

ANALIZA MECHANIZMU 1A

Marcin Matras, grupa 25, Mechatronika

Temat zadania:

Utworzono mechanizm czworoboku przegubowego zgodnie z zadanym schematem

dane:

m₂=6kg

J_S2=0,5833kg*m²

P₂=150N

M₃=150Nm

=

1. ANALIZA STRUKTURALNA MECHANIZMU

Ruchliwość mechanizmu jest równa 1.

Mechanizm jest klasy V.

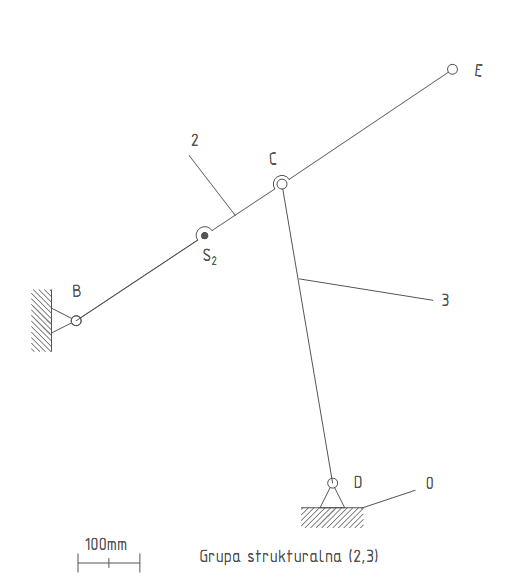
n=2

p₅=3

w_gr=0

grupa strukturalna klasy 2

Analizowany łańcuch kinematyczny jest mechanizmem kl. 2

2.ANALIZA KINEMATYCZNA MECHANIZMU METODĄ GRAFOANALITYCZNĄ

Obliczenia:

k_v =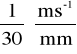
-podziałka prędkości

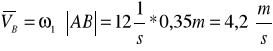
- kierunek wektora prostopadły do |AB|

Obliczam prędkość punktu C:

(1) V_C- ┴ |CD|; V_B- ┴ |AB|; V_CB- ┴ |BC|

(2) V_EB- ┴ |BE|

PLAN PRĘDKOŚCI:

Obliczono prędkości:

V_E= k*( V_E)=2,757 [m/s]

V_C= k*( V_C)=2,033 [m/s]

V_S2= k*( V_S2)=3,024 [m/s]

V_CB= k*( V_CB)=2,97 [m/s]

V_EB= k*( V_EB)=5,77[m/s]

V_S2B= k*( V_S2B)=2,09 [m/s]

Obliczono prędkośc kątowe poszczególnych członówi:

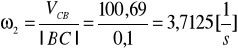
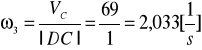
WYZNACZANIE PRZYSPIESZEŃ:

Obliczono a_B, a_C, a_CB:

Równanie przyspieszeń punktu C:

,
║ CD;
┴ CD ;
║ AB;
║ BC ;
┴BC

Z planu odczytano:

Równanie przyspieszenia punktu E:

(3)
║ EB;
┴ EB

Z planu odczytano:

Równanie przyspieszenia punktu S₂:

(3)
║ BC;
┴ BC

Z planu odczytano:

Obliczono przyspieszenia kątowe:

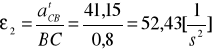
3.ANALIZA KINEMATYCZNA METODĄ ANALITYCZNĄ

3.ANALIZA KINEMATYCZNA PRZY POMOCY PROGRAMU SAM

3.1 Utworzono mechanizm w programie SAM

3.2 Utworzono wykres prędkości oraz przyspieszeń poszczególnych punktów

Porównanie wyników analizy kinematycznej

		Metoda grafoanalityczna	Metoda analityczna	Wyniki z prgramu SAM
1	VB	4,2	4,2	4,2000
2	VC	2,0934	2,0315	2,1310
3	VE	2,5975	2,6580	2,6975
4	VS2	2,0921	2,114	2,121
5	ω2	3,7125	3,72	-
6	ω3	2,0331	2,121	-
7	aB	50,4	50,4	50,400
8	aC	4,133	4,181	4,2141
9	aE	85,33	85,92	86,512
10	aS2	52,231	52,612	53,097
11	ε2	51,334	51,312	-1935,01
12	ε3	60,231	60,248	-

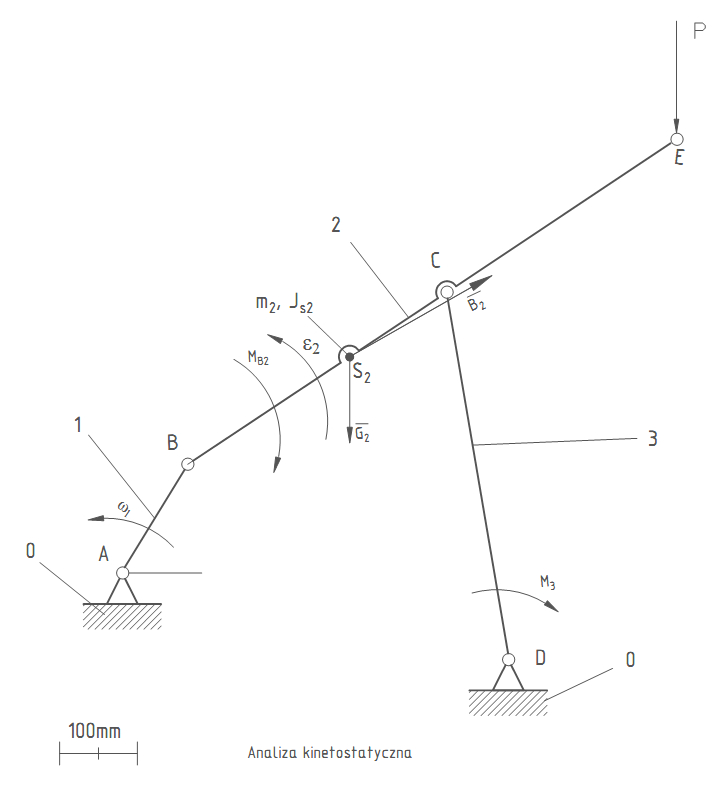
6. ANALIZA KINETOSTATYCZNA

Dane:

P₂ = 150 N

M₃=150Nm

I_S2=0,58333kg*m²

6.2 Obliczono siłę cięzkości G₂, siłę bezwładności
oraz moment od sił bezwładności
:

G₂=6kg*9,81m/s²=58,26N

= -m₂

= m₂
= 6kg*52,3 m/s²

= 313,98 [N]

= -I_S2

= I_S2ε₂ = 0,58333*60,23m/s²

== 35 [Nm]

6.3 Obliczono siły działające na człony 2 i 3

6.3.1 Reakcje
i
podzielono na składowe styczne (
,
) i normalne(
,
)

6.3.2 Obliczono wartość siły
oraz
:

=
* BC + G₂h₂ + B₂h₁- Ph₃-M_B2 = 0

=

=

= 56,68 [N]

=
* CD - M₃ = 0

=

=
= 150 [N]

Równanie posiada teraz dwie niewiadome, którymi są wartości sił
i

6.4.4 Równanie równowagi sił:

+
+
+
+
+
+
= 0

Przyjęto podziałkę k_R = 3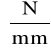

Wykreślne rozwiązanie równania równowagi sił.

6.4.5 Obliczono wartość wyznaczonych sił
i
:

Rⁿ₁₂ =k*(R₁₂) =3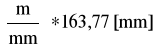

R₁₂=491,31 [N]

R₁₂ =k*(R₁₂) =3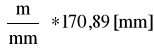

R₁₂=512,67 [N]

Rⁿ₀₃ =k*(R₁₂) =3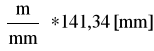

R ⁿ₀₃=424,02 [N]

R₀₃₌k*(R₀₃) =30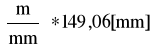

R₀₃ = 447,15 [N]

6.4.6 Obliczono wartość siły R₃₂

+
+
+
= 0

Wykreślne rozwiązanie równania równowagi sił

=k*(
)=3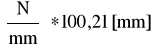

= 600,63 [N]

6.5 Dokonano analizy sił działających na człon napędzający

Równania równowagi sił:

+
= 0

= -

= 491,31 [N]

6.5.1 Obliczeno wartość momentu równoważącego M_R1

M_R1 - R_21*h₄ = 0

M_R1 = R_21*h₄

M_R1 = 491,31 * 11,78mm = 5,7876 [Nm]

7.ANALIZA KINETOSTATYCZNA METODĄ MOCY CHWILOWYCH

Obliczono moment równoważący:

M_R1ω₁ + P₂V_Ecos(α₁) + G₂V_S2cos(α₃)+ B₂V_S2cos(α₂) + M_B2 ω₂ + M₃ ω₃ = 0

M_R1 =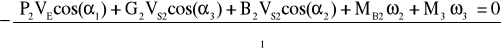

M_R1= -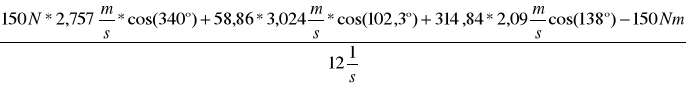

M_R1= -5,8421 [Nm]

7.ANALIZA KINETOSTATYCZNA PRZY POMOCY PROGRAMU SAN

7.1 Mechanizm utworzony w programie SAM

7.2 Utworzono wykresy zależności sił działających na poszczególne punkty od czasu

Porównanie wyników analizy kinematycznej

		Metoda grafoanalityczna	Metoda mocy chwilowych	Program SAM
1	P01	491,31	-	491,14
2	P12	491,31	-	491,14
3	P32	600,63	-	600,12
4	P03	149,06	-	149,12
5	B2	313,98	-	313,32
6	Mzr1	-5,7876	-5,7421	-

---