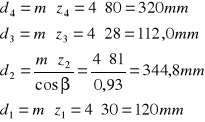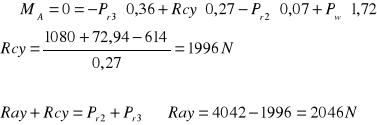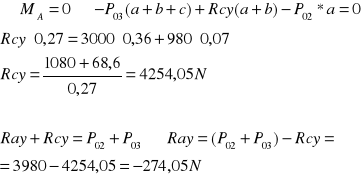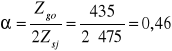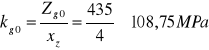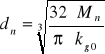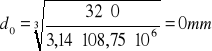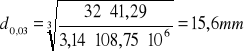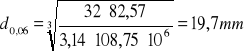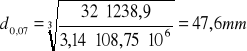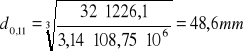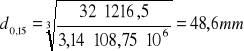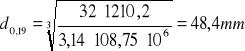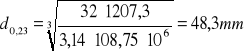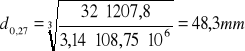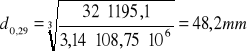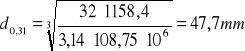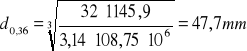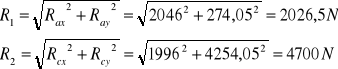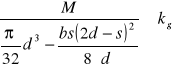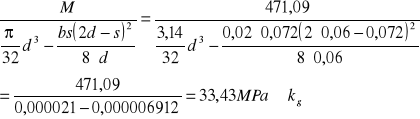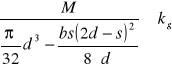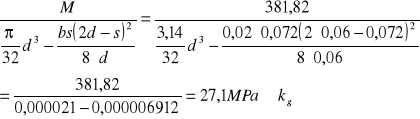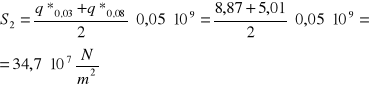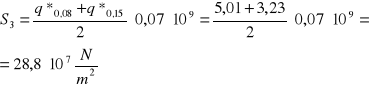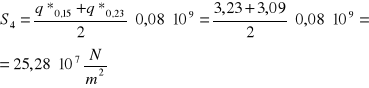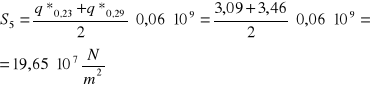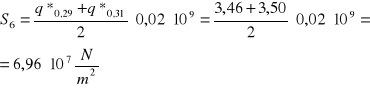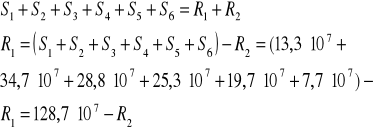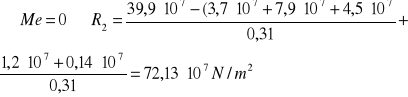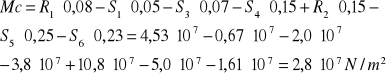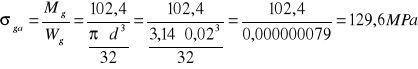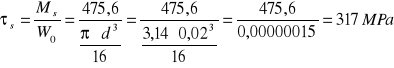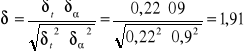Ms4 = 1000 kGcm z3 =28 z4 = 80 m = 4 mm z2 = 81 β = 20^o d4 = 344,8 mm Ms4 = 245 Nm α = 20^o d3 = 112 mm Ms = 475,6 Nm α = 45^o Ms = 1689,5 Nm d2 = 344,8 mm β = 20^o Pr2 = 1042N Pr3 = 3000N Pw = 356N a = 70 mm b = 200 mm c = 90 mm e = 172,5 mm a = 70 mm Ray = 2046 N Ray = 2046 N Pr2 = 1042N a = 70 mm b = 200 mm Ray = 2046 N Rcy = 1996 N Pr2 = 1042N a = 70 mm b = 200 mm a = 70 mm b = 200 mm c = 90 mm P02 = 980N P03 = 3000N a = 70 mm Ray = -274,05 N a = 70 mm b = 200 mm Ray =-274,05 N P02 = 980N a = 70 mm b = 200 mm c = 90 mm Ray =-274,05 N Rcy = 4254,05 N P02 = 980N Ray =-274,05 N Ray =-274,05 N P02 = 980N Ray =-274,05 N P02 = 980N Rcy = 4254,05 N a = 70 mm b = 200 mm Ray = 2046 N Pr2 = 1042N Ray = 2046 N Pr2 = 1042N Ray = 2046 N Pr2 = 1042N Rcy = 1996 N α = 0,43 Ms = 1689,5 Nm Mw0=0 Nm Mw0,03=41,29Nm Mw0,06=82,57Nm Mw0,07=471,09 Nm Mw0,11=436,17 Nm Mw0,15=408,34 Nm Mw0,19=389,2 Nm Mw0,23=380,15 Nm Mw0,27=381,82 Nm Mw0,29=339,41 Nm Mw0,32=169,71Nm Mw0,36=0Nm kg0=108,75MPa Mz0=0 Nm Mz0,03=41,29 Nm Mz0,06=82,57 Nm Mz0,07=1238,9 Nm Mz0,11=1226,1Nm Mz0,15=1216,5Nm Mz0,19=1210,2Nm Mz0,23=1207,3 Nm Mz0,27=1207,8Nm Mz0,29=1195,1Nm Mz0,32=1158,4Nm Mz0,36=1145,9Nm Rax = 2046 N Rcx = 1996 N Ray =-274,05 N Rcy = 4254,05N Pw= 356 N l = 6 -liczba lat z = 3- liczba zmian V = 1 R2= 4700 N X = 1 Y = 0 q =3 dla łożysk kulkowych Lh = 29200 h n=1500obr/min R1 =2026,5 N Pw= 356 N V = 1 C0 = 64000 N R1 = 2026,5N Pw= 356 N V = 1 X = 0,56 Y = 2,30 Ms =1689,5 Nm d·=60 mm s = 7,2 mm z = 1 ilość wpustów pdop = 253 MPa M0,08=471,09 Nm S = 7,2 mm d = 60 mm b = 20 mm kg0=108,75 MPa M031=381,82 Nm S = 72 mm d = 60 mm b = 20 mm kg0=108,75MPa Mz0=0 Nm Mz0,03=41,29 Nm Mz0,06=82,57 Nm Mz0,07=1238,9 Nm Mz0,11=1226,1Nm Mz0,15=1216,5Nm Mz0,19=1210,2Nm Mz0,23=1207,3 Nm Mz0,27=1207,8Nm Mz0,29=1195,1Nm Mz0,32=1158,4Nm Mz0,36=1145,9Nm d0,03 =15,6mm d0,07=47,6 mm d0,15=48,6 mm d0,23=48,3 mm d0,27=48,3 mm d0,29=48,2 mm d0,31=47,7 mm d0,36=47,7 mm q*0,03=8,87·10^-9 q*0,08=5,01·10^-9 q*0,15=3,23·10^-9 q*0,23=3,09·10^-9 q*0,29=3,46·10^-9 q*0,31=3,50·10^-9 S1=13,3·10^7N/m^2 S2=34,7·10^7N/m^2 S3=28,8·10^7N/m^2 S4=25,3·10^7N/m^2 S5=19,7·10^7N/m^2 S6=7,0·10^7N/m^2 S1=13,3·10^7N/m^2 S2=34,7·10^7N/m^2 S3=28,8·10^7N/m^2 S4=25,3·10^7N/m^2 S5=19,7·10^7N/m^2 S6=7,0·10^7N/m^2 R1=56,6·10^7 N/m^2 R2=72,1·10^7 N/m^2 m = 10 Mc=2,8·10 ^7N/m^2 E=2,1·10^5 MPa R1 = 56,6·10^7 N/m^2 R2= 72,1·10^7 N/m^2 Rm = 520 MPa Dla stali C35 Mg=102,4Nm Zg0=208 MPa ε=0,81 =1,62 αga=129,6 MPa Zg0=208 MPa Ms =475,6 Nm Zss=124,8MPa =1,62 ε=0,91 τs=317 =0,22 =0,9

Temat B 10/II Przeliczenie wartości Ms2 na kNm Obliczenie momentu skręcającego na przekładni pasowej Obliczenie średnic kół z4 z3 z2 i z1 Obliczenie momentu skręcającego na przekładni zębatej [ z1 z2 ] Ms3 = Ms - Moment skręcający na wale Obliczenie sił występujących na kole z3 Obliczenie sił działających na koło z2 P0 - siła obwodowa Pw - siła poosiowa Pr - siła promieniowa Obliczenie wartości momentów zginających wału W tym celu wał rozpatrujemy jako belkę podpartą w łożyskach i obciążonej siłami. Każdą siłę rozpatrujemy w płaszczyźnie jej działania. Rozpatrujemy płaszczyznę poziomą xz Obliczanie momentów gnących 0 ≤ z ≤ a M(z) = Ray z M(0) = 2046 · 0 kNm M(0,07) = 2046 · 0,07= 143,72 Nm a ≤ z ≤ a +b M(z) = Ray z- Pr2 (z-a) - Pw · e M(0,08) = 2046 · 0,07 - 0 - 614 = -470,8 Nm M(0,23) = 2046 · 0,27 - (1042·0,2) - 614 = -270 Nm a +b≤ z ≤ a + b + c M(z) = Ray z- Pr2 (z-a) + Rcx (z-[a+b]) - Pw · e M(0,23) = 2046 · 0,27 - (1042·0,2) + 1996 · 0 - 614 = = -270 Nm M(0,31) = 2046 · 0,36 - (1042·0,29) + 1996 · 0,09 - 614 = 0 Nm Rozpatrujemy płaszczyznę yz Obliczanie momentów gnących 0≤ z ≤ a M(z) = Ray z M(0) = -274,05 · 0 = Nm M(0,08) = = -274,05 · 0,08 = - 36,2Nm a ≤ z ≤ a + b M(z) = Ray z - P02 (z-a) M(0,08) = -274,05 · 0,07 - 980 · 0= -32 Nm M(0,23) = -274,05 · 0,27 - 980 · 0,2= -319,5 Nm a + b≤ z ≤ a + b + c M(z) = Ray z- P02 (z-a)-Rcy (z-[a+b]) M(a+b) = (-274,05 · 0,27) -980*(0,27- 0,07)+4254,05 · 0 = -270 Nm M(a+b+c) = -(-274,05 · 0,36) -980*(0,36- 0,07) + 4254,05 · (0,36-0,27) = 0 Nm Wyznaczenie momentów gnących w kolejnych punktach wału: Płaszczyzna yoz: M(z) = Ray·z M(0) = -274,05 · 0 = 0 Nm M(0,03) = -274,05 · 0,03 = -5,48 Nm M(0,06) = -274,05 · 0,06 = -10,96 Nm M(0,07) = -274,05 · 0,07 = -19,18 Nm a ≤ z ≤ a + b M(z) = Ray·z - P02 · (z-a) M(0,07) = -274,05 · 0,07 - 980 ·0 = -19,18 Nm M(0,11) = -274,05 · 0,11 - 980 ·0,07 = -69,34 Nm M(0,15) = -274,05 · 0,15 - 980 ·0,08 = -119,5 Nm M(0,19) = -274,05 · 0,19 - 980 ·0,12= -169,6 Nm M(0,23) = -274,05 · 0,23 - 980 ·0,16 = -219,83 Nm M(0,27) = -274,05 · 0,27 - 980 ·0,2 = -270 Nm a + b≤ z ≤ a + b + c M(z) = Ray · z - P02(z-a) + Rcy[z-(a+b)] M(0,27) = -274,05 · 0,27 - 980 ·0,2 + 4254,05 · 0 = - 274,05 Nm M(0,32) = -274,05 · 0,32 - 980 ·0,25 + 4254,05 · 0,05 = - 210,09 Nm M(0,36) = -274,05 · 0,36 - 980 ·0,29 + 4254,05 · 0,09 = 0 Nm Płaszczyzna xoz: M(z) = Ray · z M(0) = 2046 · 0= 0 Nm M(0,03) = 2046 · 0,03 = 40,92 Nm M(0,06) = 2046· 0,06 = 81,84 Nm M(0,08) = 2046 · 0,08 = 143,22 Nm M(z) = Ray · -Pr2 (z-a) - Pw · e M(0,07) = 2046 · 0,08 - 0 - 128 = - 470 Nm M(0,11) = 2046 · 0,12 - 1042 ·0,04- 614 = - 430,62 Nm M(0,15) = 2046 · 0,15 - 1042 ·0,07- 614 = - 390,46 Nm M(0,19) = 2046 · 0,18 - 1042 ·0,10- 614 = - 350,3 Nm M(0,23) =2046· 0,21 - 1042 ·0,13- 614 = - 310,14 Nm M(0,27) = 2046 · 0,23 - 1042 ·0,15- 614 = - 269,98 Nm M(z) = Ray · -Pr2 (z-a) +Rcy [z-(a+b)] - Pw · e M(0,27) = 2046 · 0,26 - 1042 · 0,18 + 1996 · 0,03-614 = -240 Nm M(0,32) = 2046 · 0,29 - 1042 · 0,21 + 1996 · 0,06-614 = -120 Nm M(0,36) = 2046 · 0,31 - 1042 · 0,23 + 1996 · 0,08-614 = 0 Nm Wyznaczenie wypadkowych momentów zginających w kolejnych punktach wału: Obliczenie współczynnika redukującego naprężenia styczne do normalnych Dla stali 40HN: Zgo = 435 MPa Zsj = 475 MPa Wyznaczenie momentów zredukowanych w oparciu o hipotezę Hubera Teoretyczne średnice wału w charakterystycznych przedziałach Przyjmuje współczynnik zapasu wytrzymałości xz = 4, a więc: Kształtowanie wału wg wymagań technologicznych i montażowych Średnicę wału w łożyskach przyjmuje jako większą od średnic obliczeniowych dł1 = 40 mm dł2 = 75 mm Średnicę wału dla otworu piasty [dla obu kół zębatych] przyjmuje 48, aby była większa od średnicy obliczeniowej i możliwe było osadzenie koła bez uszkodzenia powierzchni pod łożysko dC =60 mm Z jednej strony piasty zakładam średnicę kołnierza dk =90 mm Dobór łożysk tocznych Reakcja wypadkowa działająca na łożysko: Wstępnie zakładam, że siłę Pw przejmie łożysko obciążone mniejszą siłą poprzeczną. Obliczenie liczby godzin pracy łożysk Określenie współczynników ft i fd Założenie: wał pracuje w temperaturze do 150^oC - ft = 1 Założenie: wał pracuje spokojnie, bez uderzeń - fd = 1 Łożysko nr 2: V - współczynnik przypadku obciążenia, dla ruchomego wału V = 1 Obciążenie zastępcze dla łożyska 2: Obliczenie współczynnika trwałości: Wymagana nośność łożyska: Z katalogu dobieram łożysko walcowe 215, dla którego C = 145000 N Łożysko nr 1: (zakładam łożysko 6408) Ponieważ > e należy dobrać współczynniki X i Y Wartość współczynnika X = 0,56 Z katalogu dobieram wartość współczynnika Y = 2,30 Obliczenie obciążenia zastępczego: Wymagana nośność dynamiczna łożyska 1: Nośność dynamiczna przyjętego łożyska 6408 wynosi 64000 N > 32782,7 N Obliczenie połączeń piast· kół zębatych z czopem wału Z katalogu dobieram wpust o wymiarach b x h 8 x 11 oraz głębokości s = 3,7. Dla połączenia spoczynkowego i wpustu wykonanego ze stali 40HN przyjęto pdop = 253 MPa Rzeczywista długość wpustu: Przyjmuje długość znormalizowaną l = 50mm Sprawdzenie wytrzymałości na zginanie po uwzględnieniu w czopach otworów pod wpusty: Koło zębate z2: Koło zębate z3: Obliczenie ugięcia wału i strzałek obrotu. Maksymalną strzałkę ugięcia określam na podstawie wypadkowego momentu gnącego. Wykres obciążenia fikcyjnego q*[dla punktów charakterystycznych]: Wyznaczenie wektorów S umieszczonych w środkach ciężkości pól (rys. powyżej): Wyznaczenie reakcji fikcyjnych: Wyznaczenie strzałki ugięcia Maksymalny moment fikcyjny znajduje się w punkcie C belki i wynosi: Obliczenie kątów ugięcia w łożyskach: Obliczenia zmęczeniowe wału: Zakładam rzeczywisty współczynnik bezpieczeństwa - dokładne wykonanie, jednorodny materiał, dokładne oblicznia Z analizy teoretycznych przekrojów wału i przyjętego zarysu rzeczywistego wynika, ze najbardziej narażonym przekrojem jest przekrój pod łożysko nr 1. Rzeczywisty współczynnik bezpieczeństwa wg naprężeń normalnych: Z tablic odczytuje współczynnik wielkości przedmiotu: Współczynnik uwzględniający działanie karbu i stan powierzchni: Wartości oraz odczytano z tablic: = 1,6 - współczynnik działania karbu = 1,02 - współczynnik stanu powierzchni ( obróbka szlifowaniem ) Rzeczywisty współczynnik bezpieczeństwa wg naprężeń normalnych: Rzeczywisty współczynnik bezpieczeństwa wg naprężeń stycznych: Z tablic odczytuje współczynnik wielkości przedmiotu: Współczynnik uwzględniający działanie karbu i stan powierzchni: Wartości oraz odczytano z tablic: · = 1,6 - współczynnik działania karbu = 1,02 - współczynnik stanu powierzchni ( obróbka szlifowaniem ) Współczynnik wrażliwości cyklu: (stal o niskiej zawartości węgla) Rzeczywisty współczynnik bezpieczeństwa wg naprężeń stycznych Rzeczywisty współczynnik bezpieczeństwa dla obciążeń złożonych: Literatura: Mazanek - „Postawy Konstrukcji Maszyn” Wolny, Siemieniec - „Wytrzymałość Materiałów” Wykłady z Podstaw Konstrukcji Maszyn

Ms4 = 98 Nm d3 = 112 mm d4 = 320 mm d2 = 344,8 mm Ms3 = 1689,5 Nm P03 = 3000 N Pr3 = 3000 N P3 = 3894 N P02 = 980 N Pr2 = 1042 N Pw= 356 N Rax = -356 N Ray = 2046 N Rcy = 1996 N Ray = -274,05 N Rcy = 4254,05 N Mw0=0 Nm Mw0,03=41,29Nm Mw0,06=82,57Nm Mw0,07=471,09 Nm Mw0,11=436,17 Nm Mw0,15=408,34 Nm Mw0,19=389,2 Nm Mw0,23=380,15 Nm Mw0,27=381,82 Nm Mw0,29=339,41 Nm Mw0,32=169,71Nm Mw0,36=0Nm α = 0,46 Mz0=0 Nm Mz0,03=41,29 Nm Mz0,06=82,57 Nm Mz0,07=1238,9 Nm Mz0,11=1226,1Nm Mz0,15=1216,5Nm Mz0,19=1210,2Nm Mz0,23=1207,3 Nm Mz0,27=1207,8Nm Mz0,29=1195,1Nm Mz0,32=1158,4Nm Mz0,36=1145,9Nm kg0=108,75MPa d=0 Nm d0,03 =15,6mm d0,06 =19,7 mm d0,07=47,6 mm d0,11=48,6 mm d0,15=48,6 mm d0,18=48,4 mm d0,21=48,3 mm d0,23=48,3 mm d0,27=48,3 mm d0,29=48,2 mm d0,31=47,7 mm d0,36=47,7 mm R1 = 2026,5 N R2= 4700 N Lh = 52560 h C = 78897,6 N e = 1,19 P1 = 1953,64 N l = 50mm q*0,03= 0,0014·10^-9 q*0,08=0,005·10^-9 q*0,15=4,47·10^-9 q*0,23=4,52·10^-9 q*0,27=0,004·10^-9 q*0,29=4,51·10^-9 q*0,31=4,56·10^-9 q*0,31=4,62·10^-9 S1=13,3·10^7N/m^2 S2=34,7·10^7N/m^2 S3=28,8·10^7N/m^2 S4=25,3·10^7N/m^2 S5=19,7·10^7N/m^2 S6=7,0·10^7N/m^2 R1 = 56,6·10^7 N/m^2 R2= 72,1·10^7 N/m^2 Mc=2,8·10^7N/m^2 fc=0,13 mm V1=0,0027 rad V2=0,0034 rad Zg0=208 MPa ε=0,91 αga=129,6 MPa =1,62 =0,9 Zs0=124,8 MPa ε=0,81 τs=317MPa =0,22 =1,91

- 15 -

---