TEORIA MASZYN I MECHANIZMÓW

Tomasz Dutka

GR 8A

ROK IIA

TEMAT: ANALIZA KINEMATYCZNA I KINETOSTATYCZNA MECHANIZMU DŹWIGNIOWEGO.

Zgodnie z numerem i wariantem liczbowym zadania przyjąłem wymiary mechanizmu i położenie jak na rysunku.

AB = 300 mm ω₁ = 20 s^-1

BC = 600 mm φ₁ = 45°

CD = 600 mm

BF = 300 mm

FE =300 mm

DS3 = 300 mm

1. ANALIZA STRUKTURALNA MECHANIZMU.

• RUCHLIWOŚĆ I KLASA MECHANIZMU.

AB - człon napędzający

BC i CD - człony ruchome

Ruchliwość mechanizmu:

n = 3 - liczba członów

p₄ = 0 - liczba par kinematycznych czwartej klasy

p₅ = 4 - liczba par kinematycznych piątej klasy

w = 3n - 2p₅ - p₄

w = 3*3 - 2*4 - 0

w = 1

Podział mechanizmu na grupy strukturalne:

Analizowany mechanizm jest mechanizmem klasy II

2. ANALIZA KINEMATYCZNA MECHANIZMU

1. MODEL MECHANIZMU W PORGRAMIE AKM

Na podstawie przeprowadzonej analizy strukturalnej ustaliłem, że model mechanizmu musi zawierać człon napędzający oraz grupę oznaczoną w programie AKM symbolem 0-0-0

Człon napędzający:

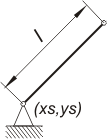
Parametry:

- xs = 0; ys = 0.1

- l = 0.3 [m]

- omega = 20 1/s

- kierunek obrotu - w lewo

Grupa strukturalna 2, 3 ( 0-0-0 )

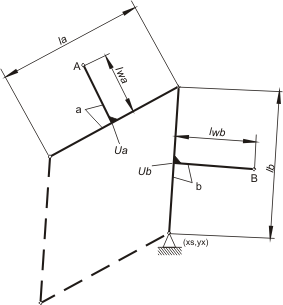
Parametry:

- xs = 0.7; ys = 0

- la = 0.6 [m]

- lb = 0.6 [m]

- lwa = 0.3 [m]

- lwb = 0.001 [m]

- Ua = 0

- Ub = 0

Po ustaleniu wymiarów przeprowadziłem symulację ruchu mechanizmu oraz analizę kinematyczną.

1. METODA GRAFOANALITYCZNA (METODA PLANÓW)

k₁ = 0,001
- podziałka rysunkowa mechanizmu.

AB = 0,3 m

BC = 0,6 m

CD = 0,6 m

BF = 0,3 m

FE = 0,3 m

DS3 = 0,3 m

ω₁ = 20 s^-1

Analiza prędkości.

Prędkość punktu B V_B = ω₁ * AB = 6

Podziałkę prędkości przyjmuję k_v = 0,05

Długość wektora prędkości punktu B na rysunku wynosi (V_B) =
=
=120 [mm]

Równanie prędkości punktu C:
=
+

Równanie prędkości punktu E:
=
+

=
+

Plan prędkości:

Rys. 5

V_C = 2,012

V_E = 3,4735

V_CB = 4,679

V_EB = 3,3345

V_EC = 3,3085

V_S3 = 1,006

Na podstawie planu obliczyłem:

ω₂ =
= 7,798 [s^-1]

ω₃ =
= 3,353 [s^-1]

Analiza przyspieszeń

Przyspieszenie punktu B: a_B =
=
AB = 120

Podziałkę przyspieszeń przyjmuję k_a = 2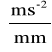

Długość wektora przyspieszeń punktu B na rysunku wynosi:
=
= 60 [mm]

Równanie przyspieszeń punktu C:
+
=
+
+

Równania przyspieszeń punktu E:
=
+
+

=
+
+

=
=
CD = 6,747 (
) = 3,37 [mm]

=
=
BC = 36,48 (
) = 18,24 [mm]

=
=
EB = 26,22 (
) = 13,1 [mm]

=
=
EC = 25,81 (
) = 12,9 [mm]

plan przyspieszeń:

Z planu przyspieszeń wynika: = 175,14 = 195,26 = 121,8 = 86,52 = 85,28 = 87,57

Na podstawie planu przyspieszeń obliczyłem: ε2 = = = 203 [s^-2] ε3 = = = 293,43 [s^-2] Na podstawie planu przyspieszeń zaznaczyłem zwroty przyspieszeń kątowych członów 2 i 3 na rys. 8.

1. ANALIZA KINEMATYCZNA MECHANIZMU - METODA ANALITYCZNA





+
+
+
+
= 0

l₁cosφ₁ + l₂cosφ₂ + l₃cosφ₃ + l₄cosφ₄ + l₅cosφ₅ = 0 (1)

l₁sinφ₁ + l₂sinφ₂ + l₃sinφ₃ + l₄sinφ₄ + l₅sinφ₅ = 0 (2)

Po podstawieniu wartości liczbowych wzory są następujące:

0,3cos45° + 0,6cosφ₂ + 0,6cosφ₃ - 0,7 = 0

0,3sin45° + 0,6sinφ₂ + 0,6sinφ₃ + 0,1 = 0

0,6cosφ₂ + 0,6cosφ₃ - 0,4879 = 0 |:0,6

0,6sinφ₂ + 0,6sinφ₃ + 0,3121 = 0 |:0,6

cosφ₂ + cosφ₃ - 0,8132 = 0

sinφ₂ + sinφ₃ + 0,5202 = 0

cosφ₂ - 0,8132 = -cosφ₃ |()² (3)

sinφ₂ + 0,5202 = -sinφ₃ |()²

cos²φ₂ - 1,6264cosφ₂ + 0,6613 = cos²φ₃

sin²φ₂ + 1,0404sinφ₂ + 0,2706 = sin²φ₃

+

1 - 1,6264cosφ₂ + 1,0404sinφ₂ + 0,9319 = 1

-1,6264cosφ₂ + 0,0404sinφ₂ + 0,9319 = 0 |: (-1,6264)

cosφ₂ - 0,6397sinφ₂ - 0,5729 = 0

Oznaczam A = -0,5729 oraz B = -0,6397

cosφ₂ + Bsinφ₂ + A = 0

cosφ₂ +A = Bsinφ₂ |()²

cos²φ₂ + 2Acosφ₂ + A² = B²sin²φ₂

sin²φ₂ = 1 - cos²φ₂

cos²φ₂ + 2Acosφ₂ +A² - B²(1 - cos²φ₂) = 0

cos²φ₂ +2Acosφ₂ + A² - B² +B²cos²φ₂ = 0

(1 + B²)cos²φ₂ + 2Acosφ₂ + (A² - B²) = 0

Po podstawieniu w = cosφ₂ otrzymuję:

[1 +(-0,6397)²]w² + 2*(-0,5729)w + [(-0,5729)² - (-0,6397)²] = 0

1,4092w² - 1,1458w - 0,081 = 0

∆ = 1,7694


= 1,3302

w₁ =
= -0,0654

w₂ =
= 0,8785

cosφ₂₍₁₎ = w1

cosφ₂₍₂₎ = w2

φ₂₍₁₎ = arccosw1

φ₂₍₂₎ = arccosw2

φ₂₍₁₎ = arccos(-0,0654) = 93,44°

φ₂₍₁₎ = 360° - 93,44° = 266,56°

φ₂₍₂₎ = arccos(0,8785) = 28,32°

_{Kąt φ2(1) = 266,56° dotyczy symetrycznego położenia mechanizmu (linią przerywaną) względem osi przechodzącej przez punkty B i D.}

Kąt φ₃ wyliczam na podstawie równania (3):

cosφ₃₍₁₎ = 0,8132 + 0,0654 = 0,8786

cosφ₃₍₂₎ = 0,8786 = -0,0654

φ₃₍₁₎ = 28,32°

φ₃₍₂₎ = 266,56°

Po zróżniczkowaniu równania (1) otrzymuję

-ω₁l₁sinφ₁ - ω₂l₂sinφ₂ - ω₃l₃sinφ₃ = 0 (4)

gdzie ω₁ =
; ω₂ =
; ω₃ =


ω₁l₁sin(φ₁ - φ₂) + ω₂l₂sin(φ₂ - φ₂) + ω₃l₃sin(φ₃ - φ₂) = 0

ponieważ ω₂l₂sin(φ₂ - φ₂) = 0 to mogę obliczyć

ω₃ = -


po podstawieniu danych liczbowych jest

ω₃ = -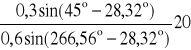
= 3,35 [s^-1]

Analogicznie obracając układ współrzędnych o kąt φ3 otrzymuję

ω₁l₁sin(φ₁ - φ₃) + ω₂l₂sin(φ₂ - φ₃) + ω₃l₃sin(φ₃ - φ₃) = 0

ω₃l₃sin(φ₃ - φ₃) = 0

ω₂ = -


po podstawieniu danych liczbowych jest

ω₂ = -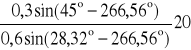
= -7,8 [s^-1]

W celu obliczenia przyspieszeń kątowych różniczkuję równanie (4) przyjmując ω₁ = const

ω₁²l₁cosφ₁ + ω₂²l₂cosφ₂ + ε₂l₂cosφ₂ + ω₃²l₃cosφ3 +ε₃l₃sinφ₃ = 0

Przyspieszenie kątowe członu 3 otrzymuję obracając układ współrzędnych o kąt φ₂

ε₃ = -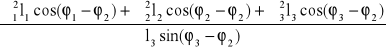


po podstawieniu danych liczbowych jest:

ε₃ = -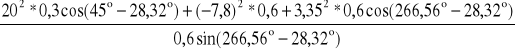


ε₃ = 291,727 [s^-1]

Przyspieszenie kątowe członu 2 otrzymamy obracając układ współrzędnych o kąt φ₃

ε₂ = -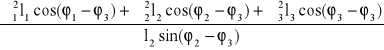


po podstawieniu danych liczbowych jest:

ε₂ = -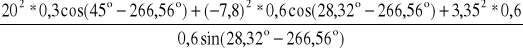


ε₂ = -209,78 [s^-1]

2. PORÓWNANIE WYNIKÓW ANALIZY KINEMATYCZNEJ

		AKM	Met. Wykreślna	Met. analityczna
1 2 3 4 5 6 7 8 9 10	VC VE VS3 ω2 ω3 aC aE aS3 ε2 ε3	3,46 1,07 7,75 189,63 83,24 198,48	2,012 3,4735 1,006 7,8 3,35 175,14 195,26 87,57 203 293,43	- - - 7,8 3,35 - - - 209,78 291,727

• ANALIZA KINETOSTATYCZNA

1. PRZYJĘCIE MAS, MOMĘTÓW BEZWŁADNOŚCI ORAZ SIŁY OPORU

m₃ = 4 [kg]

Is₃ =
=
= 0,12 [kgm²]

Przyjmuję siłę zewnętrzną P₂ = 200 [N]

3.2 OBLICZENIE SIŁ I MOMENTÓW OD SIŁ BEZWŁADNOŚCI




Obliczam siłę bezwładności
oraz moment od sił bezwładności



= -m₃


B₃ = m₃
= 4 * 87,57 = 350,28 [N]


= -I_S3



= I_S3ε₃ = 0,12*291,727 = 35 [Nm]

1. OSWOBODZENIE GRUPY STRUKTURALNEJ OD WIĘZÓW

Podziałka k₁ = 0,01





Równania równowagi sił zewnętrznych i reakcji działających na człony grupy strukturalnej (2, 3)


+
+
+
+
+
= 0

W celu wykreślnego rozwiązania równania należy wyznaczyć składowe styczne:


= 0; -ε
* BC + P₂u = 0


=


Po podstawieniu wartości liczbowych:


=
= 135,62 [N]


= 0; -
* CD - M_B3 + B₃h = 0


=


Po podstawieniu wartości liczbowych


=
= 117,37 [N]

Wykreślne rozwiązanie równania równowagi sił.

Przyjąłem podziałkę k_R = 5



(
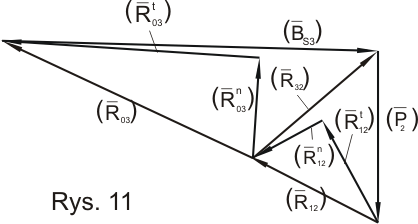
) = 27,124 [mm]

(
) = 23,474 [mm]

(B₃) = 70 [mm]

(P₂) = 40 [mm]

Z rysunku odczytuję:

(R₁₂) = 32,79 [mm]

R₁₂ = 163,95 [N]

(R₀₃) = 64,47 [mm]

R₀₃ = 322,35 [N]

Na podstawie równania równowagi sił dla członu 2 wyznaczam również reakcję R₃₂


+
+
= 0

(
) = 38,38 [mm]


= 191,9 [N]

Analiza sił działających na człon napędzający:


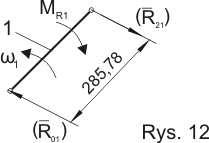
Równania równowagi sił:


+
= 0


= -



= 163,95 * 0,28578


= 55,427 [N]

Obliczenie momentu równoważącego M_R1

M_R1 - R₂₁l₁ = 0

M_R1 = R₂₁l₁

M_R1 = 163,95 * 0,28578 = 55,427031 [Nm]

2. SPRAWDZENIE POPRAWNOŚCI OBLICZEŃ MOMENTU RÓWNOWAŻĄCEGO METODĄ MOCY CHWILOWYCH




M_R1(spr) ω₁ + P₂V_Ecos(α₂) + B₃V_S3cos(α₃) + M_B3 ω₃ = 0

M_R1(spr) = -


Po podstawieniu danych liczbowych

M_R1(spr) = -


M_R1(spr) = -56,5058 [Nm]

Znak (-) momentu równoważącego oznacza, że zwrot jest przeciwny do zwrotu prędkości kątowej członu 1 (jest to moment hamujący). Otrzymana wartość momentu równoważącego w porównaniu z momentem obliczonym na drodze analizy kinetostatycznej wskazuje, że obliczenia zostały wykonane poprawnie.




---