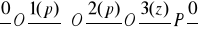AKADEMIA GÓRNICZO - HUTNICZA

w KRAKOWIE

TEORIA MASZYN I MECHANIZMÓW

ANALIZA MECHANIZMU

KORBOWO - SUWAKOWEGO

MECHANIZM 3/A

Wydział Inżynierii Mechanicznej i Robotyki

Rok 2d Rok akademicki 2006/07

Zakres danych	Parametry mechanizmu
1. Struktura mechanizmu.
2. Parametry kinematyczne członu napędzającego.	(φ1, ω1, 0 )
3. Masy i momenty bezwładności członów (mi, Jsi).	(0, 0); (m2, Js2); (0, 0)
4. Obciążenie uogólnionymi siłami zewnętrznymi (Pi, Mi).	(0, 0); (0, M2); (P3, 0)
5. Uogólniona siła równoważąca do wyznaczenia (PR1, MR1).	MR1

Symboliczny zapis struktury i parametrów projektowanego mechanizmu przedstawia następująca tabela:

Mechanizm korbowo - suwakowy.

Rys. 1. Schemat ideowy łańcucha kinematycznego mechanizmu.

1. Analiza strukturalna mechanizmu.

1.1. Ruchliwość i klasa mechanizmu.

Ruchliwość mechanizmu.

,

gdzie:

n - liczba członów;

p₄ - liczba par kinematycznych klasy 4;

p₅ - liczba par kinematycznych klasy 5.

Dla danego mechanizmu:

Klasa mechanizmu.

Po odłączeniu członu napędzającego pozostałe człony (2 i 3) tworzą grupę strukturalną.

Rys. 2. Człon napędzający 1. Rys. 3. Grupa strukturalna (2,3).

Badam ruchliwość grupy strukturalnej po połączeniu jej członów ruchomych z podstawą:

Grupa strukturalna (2,3) jest grupą klasy 2 postaci 2.

1.2. Model mechanizmu w programie SAM.

Dobór parametrów łańcucha kinematycznego.

Rys. 4. Mechanizm w programie SAM.

Człony 2 i 3 z Rys. 4. tworzą w sumie człon 2 z Rys. 1. Dlatego w dalszej części pracy będę się posługiwał oznaczeniami z Rys. 1.

Wymiary mechanizmu i parametry:

Oznaczenia użyte poniżej są wzięte z Rys. 1.

- człon 1 - l_AB = 100 mm = 0,1 m

- człon 2 - l_BC =500 mm = 0,5 m

- człon 3 - l_CD = 100 mm = 0,1 m

- człon 6 - l_FE = 46 mm = 0,046 m

- φ₁ = 0°

- ω₁ = 10 rad/s

2. Analiza kinematyczna mechanizmu.

2.1. Analiza kinematyczna mechanizmu metodą grafoanalityczną.

Rys. 5. Schemat potrzebny do analizy.

W celu rozwiązania zadania metodą grafoanalityczną mechanizm rysuję w podziałce

, gdzie:
- długość rzeczywista członu

- długość rysunkowa członu

w zadanym położeniu. Rysunki zostały wykonane programem AutoCAD. Zadanie zostanie rozwiązane wykreślnie w tym programie, co umożliwi uzyskanie dokładnych wyników.

Analiza prędkości

Analizę prędkości przeprowadzam na podstawie równania: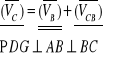
.

Powyższe równanie wektorowe jestem w stanie rozwiązać wykreślnie, metodą planów prędkości.

Przyjmuję podziałkę prędkości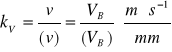
.

.

Rys. 6. Plan prędkości potrzebny do odczytu wartości szukanych.

Odczytuję z rysunku wartości poszczególnych prędkości:

,

.

Dzięki znanej wartości prędkości V­_CB jestem w stanie policzyć wartość prędkości kątowej członu 2 - ω₂:

.

Należy zwrócić uwagę, iż prędkość
.

.

Analiza przyspieszeń

Analizę przyspieszeń przeprowadzamy na podstawie następującego równania:

,

gdzie:
, ponieważ
.

Przyjmuję podziałkę przyspieszeń:

.

.

.

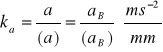
Rys. 8. Plan przyspieszeń do odczytu wartości szukanych.

Odczytuję z rysunku wartości poszczególnych przyspieszeń.

.

.

Mając dane powyższe wartości jestem w stanie obliczyć przyspieszenie kątowe ε₂:

.

Należy także zaznaczyć, że przyspieszenie punktu C będzie równe przyspieszeniu punktu D:

.

2.2. Analiza kinematyczna metodą analityczną.

Wykonuję rysunek wieloboku wektorowego mechanizmu:

Rys. 10. Wielobok wektorowy mechanizmu.

Dane:

l₁ = AB = 0,1m,

l₂ = BC = 0,5 m,

l₃ = 0,1 m,

l₀ = 0,454 m,

φ₁ = φ(t) = 0°,

φ₀ = const = 90°,

φ₄ = const = 180°,

ω₁ = (φ₁)' = 10 [rad/s].

Szukane:

φ₂ , ω₂ , ε₂ , l₄ , V_D , a_D.

Rozwiązanie:

Mechanizm zapisuję wielobokiem wektorowym:

.

Rzutuję na osie wcześniej przyjętego układu współrzędnych powyższe równanie wektorowe, i otrzymuję poniższy układ równań:

.

To:

.

Z drugiego wyznaczam kąt φ₂ :

,

.

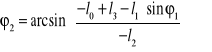
Po podstawieniu danych liczbowych otrzymujemy:

.

Na tej podstawie jestem w stanie wyznaczyć
:

Różniczkuję obustronnie równanie:
,

i otrzymuję: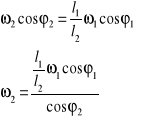

Podstawiając wartości liczbowe, otrzymuję:

.

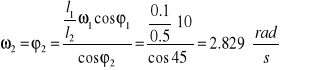
Następnie obliczam przyspieszenie kątowe ε₂ :

Różniczkując obustronnie:

Biorąc pod uwagę, że
i
:

.

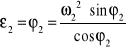
Podstawiając wartości liczbowe:

.

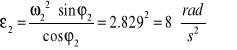
Z drugiego równania wyznaczam l₄ :
.

Różniczkując powyższą zależność otrzymam prędkość punktu D i tym samym C:

.

Podstawiając wartości liczbowe, otrzymuję:

.

Różniczkując ponownie, otrzymuję:

.

2.3. Analiza kinematyczna mechanizmu w programie SAM 4.2.

Wykorzystując zbudowany w programie model mechanizmu wyznaczam wykresy kinematyczne poszukiwanych parametrów kinematycznych w funkcji czasu.

W rozważanym mechanizmie będą to przebiegi:

φ₂ = φ₂(t), ω₂ = ω₂(t), ε₂ = ε₂(t), także: V_D(t), a_D(t).

Rys. 11. Wykres φ₂(t), ω₂(t), ε₂(t).

Rys. 12. Wykres V_D(t), a_D(t).

2.3. Porównanie analizy kinematycznej dla zadanego położenia mechanizmu.

Tab. 1.

Lp.	Parametr	SAM	Metoda grafoanalityczną	Metoda analityczna
1	φ2	45°	-	45°
2	ω2	-2,836		2.829
3	ε2	-7.697	7.96	8
4	VD	1	1	-1
5	aD	15.658	15.62	-15.66

Porównanie wyników obliczeń w powyższej tabeli wskazuje na ich zgodność co oznacza, że nie popełniono błędów obliczeniowych. Duża dokładność metody grafoanalitycznej wynika z zastosowania do wykonania rysunków programu AutoCAD.

3. Analiza kinetostatyczna mechanizmu .

3.1. Przyjęcie mas, momentów bezwładności i sił oporu.

m₂ = 10 kg

J_S2 = 0.5kgm²

P₃ = -100 N

M₂ = 10 Nm.

3.2. Obliczenie sił ciężkości, sił bezwładności i momentów od sił bezwładności.

Aby wyznaczyć siły bezwłodności należy znać przyśpieszenie pkt s2 gdzie odcinek |BS2|=0.25m

Ponieważ ruch punktu
jest ruchem złożonym

,

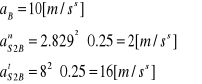
Przyjmuję podziałkę przyspieszeń:

.

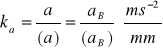
Siła ciężkości członu 2:

Siła bezwładności członu 2:

Moment od siły bezwładności członu 2:

3.3. Wyznaczenie reakcji w parach kinematycznych oraz siły równoważącej metodą grafoanalityczną.

Rysuję mechanizm w podziałce długości - k_l, zaznaczając na rysunku zwroty

przyspieszeń kątowych członów oraz zwrot i kierunek przyspieszenia liniowego środka masy

członu 2. Obciążam mechanizm siłami ciężkości, siłami bezwładności i momentami od sił

bezwładności oraz uogólnionymi siłami zewnętrznymi - oporu:

Rys. 13. Obciążenie mechanizmu.

3.4. Analiza sił działających na grupę strukturalną (2,3).

Uwalniam od więzów grupę strukturalną rozkładając reakcje w przegubach na styczne

i normalne do członów:

Rys. 14. Uwolnienie grupy strukturalnej od więzów.

Zapisuje wektorowe równania równowagi sił działających na człony 2 i 3:

Po dodaniu stronami tych równań otrzymam warunek równowagi sił działających na grupę:

Powyższe równanie posiada trzy niewiadome, jedną z nich (
) można wyznaczyć z równania równowagi momentów dla członu 2.

Równanie równowagi sił działających na grupę przybiera postać:

.

Wykreślam wielobok sił przyjmując następującą podziałkę rysunkową:
.

Rys. 15. Plan sił grupy strukturalnej (2,3).

Na podstawie planu sił odczytuję:

.

3.5. Analiza sił działających na człon napędzający.

Uwalniam od więzów człon napędzający:

Rys. 16. Człon napędzający uwolniony od więzów.

Równanie równowagi sił działających na człon napędzający ma postać:

Rozwiązuję je wykreślnie:

Rys. 17. Plan sił dla członu napędzającego.

Z rysunku odczytuję następujące wartości:

Z równania równowagi momentów działających na człon 1 względem punktu A wyznaczam

moment równoważący:

3.6. Obliczenie momentu równoważącego metodą mocy chwilowych.

Mechanizm rysuję w podziałce kl i obciążam wszystkimi obliczonymi i przyjętymi siłami i

momentami, do członu napędzającego przykładam moment równoważący. Na rysunku zaznaczam

także prędkości liniowe i kątowe w miejscach przyłożenia sił i momentów oraz wartości kątów

pomiędzy wektorami sił i prędkości:

Rys. 18. Schemat do obliczeń metodą mocy chwilowych.

ω2	2.829[rad/s]
ω1	10[rad/s]
VD	-1[m/s]
V	0.707[m/s]

Zapisuję równania mocy chwilowych:

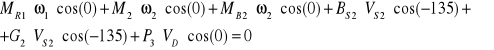
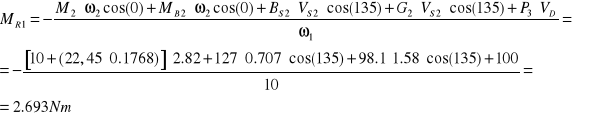
3.7. Wyznaczenie momentu równoważącego w programie SAM.

Buduję model mechanizmu w programie SAM narzucając odpowiednie masy, momenty bezwładności oraz przykładając siłę i moment zewnętrzny:

Rys. 19. Model mechanizmu do analizy kinetostatycznej w programie SAM.

Rys. 20. Charakterystyka momentu równoważącego M_R1(t) w programie SAM.

Dla danego położenia odczytujemy wartość momentu równoważącego:

.

3.8. Porównanie wyników obliczeń momentu równoważącego różnymi metodami.

Metoda grafoanalityczna	Metoda mocy chwilowych	Obliczenia w programie SAM
Nm	Nm	2.455Nm

Z powyższego zestawienia wyników wnioskuję, że obliczenia zostały wykonane poprawnie.

2

---