blabla2, Mechatronika AGH IMIR, rok 2, sprawozdania, TMM

Pobierz cały dokument blabla2.mechatronika.agh.imir.rok.2.doc Rozmiar 899 KB

Fragment dokumentu:

Wydział Inżynierii Mechanicznej i Robotyki

TEORIA MASZYN I MECHANIZMÓW PRECYZYJNYCH

ANALIZA MECHANIZMU 1A

Marcin Matras, grupa 25, Mechatronika

Temat zadania:

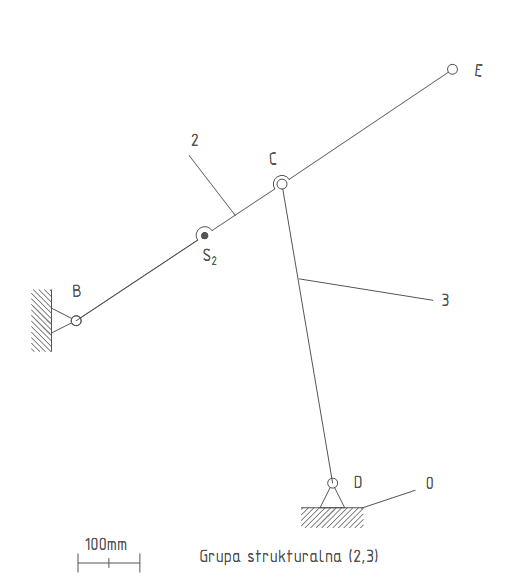
Utworzono mechanizm czworoboku przegubowego zgodnie z zadanym schematem

dane:

m₂=6kg

J_S2=0,5833kg*m²

P₂=150N

M₃=150Nm

=

1. ANALIZA STRUKTURALNA MECHANIZMU

Ruchliwość mechanizmu jest równa 1.

Mechanizm jest klasy V.

n=2

p₅=3

w_gr=0

grupa strukturalna klasy 2

Analizowany łańcuch kinematyczny jest mechanizmem kl. 2

2.ANALIZA KINEMATYCZNA MECHANIZMU METODĄ GRAFOANALITYCZNĄ

Obliczenia:

k_v =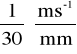
-podziałka prędkości

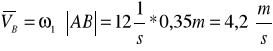
- kierunek wektora prostopadły do |AB|

Obliczam prędkość punktu C:

(1) V_C- ┴ |CD|; V_B- ┴ |AB|; V_CB- ┴ |BC|

(2) V_EB- ┴ |BE|

PLAN PRĘDKOŚCI:

Obliczono prędkości:

V_E= k*( V_E)=2,757 [m/s]

V_C= k*( V_C)=2,033 [m/s]

V_S2= k*( V_S2)=3,024 [m/s]

V_CB= k*( V_CB)=2,97 [m/s]

V_EB= k*( V_EB)=5,77[m/s]

V_S2B= k*( V_S2B)=2,09 [m/s]

Obliczono prędkośc kątowe poszczególnych członówi:

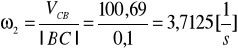
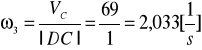
WYZNACZANIE PRZYSPIESZEŃ:

Obliczono a_B, a_C, a_CB:

Równanie przyspieszeń punktu C:

,
║ CD;
┴ CD ;
║ AB;
║ BC ;
┴BC

Z planu odczytano:

Równanie przyspieszenia punktu E:

(3)
║ EB;
┴ EB

Z planu odczytano:

Równanie przyspieszenia punktu S₂:

(3)
║ BC;
┴ BC

Z planu odczytano:

Obliczono przyspieszenia kątowe:

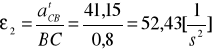
3.ANALIZA KINEMATYCZNA METODĄ ANALITYCZNĄ

3.ANALIZA KINEMATYCZNA PRZY POMOCY PROGRAMU SAM

3.1 Utworzono mechanizm w programie SAM

Pobierz cały dokument blabla2.mechatronika.agh.imir.rok.2.doc rozmiar 899 KB