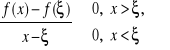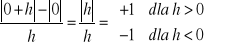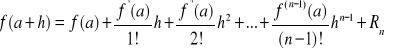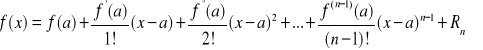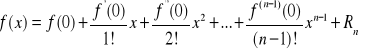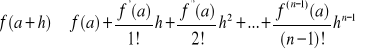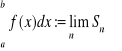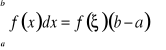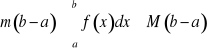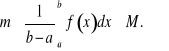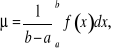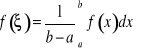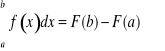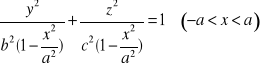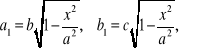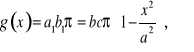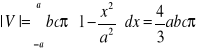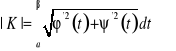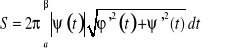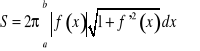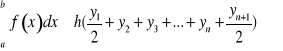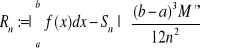Twierdzenie Rolle'a. Jeśli i jest różniczkowalna w oraz , to istnieje taki punkt, w którym . Oznaczamy ten punkt przez i przypuśćmy, że funkcja przyjmuje w nim wartość największą. Wtedy dla wszystkich innych mamy , czyli . Dzieląc tę nierówność obustronnie przez otrzymujemy (1) . Ponieważ funkcja f jest różniczkowalna w , więc przy mamy . Z zależności (1) wynika, że oraz , co jest możliwe tylko wówczas, gdy Twierdzenie (Lagrange'a). Jeśli i jest różniczkowalna w , to istnieje taki punkt , w którym . .Funkcja spełnia wszystkie założenia twierdzenia Rolle'a: jest ciągła i różniczkowalna tam gdzie f oraz . Istnieje wobec tego taki punkt , że oraz . Ale , a więc skąd otrzymujemy tezę twierdzenia. Twierdzenie. Jeśli funkcja jest różniczkowalna w danym punkcie, to jest w nim ciągła. Dowód. Załóżmy, że funkcja f jest różniczkowalna w punkcie x. Wówczas odwrotneRozpatrzmy funkcję . Jej iloraz różnicowy w punkcie wynosi Iloraz ten nie ma granicy gdy , istnieje natomiast granica prawostronna równa 1 i lewostronna równa -1. Funkcja nie ma więc pochodnej w punkcie , ma zaś w tym punkcie pochodną prawostronną równą 1 i lewostronną równą -1.

Różniczka zupełna Jeśli istnieje , to funkcja f posiada różniczkę w a. Jeśli f jest różniczkowalna w a, to przy , skąd Czyli Wniosek. Dla małych h wyrażenie szybko zmierza do 0, skąd dostajemy tzw. przybliżony wzór z różniczką : Twierdzenie (Taylora). Jeżeli w istnieje , to dla każdego istnieje takie c, że gdzie nazywamy resztą Lagrange'a, a c jest nieznanym punktem pośrednim leżącym między . Uwagi. Wzór (9) nazywamy wzorem Taylora. Dla możemy go zapisać w postaci Wzór Taylora w punkcie nazywamy wzorem Maclaurina: Zauważmy, że jeśli wszystkie pochodne są ograniczone przez wspólną stałą i , to mamy . Zatem jest sens opuścić resztę w Dostajemy wówczas tzw. przybliżony wzór Taylora: którego błąd bezwzględny wynosi . Asymptoty Prosta o równaniu jest asymptotą pochyłą w / / krzywej f, jeżeli . jeśli ma miejsce (1.1), to również , czyli . Ponieważ , więc , czyli . Dokładniej: i . i . Twierdzenie ekstremum Jeżeli funkcja ciągła w oraz różniczkowalna w , ma tę własność, że dla i dla / dla i dla /, to ma w punkcie maksimum. Dowód. Z założenia wynika, że funkcja jest rosnąca na lewo, a malejąca na prawo od punktu a, czyli dla oraz dla .Zatem zgodnie z definicją - w punkcie a istnieje max

Twierdzenie (Bolzano Cauchy'ego). Jeżeli oraz , to istnieje taki punkt że Dowód. Załóżmy np., że oraz Dzielimy przedział na połowy. Jeżeli , to dowód jest skończony. Jeżeli tak nie jest, to np. . Wówczas oznaczamy oraz , otrzymując przedział , w którym znowu . Postępujemy z nim podobnie jak z przedziałem i kończymy dowód lub rozpatrujemy tą jego połowę , w której . Otrzymamy w ten sposób ciąg przedziałów , których końce tworzą dwa ciągi: oraz Jeżeli proces ten jest skończony to , można więc przyjąć (KD). Jeśli nie to oba ciągi są nieskończone, monotoniczne i ograniczone, a więc zbieżne, przy czym mają wspólną granicę, bo Niech . Ponieważ funkcja f jest ciągła, mamy . Ale , więc , skąd Twierdzenie (własność Darboux). Jeśli lub , to istnieje taki punkt , że . Dowód. Niech np. . Wprowadzamy funkcję pomocniczą . Funkcja ta jest ciągła oraz i . Zatem spełnia założenia twierdzenia Bolzano-Cauchy'ego. Wobec tego istnieje taki punkt , że czyli Twierdzenie (Weierstrassa). Jeśli to osiąga swe minimum i maksimum w , tzn. istnieją punkty dla których ,

Definicja (całki oznaczonej). Jeśli dla każdego normalnego ciągu podziałów i dowolnie wybranych punktów pośrednich istnieje skończona i ta sama granica , to nazywamy ją całką oznaczoną z funkcji f w przedziale i oznaczamy Twierdzenie (o wartości średniej dla całek). Jeżeli to istnieje w tym przedziale punkt , dla którego . Dowód. Jeżeli m oznacza najmniejszą wartość funkcji w danym przedziale, a M oznacza wartość największą, to , czyli Jeżeli oznaczymy to Stąd wobec ciągłości funkcji i własności Darboux istnieje w przedziale taki punkt , że . Podstawiając za liczbę podaną wartość dostajemy Twierdzenie (zasadnicze rachunku całkowego, związek całki oznaczonej z nieoznaczoną). Jeśli i istnieje funkcja F pierwotna dla f w , to Definicja całki niewłaściwej Niech Punkt b /a/ jest punktem osobliwym tej funkcji, jeśli ( i ) albo /( i ) albo /. Całka nieoznaczona Zbiór wszystkich funkcji pierwotnych dla danej funkcji nazywamy całką nieoznaczoną z f . Całkę nieoznaczoną funkcji oznaczamy symbolem . Zatem Wzory pochodne sinx=2t/1+t2 cosx=(1-t2)/(1+t2) tgx/2=t dx=2/1+t2 dt Sin^2x=t2/1+t2 Cos^2x= 1/1+t2 t=tgx

Obliczyć objętość elipsoidy Powierzchnia elipsoidy ma równanie . Jej przekrój płaszczyzną prostopadłą do osi OX w dowolnym punkcie jest elipsą o równaniu , czyli Ponieważ półosie tej elipsy są równe więc pole przez nią wycięte wynosi przy czym . Szukana objętość jest równa .Dla otrzymujemy kulę, a jej objętość Długość krzywej Niech dana będzie płaska krzywa w postaci parametrycznej . Twierdzenie. Jeżeli , to krzywa K posiada długość . Pole powierzchni obrotowej Jeżeli obracająca się krzywa ma równanie , przy czym , to wzór przyjmuje postać: Przybliżone obliczanie całek oznaczonych - metoda trapezów Metoda trapezów polega na tym, że figurę ABCD zastępujemy figurą złożoną z trapezów wpisanych (rys. 1.59), tzn. krzywą aproksymujemy linią łamaną w nią wpisaną. Przedział całkowania dzielimy przy tym na równe części. Oznaczmy . Wówczas pole figury złożonej z trapezów wynosi , gdzie Stąd otrzymujemy wzór przybliżony w metodzie trapezów: Można pokazać następujące oszacowanie błędu tej metody: , gdzie .

---