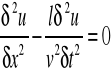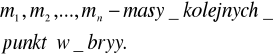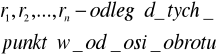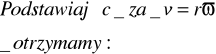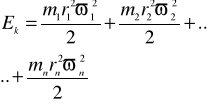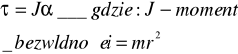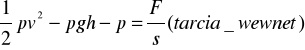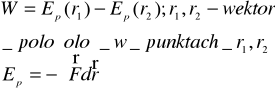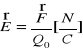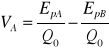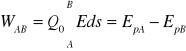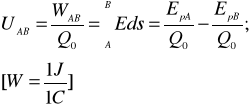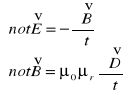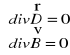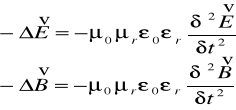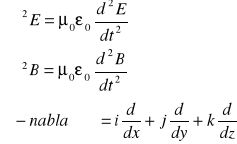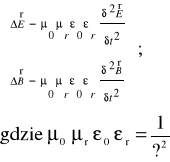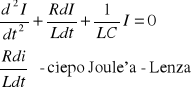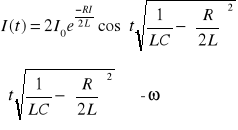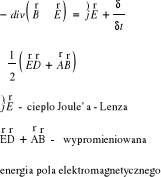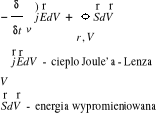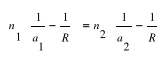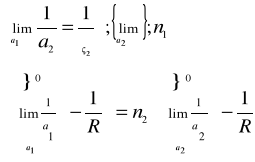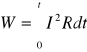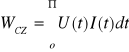RÓWNANIA RUCHU NEWTONA-PRZYKŁADY ZASTOSOWAŃ Newton powiązał przyczyny i skutki ruchu postępowego tworząc 3 zasady dynamiki: I. zasada: porównuje warunki stanu równowagi . "Jeśli na układ nie działa żadna siła lub działające siły równoważą się, to układ pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym”. Układ w którym jest ta zasada spełniona nazywamy inercjalnym. II zasada: wiąże przyczyny i skutki. "Jeżeli na układ działają siły niezrównoważone, to układ ten porusza się z przyśpieszeniem a proporcjonalnym do tej siły; a odwrotnie proporcjonalnym do jego masy." pochodna pędu względem czasu III. zasada: akcji i reakcji "Jeśli na układ pierwszy działa układ drugi, to układ drugi działa na układ pierwszy z tą samą siłą ale przeciwnie skierowaną" FAB FAB Przykłady zastosowań: Punkt materialny wykonuje ruch złożony: Na osi x ruch zmienny: na osi y - ruch jednostajny: ZASADA ZACHOWANIA PĘDU Pęd ciała p jest wektorem równym iloczynowi masy m ciała i jego prędkości v Zasada: "Jeśli wypadkowa sił zewnętrznych (pochodzących od innych ciał)działających na układ ciał jest równa zero, wówczas całkowity pęd układu pozostaje stały mimo działania sił zewnętrznych" Jeżeli w układzie zamkniętym zachodzi zmiana prędkości jednego z ciał układu, to prędkości innych ciał musi się również zmienić tak, aby suma pędów pozostała niezmieniona. Wynika ona z 2 zasad dynamiki, ale jest również ważne to: - w niektórych przypadkach posługiwanie się prawem Newtona może być utrudnione, - jej ogólność wykracza poza normy mechaniki Newtona	ZASADA ZACHOWANIA KRĘTU Kręt, inaczej moment pędu jest wektorem prostopadłym do płaszczyzny, w której leży promień wodzący i pęd i jest skierowany tak jak prędkość kątowa ω Zasada: „Moment pędu ciała, na które nie działają momenty sił, lub momenty te się wzajemnie równoważą jest stały" Jeżeli w układzie zamkniętym jedno z ciał zostanie wprawione w ruch obrotowy pod działaniem sił zewnętrznych to i inne ciała zostaną również wprawione w ruch obrotowy tak aby całkowity moment pędu pozostał bez zmiany. ZASADA ZACHOWANIA ENERGII -Energia jest to zdolność ciała do wykonania pracy. Aby przesunąć ciało z jednego położenia na drugie , lub aby ścisnąć sprężynę należy wykonać pracę. Podczas wykonywania pracy zmieniamy stan ciała. Wielkością opisującą stan ciała jest energia. -Zasada: Energia dowolnego odosobnionego układu fizycznego we wszystkich procesach zachodzących w układzie pozostaje stała przekształcając się przy tym tylko z jednej postaci w inną -Energia zmienia się wtedy, gdy ciało wykonuje pracę. Jeżeli praca ta jest dodatnia to maleje energia potencjalna a wzrasta kinetyczna. Jeżeli praca ujemna to wzrasta energia potencjalna a maleje kinetyczna. CAŁKI RUCHU - ZASADY ZACHOWANIA Siły działające na ciało danego układu można podzielić na: wewnętrzne - działające na dane ciało ze strony innych ciał tego samego układu zewnętrzne - działające na ciało ze strony ciał nie należących do układu Jeśli nie ma sił zewnętrznych to układ nazywamy zamkniętym. W układzie zamkniętym istnieją takie funkcje współrzędnych i prędkości punktów materialnych tworzących układ które zachowują stałą wartość podczas możliwych ruchów układu. Funkcje te nazywamy CAŁKAMI RUCHU. Dla układu złożonego z N cząstek między którymi nie ma sztywnych wiązań można utworzyć 6N=1 całek ruchu. Nas interesują jednak tylko te całki które spełniają addytywności (całka ruchu układu złożonego z podukładów równa jest sumie całek tych podukładów).	Są 3 addytywne całki ruchu: energia pęd kręt (omówione wcześniej). DRGANIA HARMONICZNE PROSTE - SWOBODNE Drgania harmoniczne proste są to drgania odbywające się pod wpływem siły (F)proporcjonalnej do wychylenia (ś) i przeciwnie skierowanej F = - kx . Przyśpieszenie w omawianym ruchu jest proporcjonalne do wychylenia i ma znak przeciwny. Każdy ruch mający taką własność nazywamy harmonicznym. Równanie różniczkowe ruchu harmonicznego wyraża się wzorem: Rozwiązaniem tego równania jest gdzie A i ϕ - wielkości stałe, t- czas Gdy sin(ωt + ϕ) uzyskuje największą wartość =1 to ś również uzyskuje największą wartość = A . Wielkość A nazywamy amplitudą Argument funkcji sin tzn (ωt+ϕ) nazywamy fazą ruchu harmonicznego. Faza jest funkcją czasu (funkcją liniową). ϕ - faza początkowa ruchu. Jej wartość zależy od tego w jakiej chwili zaczęliśmy mierzyć czas. Gdy ϕ= 0 to wzór: A sinωt Wiele przykładów ruchów harmonicznych to wyrażenia jednowymiarowe: - drgania sprężyny - wahadło matematyczne - wahadło fizyczne DRGANIA HARMONICZNE PROSTE - TŁUMIONE W rzeczywistości ze względu na tarcie rozpraszające energię ruchu większość z wymienionych wcześniej ruchów nie ma ustalonej amplitudy. Jeżeli nie doprowadzimy do układu energii drgania stopniowo zanikają ich amplituda maleje i wreszcie układ przechodzi w stan spoczynku. Gdy uwzględnimy istnienie sił tłumiących ruch okresowy nazywamy ruchem harmonicznym tłumionym. Równanie różniczkowe drgań : Różni się ono od równania drgań swobodnych tylko wyrażeniem :	Rozwiązanie równania gdzie A - stała od której zależy pierwsze największe wychylenie, e=2,718 podstawa logarytmu naturalnego Zastępując przez B otrzymamy wzór identyczny jak dla drgań swobodnych z tą różnicą że amplituda B nie jest wielkością stałą a maleje wykładniczo Współczynnik nazywamy współczynnikiem tłumienia. Czas tłumienia jest odwrotnością współczynnika tłumienia RUCH FALOWY - RÓWNANIE FALI Fala mechaniczna - zaburzenia rozchodzące się w przestrzeni ze skończoną prędkością i niosące energię Cechy charakterystyczne fali promień fali powierzchnia fali - miejsce geometryczne punktów fali znajdujących się w tej samej fazie drgań czoło fali - powierzchnia falowa najdalej odsunięta od źródła fali Podział fal -ze względu na ilość wymiarów: --jednowymiarowe, --dwuwymiarowe, --trójwymiarowe. -ze względu na sposób ułożenia na płaszczyźnie: --liniowo(czołem fali jest linia) --kuliste(czołem fali jest okrąg) -ze względu na kierunek rozchodzenia się fali i drgań: --podłużne(rozchodzą się w dowolnych ośrodkach) --poprzeczne(rozchodzą się w ośrodkach sprężystych) Równanie fali: opisuje wychylenie z położenia równowagi punktu w dowolnym czasie: Ogólne rozwiązanie: Równanie fali z transformacją Lorentza.W przestrzeni jednowymiarowej jest ono równaniem różniczkowym. ENERGIA KINETYCZNA W JEDNOSTAJNYM RUCHU BRYŁY SZTYWNEJ. Energia kinetyczna ciała obracającego się dookoła osi równa się sumie energii
kinetycznych jego cząstek. Zatem otrzymaliśmy ostatecznie wzór na energie kinetyczną ciała sztywnego obracającego się dookoła osi: Zatem otrzymaliśmy ostatecznie wzór na energię kinetyczną ciała sztywnego obracającego się dookoła osi: Bryła sztywna-ciało którego poszczególne punkty pozostają w niezmiennej wzajemnej odległości od siebie. Może ona wykonywać 2 rodzaje ruchów: -postępowy—punkty ciała poruszają się po torach równoległych, -obrotowy---punkty ciała zakreślają okrąg współśrodkowy, a ich środki leżą na linii prostej nie biorącej udziału w ruchu zwanej obrotu. MOMENT PĘDU W JEDNOSTAJNYM RUCHU OBROTOWYM BRYŁY SZTYWNEJ Bryła sztywna -(wcześniej).Kręt-moment pędu. Krętem układu punktów lub ciała sztywnego względem osi obrotu będzie suma algebraiczna krętów poszczególn-ych punktów względem tej osi. Dla ciała sztywnego możemy uzyskać prostsze wyrażenie na kręt ,wprowadzając wielkość zwaną prędkością kątową, gdzie i otrzymujemy: ; Teraz zastępujemy fragment poprzez moment bezwładności, otrzymujemy: K = J ω (iloczyn momentu	bezwładności i prędkości kątowej ciała). MOMENT SIŁY W JEDNOSTAJNYM ZMIENNYM RUCHU OBROTOWYM BRYŁY SZTYWNEJ Bryła sztywna(wcześniej) Ruch obrotowy zmienny-ruch taki występuje gdy siła działająca na ciało obracające się wywoła zmianę prędkości kątowej, czyli wystąpi przyspieszenie kątowe. Moment siły względem osi obrotu różny od zera. Zasada: moment siły względem obranej osi obrotu jest równy iloczynowi momentu bezwładności względem tej osi i przyspieszenia kątowego. Przypuśćmy że przykładamy siłę o momencie τ do jednego z punktów ciała sztywnego. Ponieważ wszystkie punkty tego ciała pozostają w ustalonych wzajemnych odległościach, to możemy powiedzieć że przyłożona siła działa na ciało sztywne. RÓWNANIE CIĄGŁOŚCI STRUGI CIECZY, GAZU-POLE WEKTORA PRĘDKOŚCI *Równanie ciągłości : założenie: ciecz jest trakto-wana jako nieściśliwa (р=const) Iloczyn przekroju poprzecznego strugi i prędkości przepły-wu w tym przekroju jest dla danej strugi wielkością stałą. *Pole wektorowe- jest to przestrzeń w której każdemu punktowi przyporządkowano pewną określoną wielkość wektorową *Pole wektora prędkości : uogólnienie równania ciągłości : - pole bezźródłowe: - pole źródłowe : *Własność pola wektora prędkości :Jeżeli natężenie wektora v po dowolnym konturze zamkniętym jest równe zero to pole to jest polem bezwirowym -przepływ cieczy, gazu jest laminarny. W przeciwnym wypadku jest to pole wirowe, a przepływ jest turbulentny. - pole wirowe: =WIRY ≠ 0 pole bezwirowe: = 0	RÓWNANIE BERNOULIEGO DLA STRUGI NIEśCIśLIWEJ CIECZY, GAZU. *Prawo Bernouliego dotyczy przepływu cieczy doskonałej przez przewody o zmiennym przekroju. Wiąże ono ciśnienia i prędkości przepływu na poszczególnych przekrojach z powierzchniami tych przekrojów i ich wysokościami względem obranego poziomu odniesienia. *Prawo Bernouliego : Suma ciśnień (dynamicznego, hydro statycznego i statycznego) jest wielkością stałą dla danej strugi: przypadku gdy ciecz była lepka równanie wygląda następująco: *Zgodnie z prawem przepływuw: -przewężeniach-duża prędkość przepływu i niski ciśnienie -szerokich częściach -mała prędkość przepływu i wysokie ciśnienie *Prawo Bernouliego można również zastosować do gazów, zaniedbując ich ściśliwość gdyż zmiana objętości gazu podczas jego ruchu (prędkości ) jest niewielka. ZASADA TERMODYNAMIKI FENOMENOLOGICZNEJ(OPISOWEJ) Rozważania termodynamiki fenomenologicznej odnoszą się do zjawisk przepływu ciepła (energii) w ośrodkach ciągłych. Są 4 zasady (postulaty): -zerowa zasada termodynamiki: Wszystkie układy fizyczne charakteryzują się widmem energetycznym ograniczonym lewostronnie tzn. każdy układ posiada swój stan równowagi. Konsekwencją tego faktu jest możliwość wprowadzenia parametru porównawczego zwanego temperaturą bezwzględną. -pierwsza zasada termodynamik: Ciepło dostarczone do układu powoduje zmianę energii wewnętrznej (wzrost) układu i pracę wykonaną przez ten układ na Ciepło - suma wszystkich rodzajów energii kinetycznych cząsteczek Energia wewnętrzna - suma wszystkich rodzajów energii kinetycznych cząstek i wszystkich energii potencjalnych oddziaływań cząstek.	DRUGA ZASADA TERMODYNAMIKI: Pracę mechaniczną można zamienić w każdych warunkach na ciepło, ale nie odwrotnie. Zamiana ciepła na pracę w silniku termodynamicznym jest możliwa jedynie wtedy, gdy źródło dostarczające ciepło ma temperaturę wyższą od najzimniejszego ciała w jego otoczeniu. Niemożliwa jest konstrukcja perpetum mobile drugiego rodzaju (nieskończone działanie po jednorazowym dostarczeniu energii). TRZECIA ZASADA TERMODYNAMIKI: Wszystkie potencjały termodynamiczne (entropia) ciał stałych i ciekłych przy temperaturze zmierzającej do 0°K (temp. zera bezwzględnego) zmierzają do zera, czyli są wielkościami bezwzględnymi. II-GA ZASADA TERMODYNAMIKI _ ASPEKT PROBABILISTYCZNY (ENTROPIA BOLTZMANA. PRAWO WZROSTU ENTROPII) -II-ga zasad termodynamiki - (wcześniej - paragraf 14) -Entropia - to funkcja stanu charakteryzująca kierunek przebiegu spontanicznych procesów w odosobnionym układzie termodynamicznym. Zmiana entropii ΔS odpowiadająca przejściu odwracalnemu od stanu 1 do 2 wyraża się wzorem: , a równocześnie -Entropia Boltzmana , gdzie k - stała Boltzmana , P - prawdo podobieństwo termodynamiczne (P≥1) Zmiana entropii Boltzmana w procesach odwracalnych: - entropia się zmienia Zmiana entropii Boltzmana w procesach nieodwracalnych: - entropia się wzrasta Tak więc w termodynamice fenemologicznej tkwi warunek probablistyczny (prawdopodob.). Wynika to z entropii Boltzmana. Jest to specyficzny rachunek prawdopodobieństwa oparty na prawdopodobieństwie termodynamicznym (P≥1) - Prawo wzrostu entropii
Wzrost entropii w parze wraz z przejściem układu do stanu mniejszego uporządkowania cząsteczek. Przejęciu układu do stanu większego chaosu towarzyszy degradacja energii, gdyż układ samorzutnie nie wraca do stanu bardziej uporządkowanego, czyli mniej prawdopodobnego. ROZKŁAD MAXWELLA - WARTOŚĆ ŚREDNIA PRĘDKOŚCI . KWADR. PRĘDKOŚCI. ENERGII - W gazie nie ma żadnego wyróżnionego kierunku prędkości. Wszystkie kierunki prędkości są równie prawdopodobne. Inaczej przedstawia się sprawa różnych wartości prędkości. Prawo rozkładu prędkości Maxwella właśnie tego dotyczy. - Cząsteczki gazu mają wartości prędkości, od bardzo małych, bliskich zeru, do bardzo dużych. Informacja wyciągnięta z rozkładu mówi nam, że pewnej określonej wartości prędkości odpowiada największa liczba cząstek. Jest to tzw. prędkość najbardziej prawdopodobna. Sumując wartości liczbowe prędkości wszystkich cząsteczek i dzieląc wynik przez liczbę cząsteczek V znajdujemy tzw. prędkość średnią Prędkość średnia nie jest równa prędkości najbardziej prawdopodobnej. Przeważają cząstki o prędkościach większych od najbardziej prawdopodobnej. - Wzór na rozkład Maxwella: - dla 1 stopnia swobody: - dla 2 stopnia swobody: - dla S stopnia swobody: jest to funkcja S zmiennych: ROZKŁADY BOLTZMANA. MAXWELLA - BOLTZMANA - Klasyczne (niekwantowe) funkcje rozkładu: - funkcja rozkładu Maxwella:	- funkcja rozkładu Boltzmana: - energia potencjalna oddziaływań cząstek zewnętrznym polem, mogą to być również efektywne energie potencjalne, wiązane z wzajemnym oddziaływaniem B - norma rozkładu funkcji Boltzmana: - funkcja rozkładu Maxwella-Boltzmana: ,gdzie A - normalna funkcji tego rozkładu: Rozkład Maxwella - Boltzmana daje dobre wyniki tylko w przypadku gazów atomowych (szlachetnych, doskonałych) w wysokich temperaturach, tzn. dotąd, dokąd nie ujawniają się efekty kwantowo - mechaniczne. W przypadku gazów i par o cząsteczkach dwuelementowych otrzymane wyniki są dostatecznie dobre i stosujemy wtedy funkcję rozkładu Maxwella dla S stopnia swobody. Gazy i pary trójelementowe - dla S stopnia swobody. CZY ZAWSZE JEST SPEŁNIONA ZASADA EKWIPARTYCJI ENERGII (ROZKŁADY KWANTOWE FERMIEGO-DIRACA I BOSEGO-EINSTEINA) - Zasada ekwipartycji energii wynikająca z mechaniki klasycznej słuszna jest jedynie w dostatecznie wysokich temperaturach. Mechanika kwantowa, której przybliżeniem jest mechanika klasyczna, prowadzi do wniosku, że w pewnych warunkach określony sens nadać można i ujemnym temperaturom bezwzględnym. Mechanika kwantowa wskazuje również, że zasada ekwipartycji energii (warunkiem równowagi jest ustalenie się temperatury gazu) w niskich temperaturach przestaje być słuszna. Bezpośrednim wnioskiem z zasady ekwipartycji energii jest to, że temperatura jest wielkością statyczną. O temperaturze gazu możemy więc mówić tylko wtedy, gdy mamy do czynienia z	bardzo wieloma cząsteczkami gazu, a w przeciwnym wypadku, tj. gdy liczba cząsteczek jest bardzo mała, temperatura gazu jest właściwie wielkością nieokreśloną. - Opis klasyczny można stosować dotąd, dokąd spełniona jest zasada ekwipartycji energii (równego rozkładu energii). Z chwilą, gdy przestaje ona być spełniona należy kwantowo-mechaniczne funkcje rozkładu: - funkcja rozkładu Bosego-Einsteina , gdzie cząstkę cząstkę Ta funkcja rozkładu jest stosowana do cząstek zwanych bosonami, cząstek o spinie całkowitym nie podlegającym prawom Pauliego, który orzeka, że w jednym stanie kwantowym może się znajdować najwyżej jedna cząstka o spinie połówkowym. - funkcja rozkładu Fermiego-Diraca Stosujemy do cząstek o spinie połówkowym, podlegających zakazowi Pauliego. - Ogólnie: δ = -1 (Bosego-Einsteina) δ = 0 (Maxwella - Boltzmana) δ = 1 (Fermiego-Diraca) POLE GRAWITACYJNE-WŁASNOŚCI. *Na ciało umieszczone w skończonej odległości od innego ciała działa siła grawitacji (ciężkości), a wytworzone przez to ciało pole nazywamy polem grawitacyjnym. *Określniki pola grawitacyjnego: -Natężeniem pola grawitacyjnego w danym punkcie nazywamy stosunek siły grawitacji działającej na znajdujący się tam punkt materialny do masy tego punktu. - Linia pola grawitacyjnego-jeśli w pole grawitacyjne wprowadzimy punkt materialny i pozwolimy mu poruszać się w tę stronę, w którą działa siła grawitacji, to zakreśli on tor zwany linią pola grawitacyjnego. - praca - Pole grawitacyjne jest polem zachowawczym tzn. że praca wykonana przez siły pola przy pełnym obiegu po dowolnej krzywej zamkniętej jest równa zero. Praca w polu grawitacyjnym nie zależy od punktu początkowego	i końcowego(cecha pola zachowawczego), - Energia potencjalna Ep - jest to funkcja, dzięki której pracę sił pola zachowawczego można pokazać jako różnicę wartości tej funkcji. - potencjał grawitacyjny V -stosunek energii potencjalnej punktu materialnego, umieszczonego w danym punkcie pola, do jego masy, -Powierzchnia ekwipotencjalna -zbiór punktów o tej samej wartości potencjału Gradient-spadek; największa wartość pochodnej kierunku - Prawo powszechnej grawitacji- wartość siły grawitacyjnej jest wprost proporcjonalna do iloczynu mas punktów materialnych, a odwrotnie proporcjonalna do kwadratu odległości pomiędzy nimi, RUCH POD WPŁYWEM SIŁY CENTRALNEJ - PRAWA KEPLERA. *W centralnym polu grawitacyjnym, którego centrum stanowi nieruchome ciało o masie M znajdujące się w początku układu, wektor natężenia pola grawitacyjnego ma postać: gdzie G- stała grawitacji, M- całkowita masa bryły, F- siła grawitacyjna Punkt materialny, na który działa tylko siła centralna(zawsze przechodzi przez centrum ruchu), porusza się stale w jednej płaszczyźnie, w której leży centrum pola. Ruch pod wpływem siły centralnej jest ruchem płaskim. *Prawa Keplera: - I prawo-punkt materialny w centralnym polu grawitacyjnym może poruszać się tylko po krzywych stożkowych(elipsach, parabolach, hiperbolach), których ogniskiem jest centrum pola oraz po prostych przechodzących przez centrum pola. - II prawo-promień wodzący planety zakreśla równe pola w równych odstępach czasu; inaczej: prędkość polowa punktu materialnego w układzie odniesienia o początku w centrum pola jest stała.
-III prawo- stosunek kwadratu okresu T obiegu planety dookoła Słońca do sześcianu średniej odległości R od niego jest dla wszystkich planet układu słonecznego jednakowy POLE ELEKTRO STATYCZNE-RÓWNANIA ELEKTROSTATYKI. *Ładunek elektryczny wywołuje w swoim otoczeniu pewne zmiany, objawiające się w ten sposób, że inny ładunek wprowadzony do tego obszaru polega działaniu sił kolumbowskich (ładunek wytwarza wokół siebie pole elektryczne). Jeżeli siła działająca na ładunek próbny w danym punkcie pola nie ulega zmianie, mówimy o polu elektrostatycznym gdzie: E- natężenie pola elektrycznego, F - siła działająca na ładunek próbny, - wartość ładunku próbnego. Uwzględniając prawo COULOMBA: *Własności pola: - potencjał elektryczny danego punktu pola - praca jaką muszą wykonać siły pola aby ładunek jednego kulomba przenieść z jednego punktu do punktu nieskończenie odległego: -potencjał punktu A,-energia potencjalna, -wartość ładunku próbnego. - praca przenoszenia ładunku w polu: - napięcie elektryczne : *Równanie elektrostatyki: I równanie: pole elektryczne jest polem źródłowym: Ii równanie: pole elektryczne jest polem bezwirowym:	(krążenie wektora pola elektrycznego po dowolnym konturze). KONDENSATORY-POJEMNOŚĆ ELEKTRYCZNA *Kondensator- przyrząd służący do gromadzenia ładunków elektrycznych i stanowiący układ przewodników o określonej pojemności elektrycznej. Schemat zastępczy: Budowa: dwie płytki (okładki) rozdzielone izolatorem. *Pojemność elektryczna - C - stosunek ładunku Q zgromadzonego na przewodniku do napięcia będącego różnicą potencjałów między przewodnikiem a otoczeniem *łączenie kondensatorów - szeregowe Mikro i makroskopowa postać prawa Ohma. - Mikroskopowa- tzn. ze określa zależność dla każdego punktu ciała. R = ρ * l / s gdzie R - opór J = I / S ρ - opór właściwy materiału przewodnika J = η E l -długość przewodnika η = l / ρ S -powierzchnia przekroju poprzecznego ρ = S R / l j - gęstość prądu I - natężenie prądu - Makroskopowa- tzn. ze odnosi się do konkretnego ciała albo jego określonej części. R = U / I gdzie R - opór U - napięcie I - natężenie Natężenie prądu stałego I płynącego przez przewodnik jest wprost proporcjonalne do natężenia elektrycznego U występującego miedzy końcami przewodnika a odwrotnie proporcjonalne do jego rezystancji R. Mikro i makroskopowa postać ciepła Joule`a-Lenza. Mikroskopowa: W = j E + ( S. L ) = j E + Vobj (j = I / S -gęstość prądu) Makroskopowa: W = U * I ^ 2 * t (W = q U , a q = J * t , wiec W = U * I ^ 2 * t ) Ilość ciepła wydzielonego w	wyniku przepływu prądu przez przewodnik jest wprost proporcjonalna do natężenia tego prądu ,czasu jego przepływu i spadku napięcia na końcach tego przewodnika. Prawa Kirchoffa I prawo: Suma prądów dopływających do dowolnego węzła obwodu elektrycznego jest równa sumie prądów odpływających od węzła.(węzeł - dowolny punkt w którym schodzą się . więcej niż 2 przewody) I 1+I2=I3+I4 II prawo W dowolnym oczku obwodu elektrycznego prądu stałego suma spadków napiec na elementach rezystancyjnych oczka jest równa algebraicznej sumie działających w tym oczku sil elektromotorycznych(napiec) (oczko- zbiór gałęzi obwodu ,który tworzy w obwodzie drogę zamknięta) Vb-Va)+ +(Va -Vc)+(Vc-Vb)=0 (suma napiec w oczku bacb Energia kondensatora -Energia pola elektrycznego Energia kondensatora :jest to praca jaka wykonaliśmy magazynując na kondensatorze ładunek Q. C=Q/U , wiec podstawiając za Q=C*U otrzymujemy: , gdzie , a to oznacza ze energia pola elektrycznego miedzy okładkami kondensatora = energii kondensatora czyli pracy z jaka gromadzi on ładunek Q. Q = C*U, wiec	Kondensator przechowuje w sobie elektryczna energie potencjalna rowna pracy niezbednej do naladowania go. SiłyLorentza,Ampere'a-określeniepolamagnetycznego pole magnetyczne - przestrzeń w której na poruszające się ładunki elektryczne albo pewne ciała nieruchome działają określone siły. Pole magnetyczne jest siedliskiem energii. Określniki: - wektor indukcji magnetycznej - definicja tego wektora oparta jest na prawie Ampere'a, które określa się oddziaływania d·F pola magnetycznego na element prądu (iloczyn natężenia prądu I przez element długości przewodnika liniowego w którym płynie prąd). Siłę działającą na element przewodnika z prądem umieszczonego w zewnętrznym polu magnetycznym nazywamy siłą elektrodynamiczną. Wielkość tej siły jako wektora określa prawo Ampere'a. ; gdzie: I - natężenie prądu, B - wektor indukcji magnetycznej [T]. - wektor natężenia pola magnetycznego - związany jest z indukcją magnetyczną zależnością: ; - bezwzględna przenikalność magnetyczna substan. - strumień magnetyczny gdzie: - strumień powierzchniowy, - kąt pomiędzy wektorem normalnym do tego elementu pola i kierunkiem wektora. - siła Lorentza - Jeżeli naładowana cząstka q porusza się w obszarze, w którym istnieje zarówno pole magnetyczne jak i elektryczne, siłę wypadkową działającą na tę cząstkę (siłę Lorentza) otrzymujemy z równań: 1.(pole elektryczne) 2. F=qVB (pole magnetyczne) Siła Lorentza: F=qE+qVB Pole magnetyczne przewodników z prądem - wzór Biote'a - Savarta. Igła magnetyczna ustawiona w pobliżu przewodu np. równolegle do niego, zmienia natychmiast kierunek ustawienia gdy tylko
przez przewód przepuścimy prąd elektryczny. Dzieje się tak dlatego, że w otoczeniu przewodu powstaje pole magnetyczne. Linie tego pola wokół przewodnika prostoliniowego są kołami współśrodkowymi, których środki leżą na osi przewodu. W wielu przypadkach możemy obliczyć natężenie pola posługując się prawem Erote'a - Savarta, które określa w ustalonym punkcie przestrzeni P indukcję pola magnetycznego sB przechodzącą od elementu przewodnika dl, przez który przepływa prąd o natężeniu I: gdzie: r - wektor skierowany od elementu dl do punktu P. - przenikalność magnetyczna próżni. Przykładem zastosowania tego prawa jest obliczenie indukcji pola w środku kołowego przewodnika z prądem, ponieważ dl i r są do siebie prostopadłe to wzór wygląda: ; gdzie: r - promień kołowej wiązki Prawo indukcji Faradaya - indukcja własna i wzajemna. Prawo indukcji - Siła elektromotoryczna (SEM) indukcji powstająca w obwodzie elektrycznym pod wpływem zmian strumienia pola magnetycznego, jest proporcjonalna do szybkości zmian strumienia indukcji magnetycznej przenikającego dowolną powierzchnię ...?... tym obwodem:. Zmiany strumienia mogą być spowodowane przez ruch obwodu względem pola magnetycznego przez sąsiedni obwód, w którym płynie prąd lub przez zmianę kształtu pola poza obwodem. Indukcja własna - jest to zjawisko indukowania się siły elektromotorycznej w przewodzie pod wpływem zmian prądu płynącego przez niego. Siłę tę - siłę samoindukcji wyrażamy wzorem: .	Siła elektromotoryczna indukcji własnej nadaje prądowi cechę bezwładności, przeciwdziała wszelkim zmianom prądu w obwodzie. Wykorzystuje się ją w autotransformatorach. Indukcja wzajemna - jest to zjawisko indukowania się siły elektromotorycznej w przewodzie pod wpływem zmian prądu w innym przewodzie z nim sprzężonym. Wzór wygląda następująco: . Zjawisko to wykorzystuje się w budowie transformatorów. Indukcja elektromagnetyczna - prąd zmienny. W cewce obracającej się ruchem jednostajnym w polu magnetycznym jednorodnym powstaje siła elektromotoryczna dana wzorem: . Wzór ten jest identyczny z wzorem na ruch harmoniczny. Wychylenie jest to chwilowa wartość siły elektromotorycznej Em , amplituda to maksymalna wartość siły elektromotorycznej E0. Gdy w obwodzie działa siła elektromotoryczna sinusoidalnie zmienna, płynie w nim prąd również sinusoidalnie zmienny, zwany po prostu prądem zmiennym. Chwilowe natężenie tego prądu dane jest wzorem: . Między siłą elektromotoryczną a natężeniem prądu istnieje różnica faz. Jeżeli ramka wiruje w polu magnetycznym to siła elektromotoryczna w niej wynosi: . Skuteczna wartość prądu zmiennego nazywamy wartość natężenia prądu stałego wykonującego w takim samym czasie taką samą pracę jak prąd zmienny (np. przy zamianie na ciepło). Równanie Maxwella -równanie falowe dla pól Ei B Zakładamy, że będziemy rozwiązywać pola elektromagnetyczne w próżni (brak ładunku) ^gęstość prądu ^ ^prąd^	ostatecznie: równanie falowe dla pól E i B w przestrzeni trójwymiarowej • Wnioski: równania Maxwella zawierają w sobie ograniczone równania falowe na wektory E i B równania Maxwella - jak równania falowe - są niezmienne względem transformacji Lorentza równania Maxwella w interpretacji szczególnej teorii względności zasługują na miano praw fizyki Drganiaw obwodzie szeregowo połączonych R,L,C Obwód drgający jest to obwód, w którym może występować rezonans elektryczny (oscylacja prądu), charakteryzująca się okresową wymianą energii w naładowanym kondensatorze na energię prądu elektrycznego w cewce. Najprostsze obwody drgające rezonansowe to układy złożone z rezystancji R, pojemności C i indukcyjności L w połączeniu szeregowym lub równoległym. obwód szeregowy Zależność impedancji Z obwodu szeregowego od częstotliwości kątowej ω doprowadzonego napięcia jest określona wzorem: Gdy R ≈ 0 drgania w obwodzie są harmoniczne (ładunek, napięcie i natężenie zależą sinusoidalnie):	Wzór Thompsona-Kelvina: drgania własne W takim obwodzie gdy R = 0 straty energii odbywają sie przez wyemitowanie pól magnetycznego i elektrycznego . R ≠ 0 - tak jest w obwodach rzeczywistych (oporność uzwojenia cewki i przewodów). Oporność tej części energii i drgań zmienia się na ciepło i całkowita energia drgań maleje w miarę upływu czasu. Nazywamy je drganiami własnymi tłumionymi. drganiu tłumione Równania Maxwella - interpretacja. Równania Maxwella są to równania ujmujące matematycznie teorię pola elektromagnetycznego. Są 4 takie równania: I równanie: Wokół każdego ładunku elektrycznego rozciąga się obszar pola elektrycznego o natężeniu : (z prawa Gaussa dla elektryczności) „Zmienne pole magnetyczne wywołuje wirowe pole elektryczne” II równanie: Wokół przewodnika z prądem istnieje pole magnetyczne o indukcji magnetycznej , lecz nie istnieją ładunki elektryczne podobne do elektrycznych. (z prawa Gaussa dla magnetyzmu)
„Składowa elektryczna jest źródłowa” III równanie: Prąd I wytwarza wokół przewodnika, w którym płynie prąd, pole magnetyczne o natężeniu B: (z prawa Ampere'a) ^wiry pola magnet.^ „Zmienne pole elektryczne generuje wirowe pole magnetyczne” IV równanie: Zmieniające się pole magnetyczne wytwarza w przewodniku siłę elektromotoryczną: (z prawa Faradaya) „Składowa magnetyczna jest bezźródłowa” Interpretacja: I równanie: Dotyczy ładunku i pola elektrycznego. Ładunek umieszczony w izolowanym przewodniku przemieszcza się w kierunku jego powierzchni zewnętrznej. II równanie: Dotyczy pola magnetycznego. Nie można utworzyć pojedynczego odosobnionego bieguna magnetycznego. III równanie: Dotyczy efektu magnetycznego zmieniającego się pola elektrycznego lub prądu. Prędkość światła można wyliczyć z pomiarów czysto elektromagnetycznych. Prąd płynący w przewodniku wytwarza wokół siebie pole magnetyczne. IV równanie: Dotyczy efektu elektrycznego zmieniającego się pola magnetycznego. Magnes płaski przesuwany przez zamknięty obwód powoduje powstanie w nim prądu. ZASADA ZACHOWANIA ENERGII DLA POLA ELEKTROMAGNETYCZNEGO - WEKTOR POVTINGA • Założenia: rozważamy pole elektromagnetyczne w próżni p=0 i j=0 μr εr =CONST • Zasada zachowania energii - sformułowanie różniczkowe:	• Zasada zachowania energii - postać ostateczna: • Wektor Poytinga (S=1/μc*E×B) - określa prędkość przepływu energii dla fali. Jest to ilość energii przechodzącej w ciągu jednostki czasu przez jednostkową powierzchnię prostopadłą do kierunku tego wektora S • Wniosek : jawne sformułowanie zasady: „Ubytek energii pola elektromagnetycznego spowodowany jest wydzieleniem się ciepła Joule'a - Lenza i energii wypromieniowanej z obwodu”. NIEZMIENNIK ZEROWY ABBY'EGO DLA DIOPTRII SFERYCZNEJ • Dla dioptrii sferycznej zachowana jest zasada niezmiennika Abby'ego: n - współczynnik załamania R - promień krzywizny • Dla lewego ośrodka n1(1/a1 - 1/R) Dla prawego ośrodka n2(1/a2 - 1/R) Niezmiennik dla dioptrii sferycznej:	ZASADA FERMATA - PRAWA ODBICIA ZAŁAMANIA • Zasada Fermata - rzeczywista droga optyczna jaką przebywa promień świetlny między dwoma punktami jest najkrótsza spośród wszystkich możliwych dróg optycznych między tymi punktami Z zasady tej sformułujemy prawo odbicia i załamania światła. • Prawo odbicia: odbicie - skokowa zmiana kierunku rozchodzenia się promienia padającego, co następuje na dostatecznie głębokiej powierzchni dzielącej dwa ośrodki, w których prędkości rozchodzenia się światła są różna prawa odbicia - promień padający i odbity leżą w jednej płaszczyźnie kąt padania równa się kątowi odbicia α = α' • Prawo załamania: załamanie - gdy promień pada na powierzchnię rozdzielającą dwa ośrodki, część promienia padającego odbija się a część przechodzi do drugiego ośrodka, przy czym kierunek promienia zmienia się nagle na powierzchni prawa załamania - promień padający i załamujący leżą w jednej płaszczyźnie dla dwóch danych ośrodków sinusy kątów padania i załamania są proporcjonalne: sinβ ≅ sinα względny współczynnik załamania światła (n): sinα/sinβ=n i n=V1/V2 α - kąt padania β - kąt załamania Równanie zwierciadeł (Z niezmiennika zerowego Abbe'go) Zwierciadło optyczne - powierzchnia odbijająca o współczynniku odbicia światła bliskim jedności. Wykonuje się	je z metalu lub szkła pokrytego warstwą odbijającą. Rozróżnia się zwierciadła: - płaskie | - wklęsłe ) - wypukłe ( Równanie zwierciadeł: gdzie: x,y - odległość przedmiotu i obrazu od zwierciadła (x>0 i y>0 gdy obraz rzeczywisty) f - ogniskowa Równanie soczewek (Z niezmiennika zerowego Abbe'go) Soczewka - przeźroczyste ciało jednorodne ograniczone dwiema zakrzywionymi powierzchniami o promieniach R1 i R2 Ze względu na działanie soczewki dzielimy na skupiające i rozpraszające. Ze względu na budowę na: - dwuwypukłe () - płasko-wklęsłe |_( - płasko-wypukłe |_) - dwuwklęsłe ) ( Równanie soczewek: gdzie: x,y - odległość przedmiotu i obrazu od zwierciadła lub gdzie: D - zdolność skupiająca soczewki, n - współczynnik załamania soczewki; R1 - promień krzywizny pierwszej (od przedmiotu); R2 - promień krzywizny drugiej (od obrazu) Interferencja (Otrzymanie wiązki monochromatycznych Koherentnych) Interferencja - nakładanie się dwóch lub więcej wiązek światła w tym samym obszarze, w wyniku czego wiązki lokalne wzmacniają się lub osłabiają (gdy dwie fale świetlne mają tory zgodne - następuje wzmocnienie; gdy tory są przeciwne - osłabienie) Wiązka monochromatyczna koherentna - wiązka o jednej długości fali i różnica faz pozostaje stała w czasie. Światło spójne - laserowe (spójne = koherentne) Aby uzyskać wiązkę monochromatyczną koherentną, należy przeprowadzić doświadczenie: 1) umieszczamy dwa źródła światła, które wysyłają światło spójne, od szczeliny w odległości y
2) szczelina o szerokości d spełnia role światła spójnego i wydziela nową wiązkę światła 3) musi być spełniony warunek zwany warunkiem spójności źródła światła λ - długość fali Dyfrakcja - wzór Bragga dla siatki dyfrakcyjnej liniowej dyfrakcja - zjawisko polegające na uginaniu się promieni świetlnych siatka dyfrakcyjna - układ równoodległych szczelin, rozmieszczonych w równych odstępach wzór Bragga - wzór określający położenia maksimów natężenia promieniowania rentgenowskiego, ulegającego dyfrakcji w wyniku padania na kryształ. Maksimum dyfrakcyjne równoodległej, monochromatycznej wiązki promieni X o długości fali λ padającej na układ płaszczyzn sieciowych w ten sposób, że tworzą z nimi kąt θ, przy spełnieniu warunku zwanego wzorem Bragga: 2 d sin θ = n λ ; n - liczba całkowita oznaczająca kąt odbicia θ - kąt Bragga, d - odległość między równoległymi płaszczyznami. Wiązka ugięta rozchodzi się przy tym tak, jak gdyby uległa odbiciu (zwanego odbiciem Braggowskim) od płaszczyzny równoległej do płaszczyzn siecznych, a więc też tworzy z nimi kąt θ. Pole elektryczne o symetrii sferycznej ładunku punktowego V>>R 1) z prawa elektr. 2) czyli 3) powierzchnia zr sfery o promieniu r jest powierzchnią ekwiskalarną, tzn. taką na której wartości wielkości polowych są stałe: rΛD = const	(wektor indukcji) (wektor natężenia pola elektrycznego) (siła) (potencjał pola) 4) W punkcie, w którym ładunek się znajduje „?” w jego pobliżu pole jest nie określone; jest określone dla r = ∞ 5) Pole to jest polem Culombowskim. Pole elektryczne o symetrii sferycznej wewnątrz sferycznej chmury ładunków o gęstości ładunków=const. czyli jestpowierzchnią ekwiskalarnaD=constna Nie jest to pole Culombowskie ; ; ; V(r)-V(0)= Pole elektryczne o symetrii osiowej wytworzone przez jednorodnie naładowany cienki przewód. Nie jest to pole Culombowskie Z prawa elektr. I na na b powierzchnia ekwiskalarna, czyli D=const na . ; ; V(R)-V(0)= pole to jest nie określone w	r=0 I r→∞ zmierzają do 0) Zjawisko fotoelektryczne - kwantowa natura fali elektromagnetycznej. Nie wszystkie zjawiska optyczne można wytłumaczyć na gruncie falowej teorii światła. Badania zjawiska fotoelektrycznego dowodzą, że światło monochromatyczne padające na płytkę metalową zwaną fotokatodą, wyrywa z niej elektrony zwane fotoelektronami. Fotoelektrony przyspieszane przez pole elektryczne powstałe dzięki dodatniemu względem katody potencjałowi anody, wytwarzają w obwodzie prąd elektryczny. Trzy zasadnicze cechy zjawiska fotoelektrycznego nie dadzą się wyjaśnić za pomocą teorii falowej, z której wynika, że: Energia kinetyczna fotoelektronu powinna wzrastać wraz z natężeniem światła, czego się nie obserwuje; Efekt ten powinien występować dla dowolnej częstotliwości v światła przy odpowiednio dużym natężeniu, co nie zachodzi; Gdy światło jest dostatecznie słabe, elektrony wybijane z katody powinny (wg. Teorii falowej) wykazywać charakterystyczne opóźnienie w czasie w stosunku do początku naświetlania katody, czego również się nie obserwuje. Albert Einstein wyjaśnił efekt fotoelektryczny w sposób bardzo prosty, dzięki założeniu, że wiązka światła rozchodzi się w przestrzeni w postaci tzw. fotonów, z których każdy wynosi porcję energii - kwant E=hv. W ramach tej koncepcji zjawisko fotoelektryczne można wyjaśnić za pomocą własności Einsteina. Hv=E0-Ek MAX energia hv=E dostarczona przez foton przenikający warstwę powierzchniową fotokatody zostaje zużyta na przejęcie elektronu przez warstwę metalu. Jest to praca wyjścia E0 . przepisując inaczej równanie Einseina mamy liniowy związek między potencjałem hamującym V0, a częstotliwością v światła. Opisane zjawisko to zewnętrzne zjawisko fotoelektryczne. Zjawisko Camptona - kwantowa natura fali elektromagnetycznej. Zjawisko Camptonato doświadczalne potwierdzenie istnienia fotonu jako skończonej porcji energii. Zjawisko to, jest	rozpraszaniem promieniowania elektromagnetycznego (gł. Roentgenowskiego) na swobodnych elektronach, któremu towarzyszy zwiększanie długości fali promieniowania I odrzut elektronu. Wiązkę promieni roentgena o dokładnie określonej długości fali kierował Campton na blok granitowy oraz mierzył dla różnych kątów rozproszenia natężenie promieni roentgena, ich długość fali. Chociaż wiązka padająca składa się z jednej fali λ rozproszone promienie roentgena mają maksimum natężenia przy dwóch długościach fali. W zjawisku Camptona fotony nie są absorbowane, lecz rozpraszane nie sprężyście ze zmianą energii E=hv` dla E=hc. Cząstka jako fala - fale materii. W 1924 r. francuski uczony Louis de Broglie na podstawie teoretycznych rozumowań doszedł do następujących wniosków: Pod wieloma względami przyroda jest zadziwiająco symetryczna, Nasz dostrzegalny Wszechświat składa się wyłącznie ze światła I materii. Sugestia de Broglie`a nie zwróciłaby większej uwagi, gdyby nie przewidział on długości tzw. fal materii. Założył on, że długość ta jest określona tym samym związkiem, który stosuje się dla światła , który wiąże długość fali świetlnej z pędem fotonów. W równaniu tym, jak również w równaniu E=hy wyraźnie ujawnia się dwoista natura światła. Każde z tych równań zawiera w swojej strukturze zarówno pojęcie falowe (v,λ) jak I cząstkowe (E I p.). De Broglie przewidział, że długość fali materii jest dana również równaniem , gdzie p oznacza teraz pęd cząstki elementarnej. W 1926 r. wykonano doświadczenie, w którym skierowano wiązkę elektronów o odpowiedniej energii na kryształ. Atomy kryształu służą jako ugrupowanie celów dyfrakcyjnych dla elektronów. Powinniśmy więc poszukać silnych maksimów dyfrakcyjnych w pewnych charakterystycznych kierunkach.
Doświadczenie to pozwoliło sformułować argument, że w pewnych okolicznościach elektrony wykonują naturę falową (również inne cząstki, naładowane I nienaładowane). Zarówno dla materii jak I dla światła musimy przyjąć dwoisty charakter. Materia w pewnych okolicznościach zachowuje się podobnie jak cząstka, w innych podobnie jak fala. Kreacja par cząstka - antycząstka . Dualny charakter fali elektromagnetycznej . Kreacja par - tworzenie par , jeden ze sposobów oddziaływania promieniowania ? z materią . W procesie tym kwant ? oddziałuje z polem elektrostatycznym jądra atomowego lub elektronów w atomie , zmieniając się na parę elektron - pozyton . Energia progowa γ kwantu γ potrzebna do kreacji par elektron - pozyton w polu elektrostatycznym jΉdra wynosi ; gdzie - masa spoczynkowa elektronu ; c - prędkość światła w próżni , a w polu elektrostatycznym elektronu wynosi . Anihilacja par cząstka - antycząstka (atomów elementarnych) . Jest to zjawisko znikania pary cząstka - antycząstka , w wyniku ich wzajemnego zderzenia . Produktem takiego oddziaływania mogą być kwanty γ promieniowania elektromagnetycznego , lub inne czΉstki elementarne . W najczęściej obserwowanej anihilacji elektron - pozyton , w zależności od ustawienia spinów obu cząstek jest możliwa emisja trzech , dwóch lub jednego fotonu , przy czym ostatni przypadek , ze względu na zachowanie pędu może zachodzić tylko podczas obecności trzeciego ciała . Przy wyższych energiach a także w zderzeniach cząstek ciężkich ( np. proton - antyproton ) oprócz kwantów ? , obserwuje się zazwyczaj pewną liczbę hadronów ( cząstek biorących udział w oddziaływaniach silnych ). Zjawisko anihilacji par można obserwować podczas przechodzenia pozytonów przez materię . Pozyton najpierw traci większą część swojej energii wewnętrznej w zderzeniach z atomami . Spowolnione pozytony szybują przez materię i ewentualnie mogą być wyłapane przez elektrony w atomach . Proces anihilacji zapisujemy wzorem γ - foton ( kwant ) .	Fale materii - konsekwencje - zasady nieoznaczoności . Fale materii ( patrz pkt. cząstka jako fala - fale materii ) Zasada nieoznaczoności - fakt ,że nie możemy opisać ruchu elektronów w sposób klasyczny znajduje wyraz w zasadzie nieoznaczoności podanej przez Wernera HEISENBERGA w 1927 r. Szczególnym przypadkiem tej zasady jest równanie ΔΔy≅h. W równaniu tym Δ oznacza niepewność naszej znajomości pionowej składowej pędu , a ?y oznacza niepewność pionowej składowej położenia . Równanie to głosi , że iloczyn tych niepewności jest wielkością stałą tzn. Nie możemy mierzyć jednocześnie i y z nieoznaczoną dokładnością . Ogólna zasada nieoznaczoności w zastosowaniu do pomiarów położenia i pędu ma postać : . Zasada nieoznaczoności wyjaśnia nam , jak jest możliwe to , że zarówno światło jak i materia mają dwoistą , falową - cząstkową naturę . Pochodzi to stąd , że te dwa aspekty nie mogą nigdy równocześnie ujawnić się w tych samych okolicznościach i warunkach . Pierwszym , który wykazał , że pojęcia fali i cząsteczki uzupełniają się był Niels BOHR . Kwantyzacja Schrodingera - zasada falowej mechaniki kwantowej . Mechanika kwantowa jest to dział mechaniki zajmujący się ruchem mikrocząstek . Stanowi podstawę fizyki cząstek elementarnych , jądra atomowego , atomu i cząstki , fizyki ciała stałego . Opiera się na kilku postulatach , zrywających z tradycyjnym sposobem opisu ruchu , opartych na pełnych deterministyczne . Przekonanie , że stany stacjonarne w atomach odpowiadają stojącym falom metali , powzięte zostało przez Erwina SCHRODINGERA i wykorzystane jako podstawa mechaniki kwantowej. Postulaty: W mechanice gazowej pełna informacja o stanie cząstki jest zawarta w funkcji falowej ? , będącej funkcją położenia cząstki oraz czasu . Kwant modułu funkcji falowej określa gęstość prawdopodobieństwa znalezienia cząstki w określonej chwili i miejscu . Funkcję falową nierelatywistycznej mechaniki kwantowej wyznaczamy rozwiązując równanie	Schrodingera .. Mechanika kwantowa uwzględnia specyfikę aktu pomiaru , a zwłaszcza ograniczoną dokładność . Jednym z najważniejszych twierdzeń jest zasada nie rozróżnialności jednakowych cząstek , która głosi , że przedstawienie cząstek tego samego rodzaju nie zmienia gęstości prawdopodobieństwa dla stanu kwantowego układu . Każdej mierzalnej wielkości fizycznej przypisuje się w mechanice kwantowej pewien operator . Mierząc określoną wielkość fizyczną otrzymuje się tylko taki wartości , które pokrywają się z wartościami własnymi operatora odpowiadającego tej wielkości . Mechanika kwantowa wyjaśnia wiele faktów doświadczalnych odkrytych wcześniej i niewytłumaczalnych na podstawie fizyki klasycznej oraz przewiduje wiele nowych zjawisk . Kwantyzacja Plancka , Einsteina , Bohra określonych zagadnień . 1) Prawo Planck'a dla promieniowania ciała doskonale czarnego : Ciało doskonale czarne - ciało całkowicie pochłaniające padające na nie promieniowanie , niezależnie od jego składu widmowego i temperatury . Współczynnik absorpcji ( pochłaniania ) wynosi 1. Prawo Planck'a - zostało przez niego wyprowadzone na podstawie dwóch założeń ( oscylator nie może mieć dowolnej energii , lecz tylko osiągnąć energię E=nhv oraz oscylatory nie wypromieniowują energii w sposób ciągły , lecz skokami , czyli kwantami . Właśnie ma podstawie tych założeń Planck na drodze teoretycznej otrzymał wyrażenia na własności stałych , które do tej pory otrzymywano doświadczalnie : : . Falowa teoria Einsteina - Einsteinowi udało się wyjaśnić efekt fotoelektryczny dzięki całkiem nowemu założeniu , mianowicie , że energia wiązki świetlnej rozchodzi się w przestrzeni skończonych porcji energii zwanych fotonami . Energia pojedynczego fotonu wynosi E=hv . Hipoteza Einsteina sugeruje , że światło rozchodzące się w przestrzeni zachowuje się nie jak fala , lecz jak cząstka . Jeżeli teorie tę zastosujemy do efektu fotoelektrycznego dostaniemy : . Model Bohra atomu wodoru - wyjaśnienie obserwowanych zjawisk nigdzie nie znajdą lepszych ilustracji niż w rozwoju modeli atomu . Kluczowym faktem prowadzącym ostatecznie do koncepcji falowo	- mechanicznej atomu , było liniowe widmo wodoru . Badanie widma wodoru doprowadziło Niela Bohra do sformułowania postulatu , że kołowe orbity elektronów są kwantowane tj. że ich moment pędu może mieć wartość równą wyłącznie którejś z całkowitej wielokrotności pewnej podstawowej wartości . Pomocną przy tworzeniu tej teorii była zasada odpowiedzialności , mówiąca , że fizyka kwantowa przechodzi w fizykę klasyczną przy dużych wielkościach kwantowych . Skręcenie płaszczyzny polaryzacji . Płaszczyzna polaryzacji - jest to płaszczyzna , w której leży wektor H ,a kierunek rozchodzenia się fali jest prostopadły do płaszczyzny drgań . Podczas przejścia przez kryształ , światło ulega polaryzacji i w zależności od płaszczyzny drgań fali świetlnej inaczej przechodzi przez kryształ . Np. w krysztale szparu irlandzkiego , po wejściu do płytki światło rozdziela się na dwa promienie . Jeden z nich przechodzi przez kryształ bez zmiany kierunku ( zwyczajny ) , a drugi ulega odchyleniu ( nadzwyczajny ) . Jednak po wyjściu z kryształu oba promienie są równoległe . Aktywność optyczna - inaczej własność skręcenia o pewien kąt płaszczyzny polaryzacji światła przechodzącego przez niektóre ośrodki . Naturalna aktywność optyczna jest związana z asymetrią cząstek , a w krysztale - z rozmieszczeniem atomów w sieci krystalicznej . Zjawisko to wykorzystuje się w przyrządach mierzących metodami optycznymi stężenie roztworów ( np. w polarymetrach ) .Miarą zdolności skręcającej do danego ciała jest stosunek kąta skręcenia płaszczyzny do grubości próbki ( w stopniach na centymetr ) . Polaryzacja - metody polaryzacji światła ( metody naturalne i wymuszone ) . Polaryzacja światła jest to uporządkowanie kierunków drgań wektorów E i H fali świetlnej . Kierunek drgań wektora pola elektrycznego E i magnetycznego H światła spolaryzowanego pozostaje niezmieniony w przestrzeni lub zmienia się według określonego prawa . Płaszczyzna utworzona z kierunku drgań wektora E i kierunku rozchodzenia się fali (prostopadła do kierunku drgań) nosi nazwę płaszczyzny polaryzacji. Najogólniejszym przypadkiem polaryzacji jest polaryzacja eliptyczna , a jej szczególnymi przypadkami są ; polaryzacja liniowa i kołowa . Światło naturalne
(nie spolaryzowane), np. światło słoneczne , można spolaryzować na kilka sposobów : Przepuszczając przez polaroid , Przepuszczając przez pryzmat polaryzujący , W wyniku odbicia pod kątem Brewstera od jednej lub więcej płytek szklanych lub dialekurynnych Praca i moc prądu zmiennego. Praca i moc prądu zmiennego. Praca wykonywana przez prąd stały, którego natężenie jest skuteczną wartością prądu zmiennego wyraża się wzorem: W = UIt, lecz prąd zmienny wciąż zmienia swoje natężenie, zatem jego pracę w czasie da wzór: praca czynna - jest całką lub połową napięcia, natężenia i okresu. , ale ponieważ I i U podaje się jako wartości skuteczne, więc: praca bierna - , razem: Praca całkowita:

6

---