0117

118

II. Funkcje jednej zmiennej

Udowodniona własność nieskończenie małych prowadzi do jej wykorzystania przy badaniu wyrażeń nieoznaczonych postaci 0/0, tj. przy badaniu granicy ilorazu dwóch nieskończenie małych 0/a. Każda z tych nieskończenie małych może być przy tym zastąpiona, bez wpływu na wielkość granicy, dowolną inną równoważną jej nieskończenie małą.

Rzeczywiście, jeżeli a~x i 0~0, tj.

to iloraz

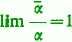
oraz lim—=1,

P

L=Ł.Ł.±

a 0 a a

różniący się od ilorazu /?/<* czynnikami dążącymi do jedności, ma granicę równocześnie z nim (tę samą). Jeżeli udaje się wybrać a i 0 możliwie prostej postaci, to możemy znacznie uprościć zagadnienie; np.

*\/l "b—1 ..    ) 1

hm--—lim-=— •

*-.o sin 2*    ,-0 2x 4

Z dowodu wynika od razu także, że dwie nieskończenie małe równoważne trzeciej, są równoważne sobie.

63. Wydzielenie części głównej. Jeżeli wybrano podstawową nieskończenie małą a, to najprostszymi nieskończenie małymi są oczywiście wielkości postaci c ■ tx^k, gdzie c jest stałym współczynnikiem, a k>0. Niech nieskończenie mała fi będzie k-tego rzędu względem

«,.i.

lim -j=c, a

gdzie c jest liczbą skończoną i różną od zera. Wówczas

lim — = 1 , ca

a nieskończenie małe fi i ca* okazują się równoważne: fi~cix^k.

Ta najprostsza nieskończenie mała ca*, równoważna danej nieskończenie małej fi, nazywa się jej częścią główną.

Posługując się otrzymanymi powyżej rezultatami, poza już wskazanymi prostymi przykładami, łatwo wydzielić części główne wyrażeń

1— cosjc~ł;c² ,    tg* —sin*~i*³ .

Tutaj *->0, i a = x okazuje się najprostszą nieskończenie małą.

Jeżeli natomiast x-»+oo, i za podstawową przyjęto nieskończenie małą a = l/*, to mamy także

* + l 4-‘s/x — 1—2.\jx~--j —

4 \x

Wszystkie te wyniki prowadzą do wzorów przybliżonych.

Niech /ł~ca*, tj. 0=ca*+y, gdzie y=o(a*). Można wyobrazić sobie, że z nieskończenie małej y znowu wydzielono część główną: y = c'a*’+<5, gdzie k’>k, a S=o(a*'), itd.

Jeżeli np. przyjąć (przy jc->0):

7l+i-l=— x+y,

m