0153

154

II. Funkcje jednej zmiennej

mają tę własność, to dowolną z nich). Ten przedział znowu podzielmy na połowy, i oznaczmy przez <a₂, b₂} tę z jego połówek, która nie ma pokrycia skończonego, itd.

Kontynuując ten proces otrzymujemy nieskończony ciąg przedziałów zstępujących <a„, b„} (n = l, 2, 3, ...), z których każdy jest połową poprzedniego. Przedziały te są tak dobrane, że żaden z nich nie ma skończonego pokrycia. Na mocy lematu o przedziałach zstępujących [38] istnieje wspólny tym przedziałom punkt c, do którego dążą punkty a_n i b„.

Punkt c, jako jeden z punktów przedziału (a, by, leży w jednym z przedziałów a, np. a o=(^a> fi), czyli jest a < c < fi. Ponieważ punkty a„ i b_n dążą do c, to poczynając od pewnego n zawierają się one w przedziale er₀ (26,1°), tak że wyznaczony przez nie przedział (a„, b„y okazuje się pokryty tylko jednym przedziałem a₀, wbrew wyborowi przedziałów <a„, b„y. Otrzymaliśmy sprzeczność, co dowodzi, że lemat jest prawdziwy.

Przytoczymy jeszcze jeden dowód, oparty na innym pomyśle, pochodzący od H. Le-besgue’a.

Dowód II. Rozważmy punkty x* przedziału <a, by o tej własności, że przedział <a, x*y jest pokryty skończoną ilością przedziałów a. Takie punkty x* istnieją; jeżeli np. punkt a leży w jednym z przedziałów a, to i wszystkie najbliższe mu punkty leżą w tym przedziale, a więc są punktami typu x*.

Naszym celem jest ustalenie faktu, że punkt b jest również punktem typu x*.

Ponieważ wszystkie x*^b, istnieje [11] także

sup {x*} = c^b.

Jak każdy punkt przedziału (a, by, punkt c należy do pewnego <r₀=(a, fi), a<c<fi. W takim razie z własności kresu górnego znajdziemy takie jcJ, że a<xj<c. Przedział (a, x*y pokryty jest skończoną ilością przedziałów a (z samej definicji punktów typu x*); jeżeli do tych przedziałów dołączyć jeszcze jeden przedział a₀, to pokryjemy już cały przedział <a, c>, tak że c jest typu x*.

Jednocześnie jest jasne, że c nie może być mniejsze od b, bo inaczej pomiędzy c i fi znaleźlibyśmy jeszcze punkty typu x *, wbrew definicj liczby c jako kresu górnego punktów typu x*. Tak więc musi być b — c; oznacza to, że b jest typu x*, tj. że przedział <a, ń) pokryty jest skończoną ilością przedziałów a, co należało okazać.

Zauważmy, że dla słuszności lematu w równej mierze ważne jest założenie o domknię-tości podstawowego przedziału <a, by, jak i założenie, że przedziały a tworzące układ 27 są otwarte. Na przykład układ przedziałów otwartych

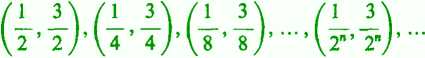
pokrywa przedział (0, 1>, ale z tego układu nie można wydzielić skończonego pokrycia tego przedziału. Podobnie układ przedziałów domkniętych

<1,2>

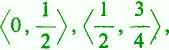
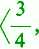
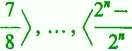
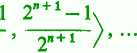
pokrywa przedział <0, 2>, ale i tutaj wydzielenie skończonego pokrycia nie jest możliwe.