030 031

50

Działania zdefiniowane w dwuelementowej algebrze Boole'a, zaróvC^ podstawowe Jak i złożone, nazywamy funkcjami logicznymi. Wymienione tożsamości (T) t (2^ pozwalają upraszczać wyrażenia opisujące wieloargumento-we funkcje logiczne, ułatwiając Ich analizę.

Przykład 1.19

Uprościć funkcję logiczną daną wyrażeniem

f(x,y,z) = xz +■ xyz + yz + xyz.

Korzystając z tożsamości o numerach wypisanych między znakami równości, realizujemy następujący ciąg przekształceń

f(*,y,z) =	©	= xz • xyz • yz + xyz =
©	©	= (x + z)(x + y + z)(y + ź) + xyz =
	®	= [x(x+y+ź) + z^r+y+z}] {j+z)+ xyz =
	©	= [_ xx+xy+źT (x+x+y+ź") ] (y+z) + xyż =
©©	(D	= [^ly’ + iT(1+y+z)](y+z’) + xyz =
®	©	= (xy+z)(y+z) + xy¥ =
©	©	= z+xyy + xy7 = ©(© © (?) = z+zyź'
0	©	= z

Inną, oprócz wyrażeń, formą zapisu funkcji logicznej Jest tablica,w której) wszystkim możliwym wartościom argumentów przyporządkowuje się odpowiednie wartości funkcji.

Przykład 1.20

Funkcję f = xyzw + xzw + xw + y przedstawić w tablicy.

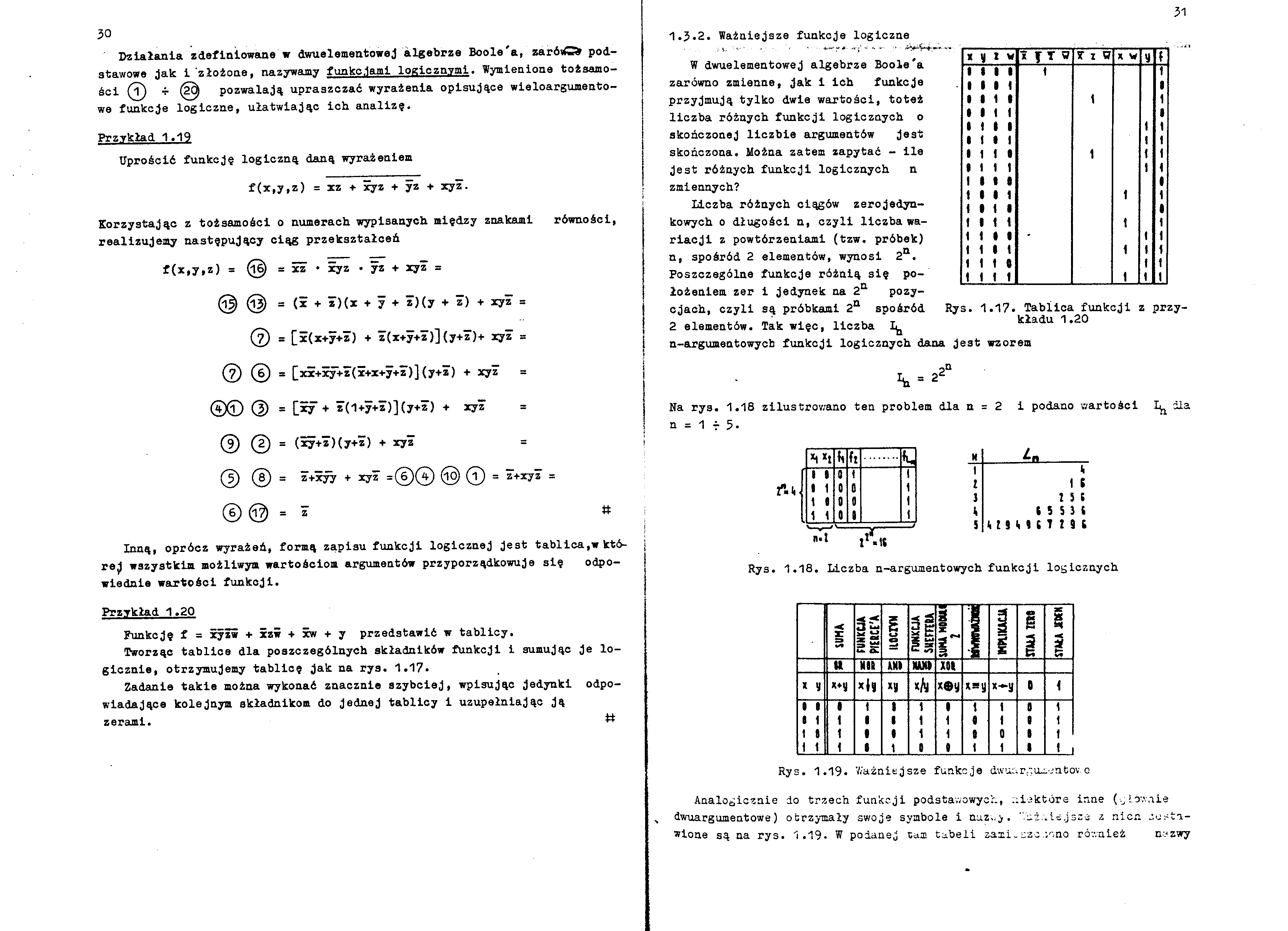
Tworząc tablice dla poszczególnych składników funkcji i sumując je logicznie, otrzymujemy tablicę Jak na rys. 1.17.

Zadanie takie można wykonać znacznie szybciej, wpisując jedynki odpowiadające kolejnym składnikom do Jednej tablicy i uzupełniając ją zerami.

1.3.2. Ważniejsze funkcje logiczne

1 | 1 V	tfT5	li!	X w	y	f
1 1 1 1	1				i
1 1 1 1					i
1111		1			1
1 1 1 1					a
1 1 1 1				i	i
1 t I 1				i	i
1111		1		i	i
1111				i	i
1 1 1 1					i
fili			1		i
1 ł 1 •					i
1111			1		i
1 1 • •	'			i	i
1111			1	i	i
1 1 1 {				i	i
1111		1		i	i

W dwuelementowej algebrze Boole'a zarówno zmienne, jak i Ich funkcje przyjmują tylko dwie wartości, toteż liczba różnych funkcji logicznych o skończonej liczbie argumentów jest skończona. Można zatem zapytać - ile jest różnych funkcji logicznych n zmiennych?

Liczba różnych ciągów zerojedynkowych o długości n, czyli liczba wariacji z powtórzeniami (tzw. próbek) n, spośród 2 elementów, wynosi 2ⁿ.

Poszczególne funkcje różnią się położeniem zer i jedynek na 2^a pozycjach, czyli są próbkami 2^a spośród Rys. 1.17. Tablica funkcji z przy-2 elementów. Tak więc, liczba 1^    kładu 1.20

n-argumentowych funkcji logicznych dana jest wzorem

Na rys. 1.18 zilustrowano ten problem dla n = 2 i podano wartości 1^ dla n = 1 r 5-

*1*1	(i	fi		K
i «	0	1		i
t i	0	0		1
i a	0	0		i
1 i	0	1		i

N	U
i	k
i	1 (
i	I 5 5
k	( 5 5 3 (
s	wsiiuim

Rys. 1.18. Liczba n-argumentowych funkcji logicznych

	■< X. ta	32 5 ***' i*. a	U 1 S ;	3 & sE	1 r	j	i £	g 1	ae § -< i
■■	anunacmisi
* y	**y	*ł!	*y	*/y	*©y	*=y	*-y	0	i
a a	a	i	i	i	a	1	i	a	1
a i	i	a	a	i	i	a	i	a	1
i a	i	a	a	1	i	a	0	i	i
i t	i	a	i	0	a	i	i	a	Lu

Rys. 1.19. Ważniejsze funkcje dwunrgumoatoy.o

na zwy

Analogicznie do trzech funkcji podstawowych, niektóre inne (glównie dwuargumentowe) otrzymały swoje symbole i naz..y. luźniejsze z aica zostawione są na rys. 1.19. W podanej tam tabeli zaii.szc.;ono również