Image051

V

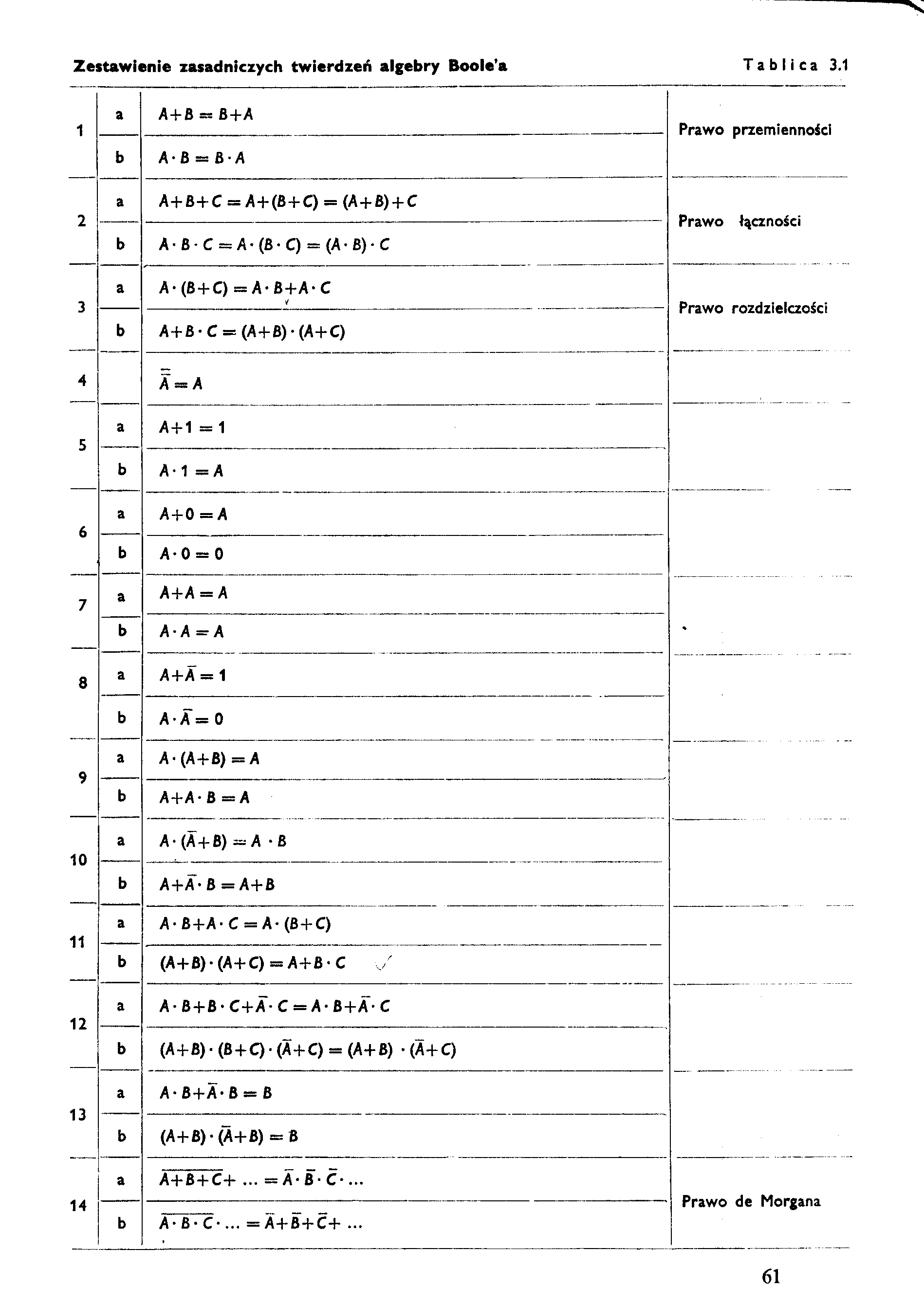
Zestawienie zasadniczych twierdzeń algebry Boole’a    Tablica 3.1

1	a	A + B«B+A	Prawo przemienności
	b	A* fi — fi - A
*5	a	A+B+C == A+(6+C) » (A + B) + C	Prawo łączności
	b	A' 6 * C = A • (6 • C) — (A • fi) * C
3	a	A* (B+C) = A* B+A* C *	Prawo rozdzielczości
	b	A+B • C = (A+B) • (A+C)
4		A = A
5	a	A + 1 = 1
	b	A* 1 = A
6	a	A-J-O = A
	b	A- 0 = 0
7	a	A+A = A
	b	A* A — A	*
8	a	A+A =s 1
	b	A-A — 0
9	a	A* (A+B) = A
	b	a+a* B = A
10	a	A* (A + B) = A *B
	b	A+A* B = A+B
11	a	A • B+A ■ C — A - (B + C)
	b	(A+B) - (A+C) = A+B • C /
12	a	A*B + B*C+A*C^A*B+A*C
	b	(A+B)* (B+C)• (A+C) = (A+B) *(A+C)
13	a	A* B+A* B = 6
	b	(A+B) • (A-^ B) = B
14	a	A+B + C+ ... = A* B • C*...	Prawo de Morgana
	b	A * B • C*... = A+B + C+ ...

61