0405

406

VI. Wyznaczniki funkcyjne i ich zastosowania

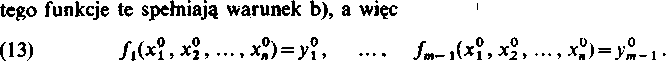
Wynika stąd, że m-ta funkcja (12a) jest także ciągła i ma ciągłe pochodne i wreszcie wobec 03) i (9):

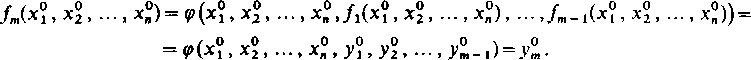
Twierdzenie jest udowodnione.

Uwaga. Zwracamy uwagę czytelnika na lokalny charakter wszystkich twierdzeń o istnieniu funkcji uwikłanych, mówi się w nich zawsze tylko o pewnym otoczeniu rozpatrywanego punktu. Lecz i takie twierdzenia są użyteczne, na przykład — jak się czytelnik przekona w rozdziale VII — przy badaniu własności jakiegoś tworu geometrycznego w danym jego punkcie zupełnie wystarcza ograniczenie się do bezpośredniego otoczenia tego punktu.

209. Obliczanie pochodnych funkcji uwikłanych. Rozumowania, za pomocą których udowodniliśmy twierdzenie o istnieniu funkcji uwikłanych nie dawały żadnego ogólnego wyobrażenia o tym, jak obliczać pochodne rzędu pierwszego funkcji uwikłanej. O pochodnych wyższych rzędów w ogóle nie było mowy. Zatrzymamy się teraz specjalnie na tych ważnych zagadnieniach.

Zaczniemy od najprostszego przypadku, gdy dane jest jedno równanie (1). Będziemy zakładali, że w otoczeniu rozpatrywanego punktu spełnione są wszystkie założenia twierdzenia II, szczególnie ważną rolę będzie odgrywał w dalszym ciągu warunek F^/0.

Pokażemy prosty sposób obliczania pochodnej /, jeżeli z góry wiadomo, że pochodna ta istnieje. Wiemy już, że jeżeli wstawimy funkcję uwikłaną y=f(x) w równanie (1), to otrzymamy tożsamość (patrz (2), ustęp 205). Zatem jeżeli przez y rozumieć tę właśnie funkcję x, to funkcja F(x, y) występująca z lewej strony równania (1) staje się funkcją złożoną zmiennej x, równą tożsamościowe zeru. Jej pochodna względem x jest wówczas także równa zeru. Jeśli zróżniczkujemy tę funkcję według reguły z ustępu 181, otrzymamy

(14)

Stąd

F'_x(x,y) + F'_y(x,y)y' = 0C).

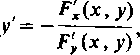
(15)

bo Fy# 0. Otrzymaliśmy znany nam już wzór (3) z ustępu 206.

Możemy teraz pójść dalej. Jeżeli funkcja F(x, y) ma ciągłe pochodne drugiego rzędu, to wyrażenie stojące z prawej strony wzoru (15) można zróżniczkować względem x i tym samym istnieje pochodna funkcji y', tzn. druga pochodna y" funkcji uwikłanej y. Wyko- ¹

1

Tego samego typu rozumowanie przeprowadziliśmy właściwie już wyżej. Patrz notka na str. 405.