1

Ćwiczenie 40

Wyznaczanie modułu sprężystości przy pomocy wahadła torsyjnego

40.1. Wstęp teoretyczny

Jeśli jeden z końców długiego jednorodnego pręta sztywno zamocować, a do drugiego przyłożyć skręcający moment sił M, to koniec ten przekręci się o kąt <p, zgodnie z zależnością:

M = D-<p    (40.1)

Dla danego pręta stała wielkość D nosi nazwę modułu skręcenia lub momentu kierującego. Liniowa zależność pomiędzy M i (p wyrażona wzorem (40.1) zachodzi tylko dla niewielkich wartości M. W ogólnym przypadku zależność ta może być nieliniowa lub nawet niejednoznaczna. Wielkość D nie charakteryzuje jednoznacznie właściwości materiału podczas skręcenia, dlatego wprowadza się inną wielkość nazwaną modułem sprężystości G.

Wprowadzimy teraz zależność wiążącą moduł sprężystości G oraz moduł skręcenia D. Po odchyleniu dała o kąt a od położenia równowagi wytwarza się nowy stan równowagi, w którym moment M równoważy moment siły zewnętrznej M_z. Po uwolnieniu ciała powstają drgania pod wpływem momentu siły M?

M_t=-D‘<x    (40.2)

zawsze zwracającego ciało do położenia równowagi. Równanie ruchu ma postać analogiczną do równania ruchu dla wahadła grawitacyjnego:

jSg-=-Da    (40.3)

dr

Okres drgań dla tego ruchu wyraża się wzorem:

T —

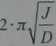
(40.4)

gdzie / jest momentem bezwładności drgającej bryły względem zadanej osi obrotu.