3582468732

1. Temat:

Wyznaczanie przyspieszenia ziemskiego przy pomocy wahadła matematycznego.

2. Wprowadzenie teoretyczne:

Wahadłem matematycznym nazywamy punkt materialny zawieszony na nierozciągliwej i nieważkiej nici. Jest to idealizacja wahadła fizycznego.

Ważną cechą wahadła matematycznego jak i fizycznego jest niezależność okresu drgań od maksymalnego wychylenia dla niewielkich wychyleń wahadła.

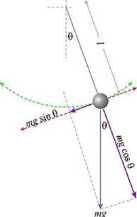
Analiza ruchu wahadła:

W wahadle matematycznym poruszające się ciało jest punktem materialnym, zawieszonym na nieważkiej, nierozciągliwej nici o długości /. Na ciało to działa stała siła grawitacji. Gdy wahadło odchylone jest z położenia równowagi, składowa siły grawitacji wzdłuż nici jest równoważona przez nić, a składowa prostopadła do nici działająca w kierunku punktu równowagi nadaje ciału przyspieszenie. Ruch ciała ograniczony nicią jest ruchem po okręgu. Z definicji przyspieszenia kątowego oraz z II zasady dynamiki dla ruchu punktu materialnego po okręgu, dla kątów wyrażonych w mierze łukowej kąta, wynikają zależności:

_d?0

dt²

,    „    ,2 <P0

di²

—mglsm 9 = ml ■

Przybliżenie małej amplitudy

Dla małych wychyleń, 0 jest bliskie zera, wówczas funkcję sinus można przybliżyć jej argumentem co prowadzi do równania: j2q _

dC ^hT^{0 = O}

Powyższe równanie jest równaniem ruchu drgającego harmonicznego, którego ogólna postać jest dana wzorem:    j2 q

dt²

+ v²$ = 0

2tt

gdzie >.} = _ jest częstością kołową drgań a T - okresem.

T

Wynika stąd, że okres drgań wynosi: T = 2tt

Takie drgania wahadła matematycznego (bez działania sił zewnętrznych) nazywamy drganiami własnymi wahadła.