3

318

Ćwiczenia laboratoryjne z fizyki

Powierzchnia ils przekroju pierścienia ograniczonego obwodem o promieniu r i r‘ + dr wynosi 2nr'dr'. Wartość siły styczne; działające; na taki pierścień wyraża się wzorem:

dF,=ds-T = 2irr'-dr‘-G~^a    (40.13)

a moment te; siły wyrażeniem:

dM = dF,

(r'f c

■r =2Jt-a-G-—-—dr

(40.14)

Całkując wyrażenie (40. i 4) w granicach od zera do r, otrzymuje się wartość momentu siły działającej na powierzchnię przekroju poprzecznego drutu:

M = f2jr-a-G-~--dr‘ ⁼^~JTf~'^a    (40.15)

Drugą zasadę Newtona (40.2) i (40.3) można dla tego przypadku zapisać w postaci:

	1 , d^1a n-G-r* " ^J e,‘ - 27	(40.16)
stąd:	i Bilion/	(40.17)

Mierząc okres T, można wyznaczyć wartość modułu sprężystości G ze wzoru:

|    ...

G= g| p    (40.18)

Zależność między modułem skręcenia a modułem sprężystości wynika z zależności (40.17) i jest następująca:

„ nGr*

^D=-JJ~    (40.19)

40.2. Opis układu pomiarowego

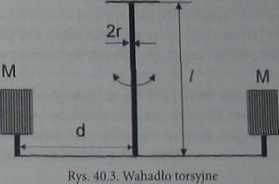
Obiektem badań jest pręt o długości / i średnicy 2r, którego górny koniec jest sztywno zamocowany, drugi dolny jest poddawany działaniu sił skręcających (rys. 40.3).

W dolnej części pręta zamocowane jest ramię o długości 2d, na którego końcach znajdują się dwa stanowiska do zamocowania walców wykonanych z różnych materiałów i posiadających różne masy. Odchylony w płaszczyźnie poziomej układ

Ćwiczenie 40

319

wykonuje drgania torsyjne. Taki układ jesl jednym z przykładów wahadła fizycznego i nosi nazwę wahadła torsyjnego. jak dla każdego wahadła fizycznego, jego okres zależy od jego momentu bezwładności (wzór (40.4)).

Ze wzoru (40.4) wynika, że dla wyznaczenia modułu skręcenia, a następnie modułu sprężystości wystarczy zmierzyć okres drgań wahadła i wyznaczyć jego moment bezwładności. Jednak bezpośrednie wyznaczenie momentu bezwładności jest trudne. Trudność tę można ominąć w następujący sposób: zmierzyć najpierw okres drgań T₀ wahadła nieobciążonego o pewnym nieznanym momencie bezwładności a następnie zmierzyć okres T drgań wahadła obciążonego dodatkowym ciałem o kształcie pozwalającym analitycznie obliczyć jego moment bezwładności /. Zapisując wzór (40.4) dla obydwu wymienionych przypadków, otrzymuje się:

Proste przekształcenia pozwalają wyeliminować z tych dwóch równań wielkość l₀ i otrzymać wyrażenie dla modułu skręcenia D:

Bp#p||r    (40.20)

Po podstawieniu wyrażenia (40.20) do zależności (40.19) otrzymuje się wyrażenie dla modułu sprężystości:

(40.21)

mm

r⁴ (T²-r₀^})

W przypadku, gdy na konstrukcję wahadła nałożone są symetrycznie dwa walce o jednakowej masie m, to przy założeniu, że ramię wahadła d jest znacznie większe niż wymiary walców, zmiana momentu bezwładności jesl równa:

(40.22)

J = 2-m-d²