706

706 Mierzenie wyników inwestycyjnych

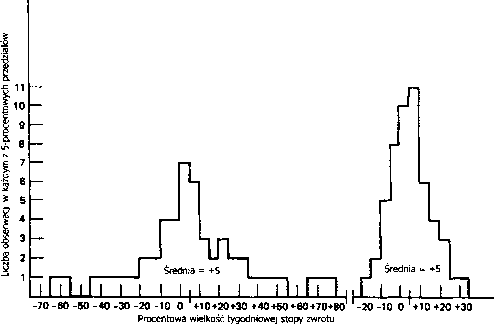
Diagram 21.2

Porównanie wyników dwóch menedżerów, którzy osiągają tę samą stopę zwrotu przy różnych odchyleniach standardowych.

W praktycznym zastosowaniu współczynnika Sharpe'a N jest równe liczbie interwałów czasowych. Jeśli na przykład dla okresu trzyletniego obserwuje się wyniki miesięczne, N będzie równe 36.

Przy obliczaniu odchylenia standardowego trzeba zawsze wybrać pewien interwał czasowy, który dzielić będzie badany okres (na przykład tydzień lub miesiąc). Jeśli procentowa stopa zwrotu zostanie rozbita na przykład na wielkości tygodniowe, odchylenie standardowe będzie wysokie wtedy, gdy stopy zwrotu w poszczególnych tygodniach będą się bardzo różnić od średniej dla całego okresu; będzie ono małe, gdy wielkości tygodniowych stóp zwrotu będą się skupiać w pobliżu średniej. Diagram 21.2 przedstawia dwa zbiory danych, dla których stopa zwrotu z całego okresu jest taka sama, natomiast ich odchylenia standardowe są wyraźnie różne.

Podstawowym założeniem współczynnika Sharpe'a jest przyjęcie odchylenia standardowego jako miary ryzyka. Oznacza to, że im bardziej rozrzucone są wielości poszczególnych stóp zwrotu, tym większe ryzyko inwestycji. Odchylenie standardowe odzwierciedla niepewność co do stopy zwrotu. Powinno być intuicyjnie zrozumiałe, że jeśli odchylenie standardowe jest niewielkie, można się spodziewać, że faktyczna stopa zwrotu będzie bliska oczekiwanej (przy założeniu, że oczekiwana stopa zwrotu jest dobrą wskazówką co do jej wielkości faktycznej). Z drugiej strony, jeśli odchylenie standardowe jest duże, należy uznać, że istnieje znaczne