DSC07298

18

Liczby zespolone

c) Mamy

> v'5|s-(l-»)l^⁴ <=> 1= - (^l — *)l & 2\/2.

Smk»nv zbiór składa się z punktów z położonych w odległości nie mniejszej niż r = 2^ od punktu -₃ = 1 - i. Jest to zatem zewnętrze kola o środku w punkcie so = 1 - ii promieniu r = 2V% Okrąg o promieniu r = 2^2 należy do tego zbioru (zobacz rysunek).

Im *

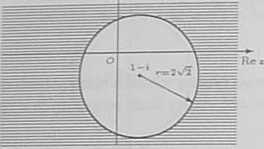
d) Dla z = 2£ mamy

|“] $ 1 <=>|c + 3|jlMi2i|-Z=*|z-(-3)| $ |z-2i|,

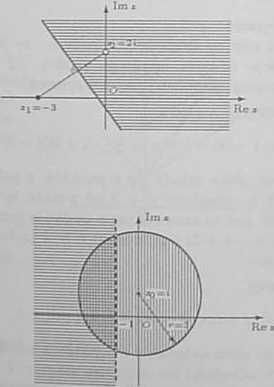
Szukany zbiór składa się z punktów z. których odległość od punktu :i = -3 jest nie mniejsza niż odległość od punktu z? = 2i. Jest to zatem półplasz-czyzna ograniczona symetralna odcinka o końcach z_It rj, bez punktu sj = 2ś. Symetralna ta należy do szukanego zbioru (zobacz rysunek).

e) Poszukiwany zbiór jest wspólną częścią zbiorów określonych przez warunki:

Be(z+l)<0, |i — jj § 3.

Pierwszy warunek określa lewą pół-płamezyznę otwarta ograniczoną pro-«ą i + 1 = 0. Drap warunek okre-fla kolo domknięte o środku w punk-“ *o = « i promieniu r = 3. Wspólna część tych zbiorów przedstawiono na rysunku.

0 Mamy

~ +**| * |s - 2i\

l(z + 2i)-(*_2i)|_$ |*_2i|

I* + 2i| - |z - 2i| $ |z — 2f |

I* - 2tj = 0 albo |z - 2i| > 0 oraz |z + 2i| $ 1.

Przykłady

19

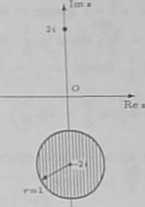
Warunek

|j - 2i| = O

wyznacza zbiór {2ił, a warunki

|j + 2i|$I oraz |z — 2£| > 0

określają kolo domknięte o środku w punkcie Jo = — 2i i promieniu r = 1. Sumę tych zbiorów przedstawiono na rysunku.

Postać trygonometryczna liczby zespolonej

• Przykład 1.9

Podane liczby zespolone zapisać w postaci trygonometrycznej: a) -t/5;    ’b)-6+6i;

d) ^3 + i;    e) sina — icosa; f) 1—ictga;

g*) 1 + cos a + i sin a.

Uwaga. W ćwiczeniach e), f*), g) kąt a spełnia nierówności 0 < a < —.

Rozwiązanie

Każdą liczbę zespoloną z można zapisać w postaci trygonometrycznej:

j = r (cos +«sin ifi),

gdzie r jest modułem, a f argumentem liczby z.

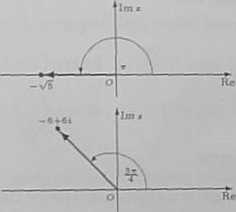
lm a

a)    Dla j = — y/5mamy r = v5 oraz <f — jt. Zatem

—y/h = V5 (cos - -I-1 sin w).

b)    Dla i = — 6 + 6i mamy r = 6y/2

3ir _ .

oraz ip ~ —. Zatem —0+6i = 6>/2 ^cos ^ + isin ■

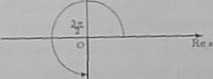
c)    Dla s = — 2i mamy r = 2 oraz __3ir „

•P ——. tatem

-2i = 2 ^cosIp + isin ■