DSC07302

26

Liczby zespolone

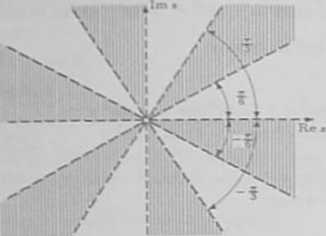
Poszukiwany zbiór składa się a sześciu otwartych obszarów kątowych (rysunek).

Przykład* 1.14

Wykorzystując wzór na sumę wyrazów zespolonego ciągu geometrycznego obliczyć j 1 + cos* + cos2x +... + coanx, gdzie n € N, z € R.

Rozwiązanie

Niech z = coai + i sin x. Wtedy z^k = cos kx + i sin fcr, zatem cos kx = Re z dla k = 0.1,2.....n. Stąd mamy

1 —

1+COSI+ — +cosnx = Re (1 + z +... + z") = Re—^ — - ■

= Re-

1 — cos (n + 1) x — tsin(n + l)x 1 — cos z — i sin x

= Re

_ . s (n + 1) x ... (n + l)x (n + 1)* 2 sin ■—--2i sin---cos-g-

2sin^a | -2isin|cos|

= Re

. (n + 1) x . (n + l)x . (n + I)x stn » ^aln " 2 ~^ICOS-2~—

: ł ^S,n2

X    x

«in- -IC06-

j (n+l)x	(_jn (n+l)x		(n+l)x\ / x
2 nr
Tx-"* *n 2	2	a O	^03 2 J l**" 2
. (»+l)x _
2 [.	. (n + l)x _f_	X	__ (n + l)x
■ * V «™ o '	MII ^ ■*“	2	^1 2 ^ro'

(n + l)g

nz

sin

i--"T-

Ostatai rachunek jot prawdziwy dla i / 1, to znaczy dla z / 2/.-ir, gdzie G Z. Dl® x =■ 2k» mamy 1 + coa2Jlnr + ... + ttmnTku = n + l.

Przykłady    ^

Postać wykładnicza liczby zespolonej

• Przykład 1.15

Stosując postać wykładniczą liczby zespolonej z rozwiązać podane równania:

.)(!)•-4 Mi    ......

Rozwiązanie

Zastępując symbolem e'* wyrażenie coa<p + i sin <p występujące w postaci trygonometrycznej liczby zespolonej z = r(cos ęj+isinip) otrzymamy postać wyklndaniczą tej liczby, tzn. wzór z = ref*. Przy rozwiązywaniu równań będziemy korzystać z tego, że dwie nie-zerowe liczby zespolone są sobie równe wtedy i tylko wtedy, gdy ich moduły są równe, a argumenty różnią się o wielokrotność 2ir, tzn. dla zi = r₁e‘^v’¹, z_a = rae***, ri,ra > 0, mamy

si = za <—» ri = ra oraz ęai = ipi + 2fcrr, k 6 Z. a) Liczba z = 0 spełnia równanie (s)* = 4 jz^a|. Niech teraz z = re**, gdzie r > 0, 0 $ ip < 2-. Wówczas z = re^-up oraz, ze wzoru de Moivre'a, (z)® = r*e^-®^,v>. Dalej |z^a| = r^a, a więc

(-)° ⁼ 4 |z*|

pOg-Olsj ₌ 4r3

= 4re

f r® = 4r^a —6<p = 0 + 2łnr, k

mm

ez

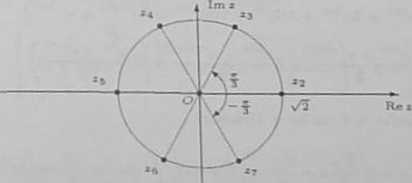
r = 0 lub r = >/2 V== y. / = 0,1,2,3,4,5.

Rozwiązaniami równania są zatem liczby

_St=0.za^t/2,za = ^ ₊ ^.-.

y/2 . >/6.

—5“ + -j"*. =s = —sa, za = ~-3* zt = -=4.

Są one przedstawione na rysunku poniżej.

b) Równoważnie możemy napisać, że |z|^a z = (-1)- (5)* dla : jSO. Niech z = re'*, gdzie r > 0, 0 $ <p < 2ir. Wówczas

|z|^a • z = (-1) - (=)» <=> r^a . (re**) = e" . (r^se-^,i'’)

r* == r*

= ir —    4- 2Anr, k 6 Z