img066

66

6. Metody aproksymacyjne

rodziny O. Po drugie, wygodnie jest dysponować rodziną funkcji ortogonalnych lub jeszcze lepiej ortonormalnych, to znaczy spełniających warunki

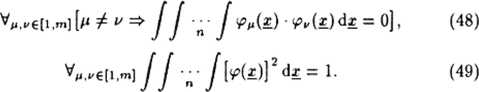
Ortonormalność funkji bazowych powoduje, że poszczególne wagi V* mogą być wyznaczane niezależnie, a błąd wyznaczenia jednej z nich nie wpływa na błędy wyznaczenia pozostałych. Powstaje jednak problem, jak znaleźć rodzinę ortonormalnych funkcji n zmiennych (argument x jest wektorem), gdyż dobrze znane są jedynie odpowiednie rodziny funkcji jednej zmiennej (na przykład rodziny funkcji trygonometrycznych, wykładniczych, wielomianów Czebyszewa itp.). Zanim podamy propozycje jednej z metod tworzenia rodziny funkcji 4>, musimy zastanowić się nad możliwością spełnienia warunku (46) i nad zapewnianiem zbieżności szeregu (47).

Niewiele wiedząc o charakterze funkcji przynależności C'(x), możemy jednak przypuszczać, że są to funkcje w miarę gładkie o małej dziwaczności (por. [5]). Pojęcie dziwaczności, ma charakter intuicyjny i nieformalny, ale można je sprecyzować na przykład w ten sposób, że funkcję będziemy uważać za tym bardziej dziwaczną, im więcej ma ekstremów' w pewnym ustalonym przedziale zmienności swoich argumentów. Przypuszczenie o małej dziwaczności funkcji przynależności C*(x) wynika z intuicyjnego przekonania o regularnym kształcie klas w przestrzeni X, gdyż dobre odseparowanie obszarów' należących do różnych klas pozwala na ich rozgraniczenie stosunkowo gładką hiperpowierzchnią w n-wymiarowej przestrzeni (por. rys. 6.1). Równanie hiperpowierzchni rozgraniczającej klasę /i od v ma oczywiście postać:

C»(x) - C^v(x) = 0.

(50)

Gładkość granic obszarów' w' przestrzeni A' determinuje więc małądziwacz-

ność funkcji C^ł(x) i na odwrót.

Jeśli teraz rodzinę funkcji 4> wybierzemy w ten sposób, aby ze wzrostem numeru porządkowego v harmonik v?t/(x) rosła ich dziwaczność (własność taką mają liczne rodziny funkcji jednej zmiennej, na przykład wielomiany Czebyszewa), to wówczas warunek (47) będzie prostą konsekwencją oczywistego faktu, że do budowy funkcji w ograniczonym stopniu dziwacznej nie trzeba używać wysoce dziwacznych harmonik.