img071

71

6.3. Wybór liniowej funkcji przynależności

3)    prosty w realizacji algorytm „uczenia” (ustalania na podstawie ciągu U wartości V’) - patrz p. 6.4;

4)    bezpośredni związek algorytmu z metodą NM\

5)    prosty związek pomiędzy wzorem (58) a zasadami funkcjonowania mózgu człowieka [6).

*2,1

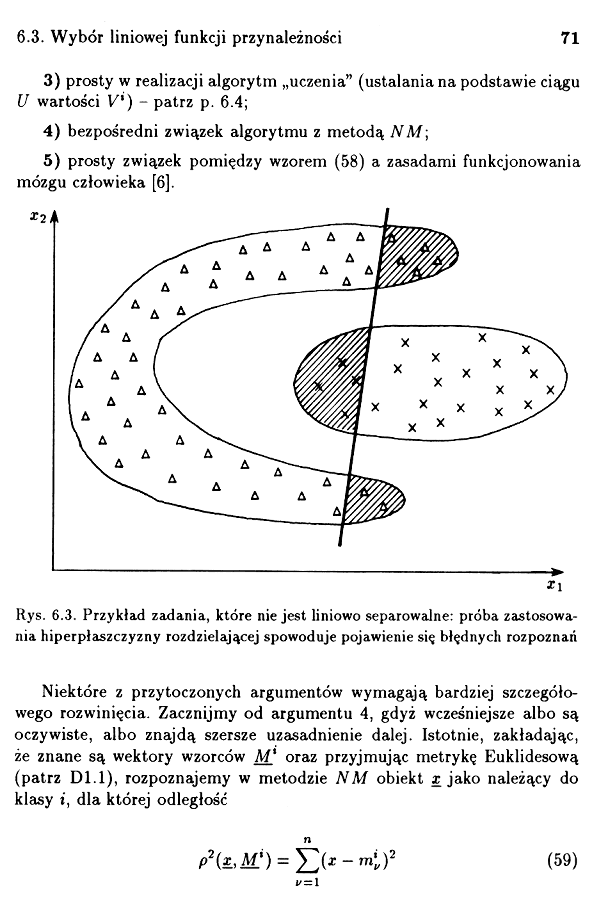
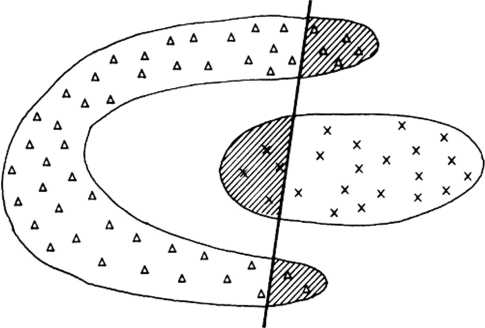
Kys. 6.3. Przykład zadania, które nie jest liniowo separowalne: próba zastosowania hiperplaszczyzny rozdzielającej spowoduje pojawienie się błędnych rozpoznań

Niektóre z przytoczonych argumentów wymagają bardziej szczegółowego rozwinięcia. Zacznijmy od argumentu 4, gdyż wcześniejsze albo są oczywiste, albo znajdą szersze uzasadnienie dalej. Istotnie, zakładając, że znane są wektory wzorców A/' oraz przyjmując metrykę Euklidesową (patrz 01.1), rozpoznajemy w metodzie NM obiekt i jako należący do klasy i, dla której odległość

n

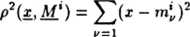
(59)