img087

87

Rozdział 7. Sieć Hopfiehfa

wyjściowych z poszczególnych neuronów we wzorze definiującym łączne pobudzenie ($9 odbywa się po wszystkich elementach i G VJl czyli po wszystkich elementach sieci. Oznacza to, że w sieci przewidziane są także połączenia z warstw dalej położonych (wyjściowych) do warstw wcześniejszycłi — czyli sprzężenia zwrotne.

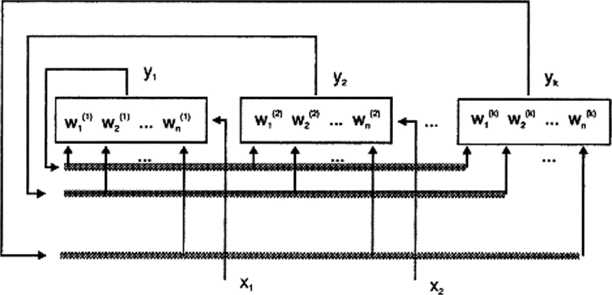
Jak było to wcześniej odnotowane, sieć o takim schemacie połączeń nazywana jest siecią autoasocjacyjną. W ramach tego sprzężenia każdy neuron jest także połączony jednym z wejść ze swoim własnym wyjściem, zatem zasada autoasocjacyjności odnosi się także do pojedynczych neuronów. Każdy neuron sieci ma także kontakt z pewnym, odpowiadającym mu sygnałem wejściowym Xm\ zatem zaciera się tu podział na warstwę wejściową i pozostałe warstwy sieci. Podobnie w związku z zasadą łączenia „każdego z każdym” neurony sieci Hopfielda nie tworzą wcale wyraźnie wydzielonych warstw i mogą być rozważane w dowolnej topologii. My utrzymamy jednak nadal rysunki w formie warstw. Przyjmując, w dalszych rozważaniach najprostszy, jednowarstwowy i jednowymiarowy model sieci otrzymujemy następujący jej schemat:

7.2 Natura procesów w sieciach Hopfielda

Warto zauważyć, że w sieciach autoasocjacyjnych możliwe jest pojawianie się pewnych przebiegów dynamicznych, polegających na tym, że uzyskane w pewnym kroku j wartości sygnałów wyjściowych wszystkich neuronów sieci (ni = 1,2,..., it) stają się automatycznie wartościami wejściowymi    G 97? w kolejnym kroku symulacji. Oznacza to, że sieć

realizuje nieliniowe wektorowe odwzorowanie