img131

131

M [16] pokazano, jak w ogólny* przypadku należy dobierać koóce przedziałów kwantowania    oraz pozioay kwantowania X_A, by zainiaalizować śred-

niokwadratowy błąd kwantowania. Przypadkiea ogólnya żałować się nie będziemy; błąd kwantowania (1.4.5) zainiaalizujeay przy założeniu, że kwantowanie jest gęste (praktycznie dla M > 64) oraz znane są koóce przedziałów kwantowania. To ostatnie założenie jest usprawiedliwione tya, że docelowo interesować nas będzie kwantowanie równoaierne. Ola gęstego kwantowania zależność (1.4.5) aożeay zapisać w postaci

_ M-l *i^l

e² -

E‘iJ

(x - X_iy dx

(1.4.6)

i*0

gdzie jest prawie stałą wartością funkcji gęstości prawdopodobieństwa f(x) w i-tya przedziale kwantowania. Optyaslne pozioay kwantowania aożeay wyznaczyć z układu równań

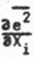
0

(1.4,7a)

i*0,l,2,...,M-1

Po krótkich rachunksch otrzyaujeay

^Xi

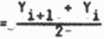
(1.4.7b)

co oznacza, że przy gęstya kwantowaniu pozioay kwantowania powinny być równe współrzędny* środków przedziałów kwantowania. Na rysunku 1.50b przedstawiono charakterystykę statyczną kwantyzatora równomiernego, wynikającą z reguły (1.4.7b).

Hiniaalna wartość błędu kwantowania wynosi (po podstawieniu wartości pozioaów kwantowania (1.4.7b) do określenia błędu kwantowania (1.4.6))

.2

M-l

17 Ś ^Pi ^qi

(1.4.8a)

gdzie p^ m f_iq_i jest prawdopodobieństwea, że sygnał przetwarzany przyjmuje wartość chwilową z i-tego przedziału kwantowania. Z (1.4.8a) wynika, 2e ainiaalna wartość błędu kwantowania wyraża się ważoną średnią kwadratów długości przedziałów kwantowania (zawartych w zakresie zaienności sygnału)