img168

168

r_q<^r²    (1.4.48,)

realizowaną tylko wówczas, gdy przetwornik pracuje na granicy obcinania krzywizny. W modulacji DM długość słowa kodowego m=l, a więc szybkość transmisji R/(2f_g) » r. Korzystając z (1.4.47) otrzymujemy wyrażenie na odstęp sygnał - szum aproksymacji

T_a ś    * —^w’(——    (1.4.48b)

⁰ 2wr    .21 _g

Odstęp sygnał - błąd kwantowania dla modulacji PCK określimy z zależności (l.A.lOb) przy podobnych założeniach (sygnał przetwarzany jest harmoniczny, kwantyzator pracuje na granicy obcinania szczytów

tq ⁼ \ n^{2 =} \ ⁴"    (1.4.498)

H modulacji PCM częstotliwość próbkowania tylko w niewielkim stopniu przewyższa częstotliwość Nyguista r w 1 i wobec tego szybkość transmisji wynosi R/(2fg) = m. Odstęp sygnał - szum aproksymacji wynosi zatem

o

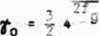
Przebieg zależności (1.4.48b) oraz (1.4.49b) jest przedstawiony na rysunku. 1.63.'

Porówiując zależności (1.4.4Bb) oraz (1.4.49b) wnioskujemy, że powiększenie szybkości transmisji daje znacznie lepsze efekty w modulacji PCM (wzrost wykładniczy) aniżeli w modulacji DM (wzrost potęgowy). Innymi słowy, tę samą wartość odstępu sygnał - szum co w modulacji DM osiągniemy w modulacji PCM przy mniejszej szybkości transmisji. Zwracamy uwagę, że wzrost szybkości transmisji w modulacji PCM przy ustalonej częstotliwości próbkowania wiąże się ze wzrostem długości słowa kodowego i wobec tego wzrostem liczby przedziałów kwantowania , podczas gdy w modulacji DM jest on równoważny wzrostowi częstotliwości próbkowania. Oznacza to, że odstęp sygnał - szum jest bardziej wrażliwy na dyskretyzację wartości sygnału (kwantowanie) niż na dyskretyzację argumentu sygnału (próbkowanie).

Rozważmy teraz modulację PCM oraz DPCM. Odstęp sygnał - błąd kwantowania dla tych rodzajów przetwarzania jest związany zależnością (1.4.39)