img323

Rozkład dwumianowy

Bardzo często mamy do czynienia z doświadczeniem, którego wyniki przybierają zawsze jedną z dwu wzajemnie wykluczających się wartości a prawdopodobieństwa uzyskania tych wyników pozostają te same przez cały czas prób. Zazwyczaj oznaczamy te prawdopodobieństwa przez p oraz ą i wynik o prawdopodobieństwie p nazywamy sukcesem, natomiast wynik o prawdopodobieństwie ą — porażką.

Zachodzi oczywiście:

p + ą = 1 czyli q - 1 - p

Załóżmy teraz, że przeprowadzamy całą serię takich doświadczeń (ścisłej mówiąc powtarzamy doświadczenie n razy). Ponieważ doświadczenia są niezależne, zatem prawdopodobieństwo uzyskania w serii n doświadczeń k pierwszych sukcesów wynosi

p* q(ⁿ *)

Jeśli interesuje nas tylko ogólna liczba sukcesów osiągniętych w wyniku n prób. a nie ich kolejność to prawdopodobieństwo uzyskania k sukcesów w n próbach jest równe

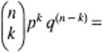
n!

// cf'ⁿ~^k1

Powstały w ten sposób rozkład prawdopodobieństwa nazywa się rozkładem dwumianowym. Zachodzi zatem:

P^k<t

P (X* = k)

k ! (n - k)!

gdzie X" oznacza zmienną losową składającą się z n prób. Rozkład ten zależy zatem od dwóch wielkości: prawdopodobieństwa sukcesu — p, oraz wielkości serii doświadczeń — n.

Rozkład dwumianowy (zwany inaczej rozkładem Bernoulliego) często występuje w praktyce. Przykładowo¹ przypuśćmy, że dla n ludzi zmierzono ciśnienie krwi przed

323

1

Przykład zaczerpnięty z: Fcllcr W.: Wstęp do rachunku prawdopodobieństwa, PWN, Warszawa. 1977